au sommaire
Vie artificielle : l'expression éveille les plus anciens fantasmes de l'humanité. De Prométhée à R. Daneel Olivaw d'Asimov en passant par la créature de Frankenstein, l'Homme s'est toujours interrogé sur sa capacité à créer la vie.

Se familiariser avec le concept de vie artificielle
Ce dossier propose d'exposer de façon complète le concept de vie artificielle. Après un tour d'horizon des considérations historiques et techniques sur la vie artificielle, vous pourrez vous familiariser avec les principes bâtisseurs de cette forme de vie : les algorithmes évolutionnaires, les L-systèmes, les essaims de particules, les machines autoréplicatrices, l'intelligenceintelligence collective...

À lire aussi sur Futura :
- Vie artificielle : quel avenir ?
- Le secret des fourmis pour éviter les embouteillages
- Jeu mathématique : quel est le trajet optimal d'un voyageur de commerce ?
- Le hasard existe-t-il ?
- Bio-inspirations, fractales, complexité et émergence
Création de la vie et philosophie : Descartes, Darwin, Langton…
Durant l'essentiel de l'histoire de l'humanité, la vie a été considérée comme le propre de Dieu. Lorsque les premiers scientifiques et penseurs ont exprimé la possibilité de créer la vie de façon artificielle, cela n'a pas été simple...
Seul le démiurge peut donner la vie ; la génération spontanée, phénomène longtemps perçu comme hautement banal, n'était alors que l'expression du pouvoir créateur de Celui qui est à l'origine de tout.
La création de la vie selon Lamarck, Darwin et Descartes
À partir du XVIIe siècle, principalement sous l'impulsion des philosophes français, une nouvelle vision de la vie a progressivement émergé :
- « Ceux qui connaissent les automatesautomates considéreront le corps comme une machine qui, ayant été faite des mains de Dieu, est incomparablement mieux ordonnée, et a en soi des mouvements plus admirables, qu'aucune de celles qui peuvent être inventées par les Hommes... s'il y avait de telles machines qui eussent les organes et la figure d'un singe ou de quelque autre animal sans raison, nous n'aurions aucun moyen pour reconnaître qu'elles ne seraient pas en tout de même nature que ces animaux [...] ». (Descartes R., Le Discours de la méthode, Paris, Librio, 1999.))
Selon Descartes, la vie peut ainsi s'interpréter comme un mécanisme, seule l'âme - siège de la raison - relève alors du divin (dualisme).
De même, l'idée de structures vivantes fixes, créées une fois pour toutes, a reculé au profit d'une interprétation transformiste puis évolutionniste. Les travaux de Lamarck, puis de DarwinDarwin, ont ainsi définitivement sonné le glas de la vision antique du vivant.
Malgré ces progrès, les Hommes de science ont, dans leur immense majorité, continué de penser que la création de la vie nous restait inaccessible. Seuls certains écrivains, comme Mary ShelleyMary Shelley avec Frankenstein, osaient poser la possibilité pour l'Homme d'égaler Dieu.
Vers la vie artificielle : Christopher Gale Langton
La révolution scientifique du XXe siècle a bousculé ces interprétations. L'idée a progressivement émergé que la vie, considérée comme un mécanisme, comme un processus, pouvait être à la portée de la connaissance humaine.
En 1987 s'est tenue à Santa Fe, au Nouveau-Mexique (États-Unis), la première conférence internationale sur la vie artificielle. Son jeune organisateur Christopher LangtonChristopher Langton déclarait alors en prélude :
- « La vie artificielle est l'étude des systèmes construits de mains d'Hommes qui exhibent des comportements caractéristiques des systèmes naturels vivants. Elle vient en complément des sciences biologiques traditionnelles qui analysent les organismes vivants, en tentant de synthétiser des comportements semblables au vivant au sein d'ordinateursordinateurs et d'autres substratssubstrats artificiels. En étendant les fondements empiriques sur lesquels la biologie est basée au-delà de la vie à base de carbone qui a évolué sur Terre, la vie artificielle peut contribuer à la biologie théorique en positionnant la vie telle que nous la connaissons au sein d'un espace plus large : la vie telle qu'elle pourrait être. » (Langton C. G., Artificial Life I, Addison-Wesley, 1989, p. 1, italiques originales).
Le concept de machine universelle : les machines de Turing
Créer la vie, de façon artificielle, est devenu le défi de tout savant. Comment Langton et Turing ont-ils marqué l'histoire de la vie artificielle ? Qu'est-ce qu'une machine universelle ?

L'objectif de Langton était ambitieux :
- « Le but ultime de la vie artificielle serait de créer la "vie" dans un autre substrat, idéalement un substrat virtuel où l'essence de la vie aurait été abstraite des détails de sa mise en œuvre dans quelque substrat que ce soit. Nous aimerions construire des modèles qui sont si semblables au vivant qu'ils cesseraient d'être des simulations de la vie pour en devenir des exemples. » (Langton C. G., « Studying Artificial Life with Cellular Automata », Physica D, 22, 1986, p. 147, italiques originales.)
Cette citation illustre ce que l'on qualifie maintenant d'interprétation forte de la vie artificielle. Comment Langton a-tt-il pu conclure à la faisabilité d'un tel programme ? Ceci apparaît d'autant plus difficile qu'à ce jour, nous ne disposons toujours pas d'une définition incontestée de la vie. C'est donc d'abord un problème philosophique qu'il posait.
Pour Langton, la vie est une affaire d'organisation et de structure, non de substance. Dans ce contexte, la possibilité théorique existerait de réaliser de nouvelles instances du vivant. Son raisonnement trouve ses racines dans les travaux des grands logiciens de la première moitié du XXe siècle avec en particulier Alonzo Church et Alan TuringAlan Turing.

Alan Turing et le concept de machine universelle
En 1936, Alan Turing a proposé le concept de machine universelle. Il montrait alors comment un système logique minimum permettait de déterminer toutes fonctions calculables. Ce travail, qui est à l'origine de l'ordinateur (votre PCPC n'est rien d'autre qu'une machine universelle de Turing finie), a donné lieu à la thèse de Church-Turing.
Une machine de Turing, un modèle abstrait aux applications multiples
Dans sa version de base, elle énonce que toute fonction calculable l'est par une machine de Turing. Cette thèse a été élargie dans ce que l'on qualifie de « version physique » selon laquelle une machine de Turing peut réaliser toute opération de traitement de l'information réalisable par un système physique.
L'interprétation faible de cette thèse pose ainsi que tout système pouvant être décrit comme un automate peut être simulé par une machine de Turing. Selon l'interprétation forte, une machine de Turing peut reproduire le comportement de tout système physique. Douglas Hofstadter a parlé de « version microscopique » :
- « Le comportement des éléments constitutifs d'un être vivant peut être simulé par un ordinateur. Autrement dit, une description suffisamment élaborée de l'état interne et de l'environnement local de n'importe quel élément (on suppose généralement qu'il s'agit d'une cellule) permet de faire calculer son comportement de façon arbitrairement précise par... une fonction récursive générale. » (Hofstadter D., Gödel, Escher, Bach, Dunod, Paris, 1999, p. 641. Church a montré que les fonctions calculables sont les fonctions récursives).
L’intelligence artificielle vise à mimer le fonctionnement du cerveau humain, ou du moins sa logique lorsqu’il s’agit de prendre des décisions. Futura est parti à la rencontre de Jean-Claude Heudin, directeur du laboratoire de recherche de l’IIM (Institut de l’Internet et du multimédia) afin de mieux comprendre d’où vient ce concept. © Futura
Machines universelles finies et intelligence artificielle
Les ordinateurs, c'est-à-dire des machines universelles de Turing finies, sont capables de traiter tout algorithme fini. Si on leur fournit la description logique d'une machine, c'est-à-dire les déterminants de son organisation, ils seraient capables de la « réaliser ». On arrive ainsi à l'idée selon laquelle « les ordinateurs sont des instances des processus biologiques ». Cette thèse relève de l'option philosophique. Pour être admise, elle suppose que l'on accepte que la réalité d'un système relève strictement de son organisation et qu'elle est donc indépendante de son support physique, c'est ce que l'on appelle « le fonctionnalisme ».
Trouvant son origine dans l'intelligence artificielle, il pose ainsi qu'il serait possible de reconstruire la logique d'un cerveau humain en dehors du substrat neuronal. La vie est affaire d'organisation et non de substance ; tout fait organisationnel physique ou non est réalisable par une machine de Turing. Ces deux assertions, profondément discutables l'une comme l'autre, sont au cœur de l'interprétation forte de la vie artificielle.
Thomas Ray et le programme Tierra : l'ambition créatrice
Certains affirment avoir créé de nouvelles formes de vie. Le plus célèbre d'entre eux - Thomas Ray - est à la base du programme Tierra présentant un univers virtuelunivers virtuel.

Thomas Ray a écrit un article intitulé « Comment j'ai créé la vie dans un univers virtuel » (Ray T.-S., How I Created Life in a Virtual Universe, 1993).
On pourrait penser qu'il s'agit là de l'une de ces envolées lyriques que l'on rencontre parfois chez les théoriciens de l'informatique, mais Ray est d'abord un biologiste. Spécialiste de la forêt tropicale, il a consacré toute la première partie de sa carrière à la biologie, ce n'est que plus tard qu'il est venu à l'informatique. Comment un biologiste a-t-il pu aboutir à une telle conclusion ?

L'univers virtuel de Tierra
Ray a construit un programme (Tierra) qui représente un univers virtuel. L'espace y est formé par la mémoire électronique, la matière par des « instructions processeurs ». Ces instructions sont vues comme les molécules « chimiquement actives » de cet univers virtuel. Par leur capacité à se déplacer au sein de l'espace, à se transformer ou à s'associer à d'autres « molécules », elles constituent une forme de matière programmable (on parle alors de chimiechimie artificielle).
Ray a construit une « créature » formée d'un ensemble d'instructions (baptisé « l'Ancêtre »), ayant la capacité de se reproduire, c'est-à-dire de se répliquer en un point donné de l'espace mémoire. Par analogieanalogie avec la biologie, les mécanismes de réplicationréplication et d'exécution des instructions étaient « brouillés », des modifications aléatoires (l'équivalent des mutations) pouvaient par exemple se produire.
Le parasitisme de Tierra : de nouveaux êtres vivants ?
Très rapidement, Ray a vu apparaître des « individus » autoréplicateurs d'un nouveau genre. Très courts, ils ne disposaient pas des instructions de réplication, mais utilisaient celles d'ancêtres se trouvant dans leur voisinage. Le parasitisme est ainsi apparu spontanément au sein de Tierra. Plus tard sont advenus des individus immunisés, puis toute une faunefaune de parasitesparasites et d'hyperparasites (des individus détournant les parasites à leur propre profit). Des mécanismes jusque-là considérés comme le propre du vivant ont ainsi émergé au sein de l'univers virtuel de Tierra.
Pour Ray, peut être considérée comme vivante toute structure autoréplicatrice capable d'une « évolution ouverte » ; ce serait le cas des créatures de Tierra qui représenteraient donc une nouvelle instance du vivant, une forme de vie totalement originale. Cette définition est pour le moins hasardeuse et la notion de parasitisme dans Tierra est sujette à caution. Cette constructionconstruction n'en est pas moins remarquable par sa capacité à montrer l'émergenceémergence « spontanée » de processus apparemment propres au vivant.

Les algorithmes évolutionnaires, un exemple de vie artificielle
Par leurs implications philosophiques, les tentatives de re-création de la vie illustrent le côté le plus fascinant de la vie artificielle. Dans la pratique, ces travaux sont pourtant loin d'être les plus importants, ni les plus représentatifs de la « discipline ». Zoom sur les algorithmes évolutionnaires.

La vie artificielle ne se limite pas aux seules tentatives de construction de nouvelles instances de la vie ou à la biologie théorique. Elle s'inspire des propriétés du vivant pour proposer des constructions originales, tant algorithmiquesalgorithmiques que physiques, dotées de capacités étonnantes et aptes à résoudre des problèmes difficiles vis-à-vis desquels les approches plus traditionnelles rencontrent de graves difficultés. C'est le vaste domaine des artefacts biomimétiquesbiomimétiques (algorithmiques et robotiquesrobotiques).
Naissance des algorithmes évolutionnaires
Les biologistes utilisent le concept de paysages adaptatifs pour représenter l'ensemble des combinaisons génétiquesgénétiques et les niveaux d'adaptation correspondants. Par exemple, dans un diagramme en trois dimensions, la hauteur (z) représente le niveau d'adaptation de l'ensemble des configurations génétiques (x, y).
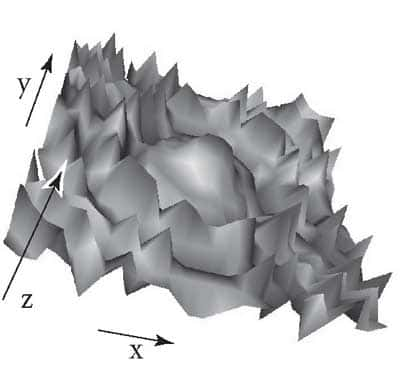
Les mécanismes évolutifs ont montré leur efficacité, leur capacité à rejoindre les points les plus « élevés » des différents paysages adaptatifs. C'est cette capacité qui a inspiré les chercheurs en informatique qui en ont pris modèle pour proposer des algorithmes originaux. Cette branche de la science informatique est devenue l'algorithmique évolutionnaire.
Principe des algorithmes évolutionnaires : les populations
De nombreux problèmes d'optimisation (classiquement non linéaires) ou de recherches au sein de vastes espaces (explosion combinatoire) n'ont pas de « solutions mathématiques » directes. Des méthodes très diverses ont été proposées qui vont de l'exploration systématique à l'exploration aléatoire. Les plus récentes utilisent souvent le « hasard guidé », c'est-à-dire qu'à des procédures plus ou moins empiriques sont associées des procédures aléatoires permettant de sortir des optima locaux. On a proposé ainsi d'utiliser des mécanismes s'inspirant directement de la théorie darwinienne. L'idée consiste tout simplement à construire une « population » aléatoire de solutions potentielles au problème posé. Les « individus » sont ensuite testés (calcul de la fitnessfitness) afin de favoriser la « reproduction » des plus aptes, c'est-à-dire ici de ceux qui s'approchent le plus de la solution. Les mécanismes de reproduction, de croisement des individus les plus adaptés et de mutations permettent progressivement d'approcher la solution recherchée.
Par exemple, pour résoudre le fameux problème du voyageur de commerce (il s'agit de trouver le chemin le plus court pour relier un certain nombre de villes). Malgré son apparente simplicité, il s'agit là d'un exemple classique de ces problèmes dits « NP » (dont la complexité croît plus vite que n'importe quelle puissance de la variable), qui posent des questions fondamentales à l'informatique théorique. On construit une population représentant un ensemble de parcours aléatoires. On sélectionne ensuite les meilleurs (les plus courts) que l'on croise entre eux pour obtenir une nouvelle population de parcours et ceci aussi longtemps qu'on le souhaite pour approcher le parcours optimum. Les résultats obtenus montrent que les algorithmes évolutionnaires sont particulièrement adaptés à ce type de problème.
Domaines d'application des algorithmes évolutionnaires
Les algorithmes évolutionnaires ont maintenant fait leurs preuves. On les retrouve par exemple dans des domaines aussi divers que l'industrie (optimisation des allocations de ressources, programmation de robots...), la conception (optimisation de formes...) ou encore la bourse. Plus encore, des environnements de programmation dédiés, destinés à faciliter l'appropriation de ces méthodes par les non-spécialistes, sont en cours de développement, notamment en France avec le langage EASEA de Pierre ColletCollet (Collet P., Lutton E. et al., « Take it EASEA », Parallel Problem Solving from Nature VI, vol. 1917, Paris, Springer, 09/2000, p. 891-901.). En 2010 par exemple, l'équipe de Pierre Collet a participé aux 20e Journées évolutionnaires à Paris VI.
Les L-systèmes pour comprendre la morphogenèse
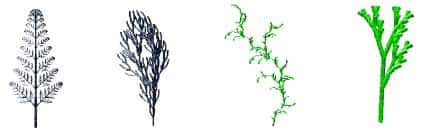
Les processus de la morphogenèsemorphogenèse restent mystérieux. Malgré les progrès de la génétique, de nombreux mécanismes nous restent inconnus. A. Lindenmayer (1925-1989) a proposé une méthode de description formelle de la structuration des plantes : les L-systèmes.

Basée sur une forme récursive de grammaire générative, la méthode de Lindenmayer a été approfondie et mise en œuvre graphiquement par P. Prunsinkiewciz dans les années 1980.

Les procédures utilisées sont simples, mais nous ne les décrirons pas ici. Contentons-nous de présenter quelques-unes des images obtenues. Ces figures ont été réalisées avec L-System 4 de T. Perz.
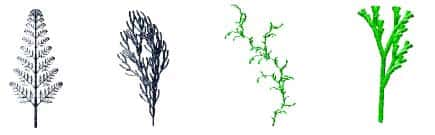

Plantes et L-systèmes
L'inspiration biomimétique de ces figures est indéniable. Elles ne sont pourtant que l'interprétation graphique de chaînes de caractères construites à partir d'un algorithme récursif.
Il est très difficile de cerner le lien entre la morphogenèse végétale et les L-systèmes. De même que les paysages engendrés par les fractales, malgré leur ressemblance avec la réalité, n'ont en aucune manière suivi une évolution comparable aux paysages naturels, les similitudes entre plantes et L-systèmes ne signifient nullement que les génomesgénomes végétaux décrivent un mécanisme identique. Les L-systèmes n'en confortent pas moins l'hypothèse selon laquelle les processus morphogénétiques mettent en œuvre des procédures répétitives, probablement souvent récursives.
Voir aussi notre page de dossier L-systems : les chaînes de Lindenmayer.
Vie artificielle et inspiration de la nature : les essaims de particules
Parmi les systèmes de vie artificielle inspirés de la nature, se trouvent les essaims de particules.

Craig Reynolds et les principes des algorithmes d'optimisation par essaim de particules
Les algorithmes « d'optimisation par essaim de particules » (Particle Swarm Optimization - PSO) trouvent leur origine dans les boids de l'infographiste Craig Reynolds (Reynolds explique et montre son algorithme ici : analysant les nuées d'oiseaux, Reynolds a proposé de les simuler à partir de trois règles simples d'applicationapplication locale : http://http://www.red3d.com/cwr/boids/) :
- Chaque individu doit éviter de heurter ses voisins ;
- Chaque individu tend à s'approcher des vitessesvitesses et directions générales du groupe localgroupe local, c'est-à-dire des voisins immédiats ;
- Chaque individu cherche à s'approcher du centre de gravitégravité du groupe local.

Il est possible d'y ajouter une règle de propension à rejoindre un point donné dans l'espace (« perchoir »). L'application de ces règles simples a permis de construire des simulations graphiques d'un réalismeréalisme étonnant. Des algorithmes de ce type ont été utilisés dans des films aussi célèbres que Le retour de Batman ou Le Bossu de Notre Dame.
Les rassemblements animaux présentent divers avantages adaptatifs relevant au moins pour partie de l'échange d'informations. De la même manière que les algorithmes évolutionnaires s'inspirent des mécanismes évolutifs pour mettre en œuvre des procédures d'optimisation, PSO s'inspire des phénomènes de rassemblement et de nuée, considérant qu'en tant que processus adaptatifs, ils sont potentiellement porteurs de capacités d'optimisation. PSO repose sur deux règles simples :
- Chaque individu se souvient du meilleur point (le plus proche de l'objectif) par lequel il est passé au cours de ses évolutions et tend à y retourner ;
- Chaque individu est informé du meilleur point connu au sein de la population prise dans son ensemble et tend à s'y rendre.
Essaim de particules et réseau de neurones
L'une des premières applications a été l'entraînement d'un réseau de neurones devant réaliser la fonction booléenne Xor (ou exclusif) et utilisant treize paramètres. L'essaim devait ainsi se déplacer au sein d'un hyperespace à treize dimensions. Chacune de ces dimensions représente alors l'espace des poids possibles pour une connexion neurale donnée.
Cette méthode a maintenant de nombreuses utilisations. On la retrouve comme alternative aux méthodes classiques d'entraînement des réseaux de neurones, mais aussi par exemple dans des procédures d'optimisation de l'alimentation de cultures bactériennes. Là encore, l'utilisation des mécanismes du vivant s'est avérée d'une féconditéfécondité remarquable.
Intelligence collective : l'optimisation par colonie de fourmis
La capacité des insectesinsectes sociaux à réaliser des tâches hautement complexes a également inspiré les informaticiens et donné lieu au concept d'intelligence collective articulé autour des mécanismes d'auto-organisation. L'optimisation par colonie de fourmisfourmis n'est qu'une des nombreuses applications de ce domaine.


Le modèle des fourmis : Deneubourg et Dorigo
J.-L. Deneubourg, de l'université libre de Bruxelles, a proposé une explication des capacités d'optimisation des procédures de recueil de ressources chez certaines espèces de fourmis. Très schématiquement, au départ un grand nombre de fourmis se déplacent à l'extérieur du nid, plus ou moins au hasard à la recherche de nourriture. Quand elle découvre une ressource, une fourmi rentre au nid en déposant une trace de phéromonesphéromones. Cette trace tend à attirer les congénères qui, en la suivant, vont parvenir à la nourriture. Ils vont alors retourner au nid et renforcer la trace à leur tour.
On assiste ainsi à la mise en place d'une boucle de rétroactionboucle de rétroaction positive (« effet boule de neige »). S'il existe plusieurs chemins pour atteindre la ressource, l'accumulation de phéromones sera nécessairement plus rapide sur le chemin le plus court. C'est ainsi que certaines espècesespèces de fourmis tendent à optimiser le recueil de nourriture.
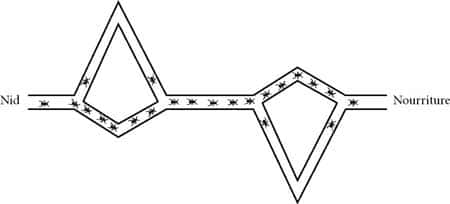
Marco Dorigo s'est appuyé précisément sur ce mécanisme pour proposer l'approche dite « optimisation par colonie de fourmis » (Ant Colony Optimization) qu'il a d'abord validée en l'appliquant au problème du voyageur de commerce. On trouve maintenant des « fourmis » dans le routageroutage des télécommunications, l'allocation des ressources dans les processus industriels ou encore la conception de circuits électroniques.
Machines autoréparables et composants FPGA
Au fur et à mesure des recherches et des expériences, le développement de la vie artificielle a fait des progrès. L'utilisation d'éléments FPGAFPGA (des composants électroniques reprogrammables) a permis de concevoir des machines d'un nouveau genre, en ce sens qu'elles sont capables de s'autoréparer.

Le LSL de Lausanne, sous la direction de Daniel Mange, est particulièrement en pointe dans le domaine des machines capables de s'autoréparer.
BioWatch, une horloge à base de composants FPGA
On y a construit par exemple la BioWatch, une horloge conçue à base de composants FPGA, qui est capable de se reconfigurer d'elle-même en cas de défaillance de l'un ou l'autre de ses composants. En cas de défaillance grave, elle est même capable de se dupliquer au sein d'autres composants afin de pérenniser son fonctionnement.
Plus récemment, le LSL a conçu le BioWall, un système qui préfigure aussi bien de nouvelles interfaces tactiles, qu'un futur tableau noir ou que les tissus intelligents de demain.

Les mécanismes mis en jeu dans ces systèmes pourront fournir les bases de nouvelles machines robustes, aptes à s'adapter à la tâche en cours et à « survivre » dans un environnement difficile et changeant (on pense en particulier à l'exploration spatiale). Associés aux nanotechnologies, ils pourraient permettre des réalisations dignes de la plus ébouriffante des sciences-fictions.
Biomimétisme, robots et animats
Les roboticiens s'inspirent du vivant. Toute une branche de la recherche s'appuie sur la construction de robotsrobots simples, dotés de quelques capacités élémentaires inspirés du comportement animal. C'est le vaste domaine des animatsanimats.

On note qu'on utilise fréquemment des algorithmes évolutionnaires pour programmer les robots animats (robotique évolutionnaire).

L'inspiration biomimétique : enjeux et difficultés
De même, on s'inspire des travaux sur les insectes sociaux pour construire des systèmes composés d'un ensemble de robots simples dont les interactions permettent de réaliser des tâches plus ou moins complexes. On parvient ainsi, par exemple, à faire déplacer des objets trop lourds pour un individu seul, ou à amener un groupe de robots à trier des objets.
Il est important de comprendre ici, que ces résultats sont obtenus sans coordination centrale et avec des machines dotées de capacités extrêmement simples. On peut espérer ainsi obtenir des systèmes de faible coût et d'une très grande robustesse dans la mesure où la destruction de quelques individus n'empêche nullement la réalisation de la tâche assignée.

On pourrait multiplier ainsi les exemples à l'infini, mais tous montrent que l'utilisation des mécanismes du vivant au sein d'algorithmes ou de robots ouvre une voie originale aux développements technologiques du XXIe siècle.
Il est toutefois nécessaire de tempérer l'enthousiasme que pourraient susciter ces créations. La nature n'est pas avare, elle dispose de ressources quasiment illimitées et ne mesure pas son temps. L'évolution darwinienne n'a pas d'objectif et les formes de vie que l'on connaît sont le résultat tant de la contingence que d'une infinité de tâtonnements, d'une infinité d'essais et d'erreurs. De même, il est très simple de concevoir des systèmes de recueil de ressources ou de construction d'un nid qui soient immensément plus efficaces que ceux que l'on trouve chez les insectes sociaux. Là encore, la nature n'est pas avare de ses ressources.
Plus encore, il est très difficile de contrôler les résultats obtenus. Par exemple, en voulant programmer un robot devant se déplacer le plus loin possible en évitant les obstacles, on a pu obtenir une machine qui se contentait de tourner sur elle-même (ce qui n'était évidemment pas l'objectif), ses roues faisaient ainsi un très grand nombre de tours (ce qui était interprété comme un déplacement long) et le robot ne heurtait jamais d'obstacles.
La biomimétique pour le futur
Les systèmes biomimétiques permettent de résoudre des problèmes difficiles, les résultats sont généralement d'une robustesse exceptionnelle et les mécanismes utilisés sont d'une souplesse que l'on ne rencontre que très rarement dans les réalisations plus traditionnelles.
En ce sens, l'inspiration biomimétique est un outil nouveau, extrêmement puissant, qui vient compléter la palette de ceux dont disposent les chercheurs et les ingénieurs.