au sommaire
Comment se peut-il que les plantes marquent une prédilection pour la suite de Fibonacci ou pour le nombre d'or ? Le nombre d'or apparaît plus directement dans la géométrie des hélices ou des spirales. Peut-on imaginer que ce fameux nombre d'or soit présent dans leur génomegénome.
Et, si c'était le cas, y a-t-il là un souci esthétique comme l'exemple des beaux-arts pourrait le faire penser ? Cette dernière question n'est pas si absurde qu'il y paraît. Après tout, les splendides coloris des fleurs ont pour effet d'attirer les abeilles ou autres transporteurs de pollenpollen, ce qui favorise la reproduction de ces mêmes plantes. Les arrangements spiralés de la marguerite ou du tournesoltournesol auraient-ils une fonction équivalente ? Et si l'esthétique n'y est pour rien, c'est-à-dire si les abeilles ne sont pas particulièrement sensibles à la magie du nombre d'or, ne peut-on trouver dans ces arrangements un avantage quelconque qui permettrait de comprendre que la sélection naturellesélection naturelle les ait favorisés ?

Dans le passé, les naturalistes ont imaginé quelques explications qui attribuaient un avantage évolutif à des arrangements associés au nombre d'or. Aujourd'hui, nous n'y croyons plus. Nous ne pensons pas que le nombre d'or soit inscrit dans le génome. Une image simple permettra peut-être d'exposer la position actuelle.
Nous admirons la bulle de savon irisée avec laquelle joue la petite fille. Cette forme sphérique, cette légèreté, ces couleurs chatoyantes, cette fragilité même nous fascinent. Nous savons tous que les atomes se combinent pour former des molécules qui, à leur tour, constituent les solidessolides ou les liquidesliquides, les cailloux comme les bulles de savon.
La nature utilise un minimum de matière
Pourquoi les bulles sont-elles sphériques (et non cubiques, par exemple) ? Ce qui importe ici, c'est de savoir que la réponse à cette question ne fait pas appel aux lois très complexes qui régissent le mouvementmouvement des électronsélectrons dans les atomes. La réponse complète, qu'il n'est pas nécessaire de donner ici, découle d'un théorèmethéorème simple de la géométrie euclidienne.
Ce théorème s'énonce à peu près ainsi : dans notre espace à trois dimensions, c'est la sphère qui, parmi toutes les surfaces enfermant le même volumevolume, a la superficie la plus faible. Imaginons un enfant qui dispose d'un grand nombre de cubes de pâte à modeler de tailles identiques. Avec chacun des blocs il sculpte une figurine différente : une boule, un canard, un dé, un chat. S'il décide de recouvrir chacune de ces sculptures d'une couche de peinture de même épaisseur, il pourra vérifier que c'est la boule qui va le moins entamer sa réserve de couleur.
Dans tout ceci, il n'a pas été question de la composition chimique des bulles ni de la nature des forces entre molécules (ou, ce qui revient au même, entre cortèges électroniques). Cette sphéricité des bulles a un caractère universel (les petites gouttes de mercuremercure liquide, par exemple, prennent également la forme d'une sphère).
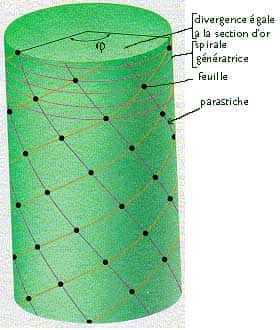
La suite de Fibonacci dans le monde végétal
L'émergenceémergence de la suite de Fibonacci chez les plantes est un phénomène parfaitement analogue. La structure du génome n'y joue pas un rôle plus important que celui de la structure atomique dans l'apparition de la forme sphérique des bulles. Cette remarque permet de comprendre la présence du nombre d'or chez des plantes très différentes : c'est aussi à la géométrie qu'il faut recourir afin de savoir pourquoi la fameuse suite se glisse si régulièrement dans les arrangements spiralés. Il convient cependant de noter que la relation à établir est loin d'être simple. Ce n'est qu'aujourd'hui que l'on possède une vue d'ensemble de ce problème.