Jeu mathématique : quel est le trajet optimal d'un voyageur de commerce ?

Quel trajet doit suivre le voyageur de commerce pour minimiser la distance parcourue ? On peut déterminer le nombre de trajets possibles assez facilement. Pour cela, on choisit une ville que l'on considère comme la ville de départ. Ensuite, on a neuf choix possibles pour continuer, huit une fois ce choix fait, etc. On obtient ainsi 9 x 8 x 7 x... x 1 trajets possibles.

Un trajet entre dix villes. © Hervé Lehning. Tous droits réservés

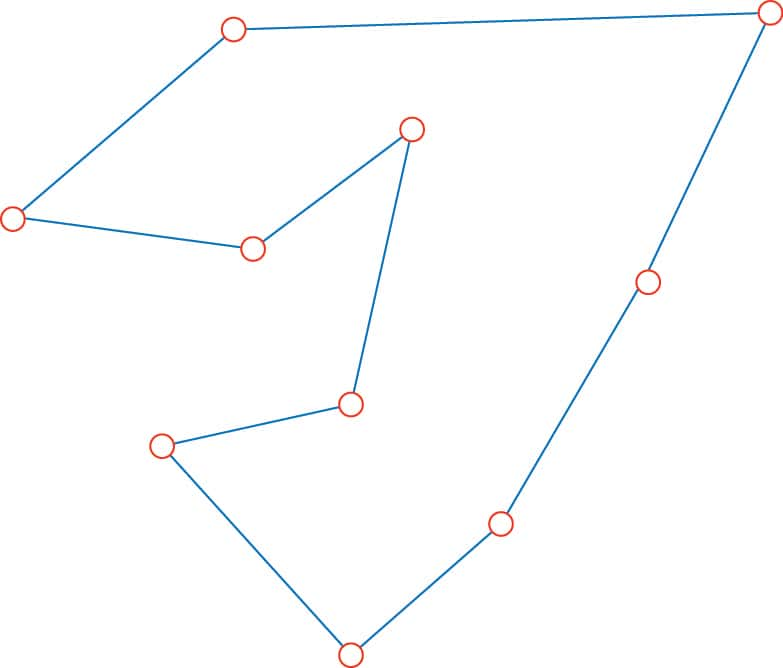
Comme le sens de parcours ne compte pas, le nombre de trajets possibles est 9 x 8 x 7 x 6 x 5 x 4 x 3 = 181.440. Comparer leurs longueurs est donc faisable à l'aide d'un ordinateurordinateur dans le cas de dix villes.

Question :

L’algorithme résolvant le problème du voyageur de commerce présenté ci-dessus est considéré comme inefficace. Pourquoi ?

Réponse :

Le trajet du voyageur de commerce. © Free-photos, Pixabay, DP

Cet algorithme est inefficace car, quand le nombre de villes augmente, il devient vite inapplicable. Par exemple, pour 20 villes, le nombre de trajets à comparer est égal à 60.822.550.204.416.000 ! Si chaque trajet est engendré en une nanoseconde, il faut 60 millions de secondes pour tous les générer tous, ce qui fait environ deux ans. Ainsi, pour 21 villes, il faudra 42 ans, et pour 22, presqu'un millénaire !

Ce problème du voyageur de commerce fait partie d'une classe de problèmes qui pourraient être résolus si l'un des problèmes à un million de dollars de l'Institut Clay était résolu par l'affirmative. Il s'agit de la conjecture « P = NP ».