au sommaire
Instabilité et radioactivité
C'est un principe général de physique que tout système tend à minimiser son énergie. A priori, il n'est donc pas très surprenant de voir la transmutation d'un noyau en un autre si cela conduit à minimiser l'énergie totale. Mais alors pourquoi ne sont-ils pas tous radioactifs, pourquoi l'univers n'est-il pas seulement composé de fer ? Parce qu'il ne suffit pas que les niveaux d'énergie soient dans le bon sens pour permettre une transition spontanée, encore faut-il qu'il n'y ait pas de barrière infranchissable entre les deux niveaux, et que le temps nécessaire à la transition ne soit pas trop long !
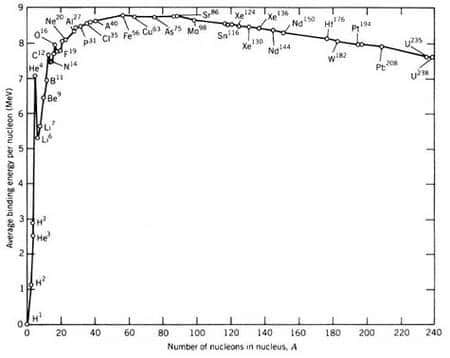
Prenons par exemple un noyau lourd comme l'uraniumuranium 238 (Z=92). La courbe d'Aston indique que l'énergie de liaison par nucléonnucléon diminue au delà du fer, essentiellement en raison de la répulsion électrostatiqueélectrostatique grandissante. Il devient donc peu à peu énergétiquement favorable d'avoir deux noyaux au lieu d'un, par exemple un noyau de baryumbaryum (Z=56) et un de kryptonkrypton (Z=36).
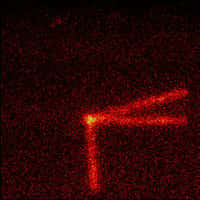
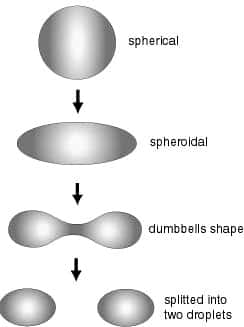
C'est une fissionfission spontanée du noyau. Mais cela exige que le noyau plus ou moins sphérique d'uranium (forme qui assure qu'un maximum de nucléons soit à l'intérieur plutôt qu'en surface) se déforme d'abord en une sorte de haltère avant de se scinder en deux.

Fission spontanée d’un noyau lourd en deux noyaux légers © Kenjiro Takada, Kyushu university
Mais la surface augmente alors fortement, ce qui implique que l'énergie est plus grande dans l'étape intermédiaire. Autrement dit, il y a une barrière énergétique qui s'oppose à cette fission spontanée, barrière que l'on peut franchir en apportant de l'énergie au noyau initial, par exemple en le bombardant de neutronsneutrons. Cette fission induite est utilisée dans les réacteurs nucléaires (l'énergie libérée par la fission est supérieure à celle des neutrons).
La mécanique quantiquemécanique quantique autorise une autre échappatoire, l'effet tunneleffet tunnel. Il est possible à une particule de franchir une barrière d'énergie entre deux états, mais la probabilité de la franchir diminue exponentiellement avec la hauteur et l'épaisseur de la barrière. L'uranium 238 peut donc spontanément fissionner, mais avec une probabilité extrêmement faible.
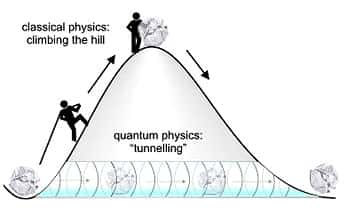
Représentation schématique de l’effet tunnel © F. Krausz (Max-Planck Institut für Quantenoptik)
Il est rare qu'un noyau lourd se scinde spontanément en deux noyaux de taille comparable, il est bien plus « intéressant » d'exploiter la cohésion très forte du noyau d'héliumhélium (souvenons-nous du pic sur la courbe d'Aston) en scindant le noyau lourd en un noyau juste un peu plus léger et un noyau d'hélium. La barrière est moins infranchissable et donc le processus plus probable.
C'est précisément ce que BecquerelBecquerel a découvert en 1896, sans bien sûr comprendre ce dont il s'agissait : l'uranium émet spontanément un rayonnement, baptisé alpha en 1899 par Rutherford qui démontra en 1908 qu'il s'agissait de noyaux d'hélium. La conservation de l'énergie implique que l'alpha emporte une énergie cinétiqueénergie cinétique bien précise, caractéristique de la transmutation. Plus cette énergie est grande, plus son émissionémission (évasion) est probable.
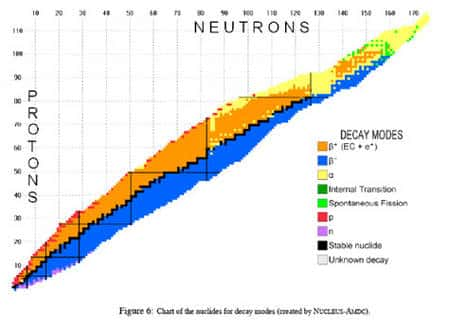
Carte des noyaux connus, la couleur indiquant leur type de radioactivité © Nubase
Cette carte des modes de transmutation des noyaux indique en vert clair les noyaux susceptibles de fission spontanée et en jaune ceux qui émettent plutôt des alphas (les deux modes peuvent bien sûr être simultanément possibles, comme pour l'uranium 238). Ces deux modes ne concernent que les noyaux les plus lourds, la plupart des autres transmutations impliquent des transitions bêtabêta (vocable aussi dû à Rutherford). De quoi s'agit-il ?
La vallée de stabilité a une forme parabolique : pour un nombre donné A de nucléons, il existe une valeur optimale du nombre Z de protonsprotons (et donc N=A-Z de neutrons) qui minimise l'énergie du noyau. Les noyaux qui ont un excédent de neutrons par rapport à cette valeur optimale ont donc « intérêt » à convertir un neutron en proton pour se rapprocher du fond de la vallée. Cette conversion est presque toujours moins coûteuse en énergie que l'expulsion pure et simple d'un neutron, qui coûterait la dizaine de MeV de son énergie de liaison. Mais la conservation de la charge électrique implique de compenser la charge positive du proton créé par une charge négative égale. Il n'y a pas le choix : il faut qu'un électronélectron soit créé en même temps que le proton. Cela coûte d'entrée les 0.511 MeV de sa massemasse, mais le proton est heureusement plus léger de 1.3 MeV que le neutron. De plus l'électron ne peut pas être créé sans création simultanée d'un antineutrino (de masse négligeable). Mais surtout la transformation d'un neutron en proton n'est possible ni par interaction nucléaire forte (elle colle les nucléons entre eux, mais ne les modifie pas) ni par interaction électromagnétique.
Il faut donc supposer l'existence d'une nouvelle interaction, dite interaction faibleinteraction faible (les physiciensphysiciens nucléaires ne manquent pas d'imagination). Enrico FermiEnrico Fermi en a donné dès 1934 un première formulation, remaniée ensuite sous la forme de l'émission d'un bosonboson W par le neutron (qui devient alors un proton), le W se transformant ensuite en un électron et un antineutrino. L'important ici est que cette interaction est faible, ce qui signifie en pratique que la transmutation d'un neutron en proton est un événement très rare. Les noyaux riches en neutrons sont donc susceptibles de se transmuter en émettant des antineutrinos et des électrons (ce sont ces derniers qui constituent le rayonnement ß- (bêta moins, moins parce que l'électron possède une charge négative). Ces noyaux sont en bleu sur la carte. C'est par exemple le cas du potassiumpotassium 40 (1 noyau de potassium sur 8000 dans la nature) qui devient du calciumcalcium 40 en émettant un électron dont l'énergie varie de 0.52 MeV (si l'antineutrino n'emporte pas d'énergie) à zéro (si l'antineutrino emporte toute l'énergie) ?
Les noyaux riches en protons disposent, eux, du processus inverse dans lequel un proton se transforme en neutron, en émettant un positronpositron (l'anti-électron) et un neutrinoneutrino. Le proton étant plus léger que le neutron, il faut disposer de plus d'énergie pour compenser cette différence de masse, à laquelle s'ajoutent les 0.511 MeV de la masse du positron. La transition ß+ est donc plus exigeante en énergie. Quand elle est impossible, le noyau dispose encore de la faculté de capturer un des électrons du nuagenuage qui l'entoure. Encore faut-il pour cela que cet électron passe assez près du noyau, ce qui est rare (le noyau a une taille de quelques fermis, alors que le nuage électronique a une taille de plusieurs centaines de milliers de fermis). La capture électronique est donc également un processus très rare. Les noyaux susceptibles de se transmuter soit par transition ß+ soit par capture électronique sont en orange sur la carte. Ces différents modes peuvent d'ailleurs coexister : le potassium 40 se transmute 89 fois sur 100 en calcium 40 par transition ß- et 11 fois sur 100 en argonargon 40 par capture électronique.
Dans certains cas enfin, il arrive que l'expulsion d'un neutron ou d'un proton soit la solution la plus économique. Cela concerne quelques noyaux légers, en mauve et en rouge sur la carte.
Il existe enfin un autre type de transition qui ne change pas l'identité du noyau, la transition gamma. Après une des transitions précédentes, le noyau final n'est pas nécessairement en équilibre, il se trouve même fréquemment dans un état excitéétat excité où l'un des nucléons a plus d'énergie qu'il ne devrait. Il retombe alors vers un niveau plus stable en émettant son excès d'énergie sous la forme d'un photonphoton. Le mécanisme est similaire à celui de l'émission de photons par les atomesatomes, à ceci près que le photon a beaucoup plus d'énergie et donc une longueur d'ondelongueur d'onde beaucoup plus courte que la lumièrelumière visible ou les rayons Xrayons X : ce sont les rayons gammasrayons gammas. Le noyau peut d'ailleurs émettre plusieurs photons gammas en cascade dans ce processus de désexcitation. Par exemple, le cobaltcobalt 60 se transmute par ß- en nickelnickel 60 excité, qui se désexcite immédiatement en émettant en cascade deux photons gamma de 1.17 MeV et 1.33 MeV. Sauf cas très exceptionnels, la transition gamma est beaucoup plus rapide que les transitions alpha ou bêta, et est instantanée à l'échelle humaine.
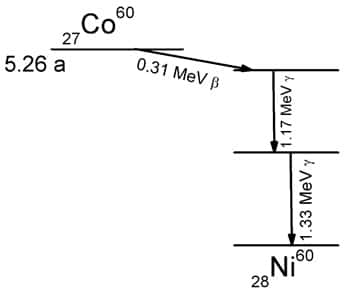
Transmutation radioactive bêta du cobalt 60 en nickel 60, suivie de deux désexcitations gamma du nickel 60 vers son niveau fondamental © Wikipedia
Le noyau résultant d'une transmutation peut fort bien être radioactif lui aussi. Il se constitue ainsi des chaînes radioactives, des suites de noyaux se transmutant en cascade. À un instant donné, le noyau « père » coexiste avec toute la chaîne de ses descendants (équilibre radioactif). Les plus connues sont les chaînes de désintégration alpha des noyaux lourds, par exemple celle qui conduit de l'uranium 238 au plombplomb 206, en passant par le radiumradium 226, le radonradon 222, ou le poloniumpolonium 210.
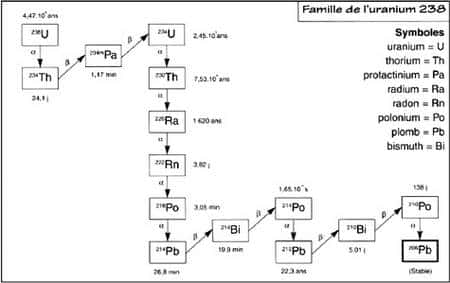
Chaîne radioactive de l’uranium 238 © Société Française de Radioprotection
Chaque désintégration alpha diminue de 2 le nombre de protons et de 2 le nombre de neutrons. Les noyaux successifs deviennent de plus en plus excédentaires en protons, et l'équilibre se rétablit en entrecoupant les transitions alpha par des transitions ß+.
Les différents mécanismes permettant la transmutation de noyaux ont plusieurs points communs. Tout d'abord ils ont leur origine à l'intérieur du noyau et les énergies mises en jeu sont considérablement plus élevées que celles des liaisons chimiquesliaisons chimiques des atomes. Cela explique qu'ils soient totalement insensibles aux combinaisons chimiques dans lesquelles les atomes sont associés : la radioactivitéradioactivité de l'uranium est la même qu'il soit sous forme métallique, sous forme d'oxyde ou sous forme d'hexafluorure. Elle ne dépend pas non plus de la température (tant qu'elle ne dépasse pas quelques centaines de milliers de degrés) ou de la pressionpression. Il ne suffit pas de chauffer du plomb sur un fourneau pour obtenir de l'or.
Ensuite, les processus de transmutation sont peu probables, ce qui signifie qu'un noyau attend très longtemps avant une transmutation. Très longtemps s'entend ici comparé à l'échelle de temps du noyau, 10-21 s. Cela peut être très court (ou très long) à l'échelle humaine !
Mais surtout le processus de transmutation est quantique, qu'il s'agisse de l'effet tunnel pour les fissions spontanées ou les transitions alpha, de l'émission d'un boson W pour les transitions bêta, d'une capture électronique, ou de l'émission d'un photon gamma. L'origine quantique de ces processus en fait un phénomène aléatoire : il est impossible de savoir quand un noyau donné va se transmuter. Par contre il possède une probabilité p bien définie de se transmuter par unité de temps, la même pour tous les noyaux d'un type donné, et indépendante du temps ou de l'environnement chimique ou thermique du noyau. Cela implique que sur N noyaux, Np se transmutent en moyenne chaque seconde. C'est un processus de PoissonPoisson, à chaque seconde le nombre effectif de noyaux muté peut être un peu plus grand ou plus petit que Np avec une dispersion √Np autour de la valeur moyenne.
On définit l'activité d'un échantillon comme le nombre de transmutations par seconde dans cet échantillon. L'unité est le becquerel (1 Bq = une transmutation par seconde). Comme le nombre N(t)p de noyaux transmutés chaque seconde est proportionnel au nombre N(t) de noyaux radioactifs à cet instant, ce nombre diminue exponentiellement avec le temps : N(t)=N(0) exp{-t/τ} avec une échelle de temps de décroissance τ=1/p caractéristique du noyau radioactif. Au bout d'un temps t1/2= τln2, le nombre de noyaux radioactifs est divisé par deux, aussi appelle-t-on cette duréedurée t1/2 la demi-viedemi-vie ou période radioactive. C'est plus souvent t1/2 que τ que l'on trouve dans les tables.
Le tableau suivant donne quelques périodes de noyaux d'usage courant. Remarquons l'énorme éventail de périodes (de la picosecondepicoseconde à plusieurs milliards d'années), et notons que l'éventail est aussi large pour les transitions alpha que pour les transitions bêta.
| Noyau | Période | Mode |
| Uranium 238 | 4.47 milliards d'années | Alpha |
| Potassium 40 | 1.28 milliards d'années | Bêta |
| IodeIode 129 | 15.7 millions d'années | Bêta |
| PlutoniumPlutonium 239 | 24 000 ans | Alpha |
| CarboneCarbone 14 | 5730 ans | Bêta |
| Radium 226 | 1602 ans | Alpha |
| CésiumCésium 137 | 30 ans | Bêta puis gamma |
| StrontiumStrontium 90 | 28 ans | Bêta |
| Cobalt 60 | 5.26 ans | Bêta puis gamma |
| Polonium 210 | 138 jours | Alpha |
| Iode 131 | 8 jours | Bêta |
| Iode 130 | 12 heures | Bêta |
| Iode 132 | 2.3 heures | Bêta |
| Polonium 216 | 158 millisecondes | Alpha |
| Polonium 212 | 0.3 microsecondes | Alpha |
Il y a bien évidemment une corrélation inverse entre période et activité : un gramme d'une substance de nombre de massenombre de masse A et de période t1/2 a une activité de 1.3x1016x(1 an/t1/2)/A becquerels. Cela semble colossal, parce que le becquerel est une unité minuscule. Si la radioactivité d'un gramme de radium est de 37 milliards de becquerels (c'était l'ancienne unité d'activité, la curie), celle d'un gramme d'uranium n'est de 12 000 becquerels. Les objets courants de notre environnement sont toujours un peu radioactifs : 13 Bq pour un litre d'eau de mer, 1000 Bq pour un kgkg de granit, 7000 Bq pour un corps humain (4500 dus au potassium 40, 2500 dus au carbone 14). Ces radioactivités, aussi faibles soient-elles, sont facilement détectables et mesurables.
Si l'on revient à la carte des périodes des noyaux en fonction du nombre de neutrons et de protons, on remarque que la vallée de stabilité est en fait formé de deux régions séparées par une zone d'instabilité intense, entre le bismuthbismuth (Z=83, N=126) et le radium (Z=88, N=138), où les périodes ne dépassent pas quelques secondes. Les théoriciens pensent qu'il devrait exister une troisième région de la vallée pour des masses encore plus hautes, au-delà de Z=114 et N=184, où les périodes pourraient dépasser plusieurs jours. Quelques noyaux de l'élément 114, provisoirement appelé ununquadium (un-un-quatre), ont été synthétisés en 1999 en Russie, à Doubna (qui a donné son nom à l'élément Z=105, le dubniumdubnium), avec une période de quelques secondes. Des éléments plus stables pourraient donc bien exister dans cet « îlot de stabilité ».
Mais justement, comment tous ces noyaux se sont-ils formés ?