Symétrie et invariance

Par constructionconstruction, chaque classe S est un ensemble invariant sous l'action de la transformation TT. Mais les règles qui définissent T ne sont pas forcément connues à priori. 

Effet spriale. © Geralt, Pixabay, DP

Le plus souvent, on constate la présence d'invariances, de régularités qui permettent une classification avant même de savoir précisément s'il y a une symétrie sous-jacente. La relation « appartient au même sous-ensemble que » ou « a la même propriété que » définit immédiatement une relation d'équivalence et la propriété en question est, par définition, un invariant dans chaque classe. En taxinomietaxinomie, la division classique des organismes vivants en ordres, familles, genres, espècesespèces, etc. est effectivement fondée sur un ensemble de caractères communs, les invariants, qui permettent du même coup une nomenclature.

Les invariants

Que la présence d'un invariant, après avoir été découverte et confirmée, soit intégrée ensuite au niveau théorique dans une définition est un changement de statut très fréquent qui participe à la progression scientifique. La définition de l'oxygène donnée ci-après n'était assurément pas celle d'Antoine LavoisierAntoine Lavoisier. L'invariance de la vitesse de la lumière dans le vide était d'abord un fait expérimental et une clef de voûte théorique de la relativité einsteinienne avant de fournir une définition du mètre. Le basculement inverse se rencontre aussi : on peut partir de la présence d'une corrélation fréquente entre certains caractères observés chez les oiseaux (couleur, forme du bec, taille, régime alimentaire, comportement social, habitat, etc.) pour forger la définition « un cygne est un oiseauoiseau blanc aux pattes palmées, au long cou, etc. » Cependant, les ornithologuesornithologues préfèrent une définition qui ne repose pas sur la couleur, et l'énoncé « tous les cygnes sont blancs » devient alors une proposition susceptible d'être mise à l'épreuve de l'expérience et qui, en l'occurrence, se trouve être fausse.

En chimie, la classification périodique des éléments permet d'organiser l'ensemble des atomes. Par exemple, on appelle oxygène la classe des atomes électriquement neutres qui possèdent 8 électronsélectrons. D'ailleurs, électron désigne toute particule de la classe des fermionsfermions de spinspin 1/2, de charge e = -1,6 x 10^-19 C, de massemasse m_e = 0,511 MeV/c², etc. Le fait que les particules quantiques ne soient caractérisées de façon unique que par une petite poignée d'invariants (spin, charge, masse, couleur, saveur, pour ne citer que les invariants élémentaires) [voir la note en bas de page, NDLRNDLR] non seulement a permis de mettre à profit les transformations où les particules sont échangées les unes avec les autres (permutations), mais encore a conduit à l'idée que les particules apparaissaient comme des excitations indiscernables de champs quantiques, susceptibles d'être créées ou détruites.

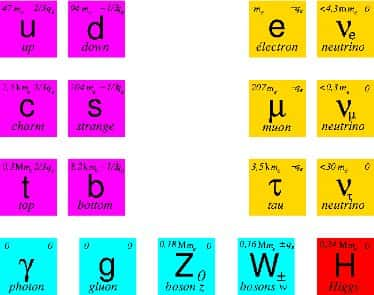
Les particules considérées à l'heure actuelle comme élémentaires dans le modèle standard s'organisent en fonction de groupes de symétries. © Amaury Mouchet, Dunod

La question de savoir si derrière chaque invariant se profile une symétrie est particulièrement délicate. Certes, on peut toujours classer tout et n'importe quoi. À partir de deux objets à priori non équivalents, on peut toujours définir de façon ad hoc une symétrie qui les relie et les rend équivalents à posteriori.

Cette opération peut vite s'avérer artificielle et stérile ; elle ne devient pertinente que si l'on retrouve cette symétrie dans d'autres situations, entre d'autres paires d'objets. Considérons par exemple un cercle et une ellipse non circulaire dans le plan. Si l'on compose de façon appropriée une translationtranslation et deux dilatationsdilatations, on peut facilement expliciter une symétrie qui transforme le cercle en l'ellipse. Ces transformations sont omniprésentes, en géométrie comme ailleurs, alors que les transformations qui métamorphosent une citrouillecitrouille en un carrosse, que l'on parle des corps tridimensionnels ou de la morphose (morphingmorphing) de deux images, ont une portée nettement moins universelle. La raison en est que la transformation réversibleréversible dans ce dernier cas contient autant d'information que les objets à transformer, alors que les transformations pertinentes doivent permettre de réduire l'information et, d'une certaine façon, acquérir une certaine autonomieautonomie vis-à-vis des objets sur lesquelles ils agissent. Ce dernier exemple, lorsqu'il est transposé aux objets quantiques, devient moins surréaliste (quoique... la question du réalismeréalisme en physique quantique est un vaste programme). La symétrie qui permet de transformer formellement un protonproton en un neutronneutron (symétrie d'isospin) a joué un rôle important dans la classification des particules subatomiques et la compréhension de leurs réactions avant l'avènement de la théorie plus satisfaisante des quarksquarks. L'introduction d'une symétrie qui échange fermions et bosonsbosons (supersymétrie, SuSy pour les intimes) permet de résoudre un certain nombre de problèmes théoriques (tout en en soulevant d'autres, évidemment), mais n'a pas encore pu être mise en évidence expérimentalement.

L'invariance en physique

En physiquephysique, surtout à partir du XX^e siècle, le rôle des symétries a pris une ampleur considérable. La généralisation de la notion de symétrie bien au-delà des transformations spatiotemporelles usuelles (globales), par exemple en prenant en ligne de compte des transformations de jauge (globales ou locales) ou les permutations de particules identiques, leur a permis d'acquérir un pouvoir d'une féconditéfécondité étonnante : les contraintes qu'elles imposent sont si restrictives qu'elles permettent non seulement de discriminer radicalement les modèles théoriques, mais encore de fournir d'élégants principes unificateurs et fondateurs dont l'efficacité relève du prodige. Par exemple, l'invariance par changement de référentielréférentiel accéléré constitue une pierre angulaire de la relativité généralerelativité générale dès sa conception. Les symétries de jauge, induites en partie par les règles de sélection observées dans les accélérateurs de particules, ont joué un rôle essentiel dans la détermination des ingrédients du modèle standard.

Par ailleurs, dans les systèmes complexes (notamment en physique statistique pour décrire les transitions de phasestransitions de phases ou les spectresspectres d'hamiltoniens à grand nombre de degrés de liberté), des arguments fondés presque exclusivement sur l'existence de certaines symétries conduisent à des résultats très précis, qualifiés d'universels, c'est-à-dire où les détails microscopiques importent beaucoup moins que les symétries elles-mêmes. On retrouve ici de façon plus précise l'idée de la projection. La réduction de l'information, que mesure l'entropieentropie, est non seulement inévitable, mais par-dessus tout pertinente.

De façon générale, la dynamique (classique ou quantique) d'un système hamiltonienhamiltonien dépend avant tout du nombre de constantes du mouvementmouvement indépendantes, lui-même intimement lié par le théorèmethéorème de Noether aux symétries de l'action. Par exemple, en physique classique il suffit que ce nombre devienne strictement inférieur au nombre de degrés de liberté pour faire basculer la dynamique (pour certaines, sinon toutes les conditions initiales) d'un régime régulier à un régime irrégulier (chaotique). En physique quantiquephysique quantique, les corrélations spectrales des énergiesénergies dépendent essentiellement des symétries de l'hamiltonien : avoir autant d'opérateurs indépendants qui commutent entre eux que de degrés de liberté autorise les dégénérescences spectrales, alors que dans le cas contraire, les niveaux d'énergie ont tendance à se repousser plus nettement les unes des autres.

Note : un théorème établi en 1918 par la mathématicienne Emmy NoetherEmmy Noether dresse le pont entre invariance par groupe (continu) de symétrie et l'existence d'invariants, plus généralement de lois de conservation comme celle de l'énergie ou de la quantité de mouvementquantité de mouvement.