au sommaire
Les transformations géométriques comme la symétrie miroir ou une rotation s'appuient exclusivement sur l'espace sans jamais faire intervenir le facteur temps. Les physiciensphysiciens enrichissent cette panoplie de transformations en lui ajoutant des transformations dépendantes du temps (transformations dynamiques).

Coucher de soleil. © Quangle, Pixabay, DP
Par exemple, on peut déplacer sans le tourner un objet au cours du temps avec une vitesse constante (translation uniforme)) ou non (translation accélérée ou décélérée). L'angle d'une rotation peut aussi se modifier avec le temps. En fait, toute évolution d'un système d'un instant à l'autre est elle-même considérée comme une transformation résultant de l'enchaînement (la composition) d'évolutions intermédiaires.
Au demeurant, si la « flèche du temps » nous apparaît toujours avoir la même « direction » parce que nous sommes gouvernés et entourés de phénomènes irréversibles, les physiciens n'hésitent pas à simuler l'inversion du sens du temps dans leurs modèles (à passer le film des événements à l'envers) pour mieux comprendre le déroulement de certains processus ou reconstituer une histoire. Ce renversement du sens du temps qui échange futur et passé, causes et effets, est l'équivalent temporel de la symétrie miroir qui échange haut et bas ou gauche et droite.
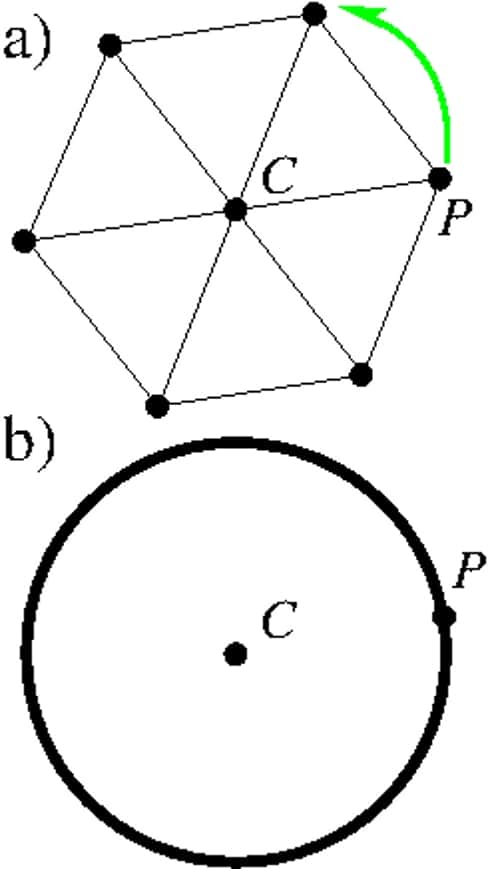
La répétition de la rotation d'un sixième de tour du point P autour du centre O transforme P en tous les sommets d'un hexagone (en a). Si l'on considère l'ensemble continu des rotations d'un angle quelconque, on obtient un cercle de centre O (en b). © Amaury Mouchet, Dunod
Les transformations dans l'histoire, de Galilée à la physique quantique
Quand Galilée propose de comparer des expériences effectuées dans la cabine d'un navire en mouvement (par rapport au rivage) avec celles effectuées à l'arrêt, il marque l'entrée en scène de la physique au sens moderne du terme, sa « Renaissance », pour ainsi dire. La transformation envisagée concerne l'expérimentateur et ses expériences, puisqu'on les embarque (transforme) tous ensemble à bord du navire.
Les translations rectilignes uniformes se retrouveront au cœur de la relativité restreinte, mais sous une autre forme (groupe de Poincaré-Lorentz plutôt que groupe de GaliléeGalilée). Le principe d'équivalence en relativité généralerelativité générale exprime lui aussi une invariance par un groupe de transformations, mais cette fois étendu (généralisé) aux changements entre référentielsréférentiels accélérés.
L'avènement de la physique quantique au début du XXe siècle s'est accompagné de deux autres types de transformations, qui se sont avérées singulièrement pertinentes pour décrire le monde microscopique : les transformations d'échange et les transformations de jauge.