Les grands travaux géodésiques

Quels sont les grands travaux géodésiques ? Quand la cartographie est-elle née ? Partez sur les traces d'Al-KashiAl-Kashi, de Christian HuygensChristian Huygens, René DescartesRené Descartes ou encore Isaac NewtonIsaac Newton. 

Quels sont les grands travaux géodésiques ? © Lance87, DP

Naissance de la cartographie

En 2400 av. J.-C., les Mésopotamiens établirent les premières cartes sur des tables d'argileargile. En ces temps reculés, la Terre était imaginée au centre de l'univers et la mer Méditerranéemer Méditerranée au centre du monde. Les Romains dressèrent à partir du III^e siècle des cartes routières détaillées de leurs territoires. Les guerres portées par les Césars de Rome dans le but d'agrandir l'Empire nécessitèrent des supports graphiques représentant le relief et l'environnement. La cartographie était née.

Mais, pour établir ces cartes, il faut faire appel à des relevés de terrain. La topographie représente ces techniques de mesures pratiques qui vont permettre l'établissement de plans avec indication des reliefs. La cartographie et la topographie sont dès lors définitivement indissociables.

Le désir d'agrandir la représentation des cartes à des étendues toujours plus grandes nécessita des études plus globales, au niveau de notre planète. La géodésiegéodésie est la science qui étudie les formes, les dimensions et le champ de gravité de la Terre (étymologiquement, du grec gê, « terre », et daiein, « diviser »). On étudie ces caractéristiques par points localisés via la topographie et la cartographie.

L'alliance de la géodésie, de la topographie et de la cartographie permet sur le globe un positionnement précis en attribuant à une carte des jeux de coordonnées dans un ou plusieurs systèmes de référence mondiaux ou plus localisés.

Acteurs principaux de la géodésie durant l'Antiquité et au Moyen Âge

Depuis ÉratosthèneÉratosthène, les diverses techniques de calculs géodésiques se sont améliorées très rapidement. Vers l'an 1000, Al-Biruni mit en pratique ces techniques en y adaptant de subtils procédés trigonométriques. D'origine perse (Iran de nos jours), philosophe, diplomate, astronomeastronome et mathématicienmathématicien, il entreprit de nombreux voyages, en Inde notamment, où il étudia puis enseigna les sciences transmises par les Grecs.

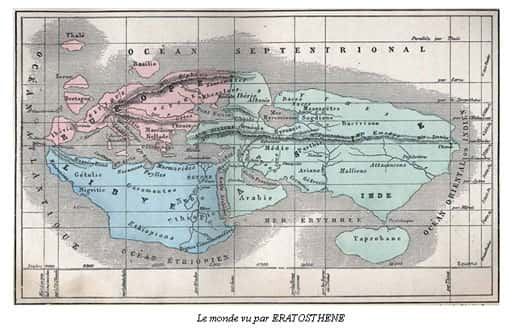
Le monde vu par Ératosthène. © DR

Al-Biruni calcula avec précision les densités et poids usuels en appliquant les principes d'ArchimèdeArchimède. Il écrivit aussi un traité sur la règle de trois, qui est un traité sur le calcul des proportions. Sa plus grande contribution aux mathématiques fut sans nul doute en trigonométrie (11 livres) ; reprenant et corrigeant les résultats de PtoléméePtolémée, il établit des tables très précises : calcul des demi-cordes (futur sinus) par pas de 15' d'angle, et des tangentes par pas de 30' avec quatre sexagésimales de précision. Il appliquera tout cela à des méthodes de triangulationtriangulation géodésique, comme avec le rayon terrestre en calculant au préalable un arc de méridien de 1°.

Archimède. © DP

On doit aussi beaucoup à Al-Kashi (env. 1350 à env. 1439). Iranien d'origine, il fut astronome sur le territoire de l'actuel Ouzbékistan et l'un des plus grands mathématiciens du début du XV^e siècle. Il rendit courant l'usage des nombres sexagésimaux (qu'utilisaient déjà les Babyloniens). Il définit par la suite le dixième de l'unité, puis le centième, etc. Ce fut grâce à la méthode des périmètres qu'il calcula dans le Traité sur le cercle (1424) le rapport de la circonférence d'un cercle à son rayon, c'est-à-dire 2π, en base 60 ainsi qu'une excellente approximation (par conversion qu'il exprime) alors jamais atteinte avec 16 décimales : 2π = 6,2831853071795865. Mais ce n'était encore qu'un rapport, comme l'avait déjà étudié Archimède, et il n'a pas le statut d'un nombre.

Ce ne fut qu'en 1647 que le mathématicien William Oughtred (1574 à 1660) utilisa la 16^e lettre de l'alphabet grec pour lui donner ce statut. Toutefois, il fallut attendre le mathématicien Leonhard EulerLeonhard Euler (1707 à 1783) et le succès de son ouvrage Introduction à l'analyse infinitésimale (1748) pour voir la lettre π s'imposer comme notation du nombre PiPi.

Mais revenons à Al-Kashi : par la suite, dans son traité La Clé de l'arithmétique (1427), il décrivit aussi l'utilisation des racines n-ièmes d'un nombre grâce à des formules de calcul approché. On doit bien évidemment à Al-Kashi la généralisation du théorème de Pythagore en l'exprimant sous la forme a^² = b^² + c ^²- 2bc.cosÂ. Ces calculs sont des bases inévitables utilisées par la suite en mathématiques pour la géodésie.

Les pères de la géodésie moderne

Cela étant, la paternité de la géodésie comme science à part entière est souvent attribuée à l'astronome hollandais Snellius, né en 1580 à Leyde, où il enseigna les mathématiques. Selon Christian Huygens, Snellius découvrit le premier (en 1621) les lois de la réfractionréfraction, qui sont une branche fondamentale de l'observation astronomique. Ces lois, dites en France « lois de Descartes », sont souvent appelées « lois de Snell-Descartes » en dehors de nos frontières.

Portrait de Descartes. © DP

René Descartes, né en 1596, était avant tout philosophe. Il se forma lui-même aux sciences et se distingua particulièrement en métaphysique. Dans ce courant de pensée, il fit ressortir une des plus grandes vérités : « Cogito ergo sum », la fameuse phrase « je pense donc je suis », dont il se servit pour établir l'existence de l'âme, à laquelle il donne pour essence la pensée. Il fit aussi ressortir la distinction entre l'esprit et la matièrematière. Descartes était extrêmement compétent en mathématiques, physiquephysique et astronomie aussi. Grâce à lui, l'algèbre fit un grand pas, notamment avec son nouveau mode de notation, celui des exposants, qu'il appliqua à la géométrie des courbes. Il mourut en 1650.

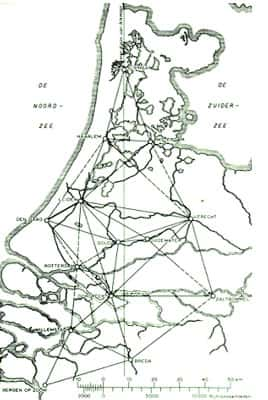
Les triangles de Snellius. © DP

Il semblerait que l'on doive à Snellius l'écriture actuelle des nombres décimaux, en France tout au moins, qui sépare par une virgule d'une part les parties entières et d'autre part les parties décimales.

La célèbre loi de la réfraction avait été conjecturée vers l'an 1000 par Ibn al-Haytham, un brillant mathématicien, physicienphysicien, astronome et philosophe arabe qui étudia avec beaucoup d'attention l'anatomieanatomie de l'œilœil pour des recherches en optique. Ses œuvres firent l'apogéeapogée de la physique arabe. Huygens donna une preuve simple de la loi de la réfraction en posant comme principe la nature ondulatoire de la lumièrelumière. On doit à Snellius les premiers calculs trigonométriques visant à calculer l'arc du méridien allant de Alkmaar à Berg-op-Zoom en passant par Leyde (en 1617, cela représentait la vraie valeur du pourtour de la Terre).

Christian Huygens. © DP

Entre-temps, des raisons théoriques suggérèrent que la forme de la Terre ne devait pas être exactement celle d'une sphère. Christian Huygens (1629-1695) né à La Haye, grand savant touchant à l'astronomie et l'horlogerie mais aussi géomètregéomètre et diplômé de droit, ainsi que Isaac Newton partirent de l'hypothèse que notre globe aurait été primitivement à l'état fluide.

Ils démontrèrent en effet que la surface de la Terre devait être plutôt un ellipsoïde de révolution autour de la ligne des pôles, c'est-à-dire que le petit axepetit axe est le même que l'axe des pôles. Ce qui était contraire à l'époque à la manière de penser de la famille Cassini, plus particulièrement de Jacques Cassini, fils de Jean-Dominique CassiniJean-Dominique Cassini, qui était très cartésien et totalement contre l'idée de l'aplatissementaplatissement des pôles. Les preuves apportées par Newton et Huygens le forcèrent à abandonner cette farouche idée.

Isaac Newton. © DP

Il laissa à son fils Cassini de Thury le soin de réaliser l'établissement de la carte de France et, petit à petit, il abandonna les sciences pour se consacrer à d'importantes tâches administratives au sein de l'État. Huygens démontra que le mouvementmouvement de la Terre crée la force centrifugeforce centrifuge et expliqua la diminution de la pesanteur de l'équateuréquateur. C'est lui qui affirma le premier que les directions des vecteurs de champ ne sont pas dirigées vers le centre de notre globe. Toutes les mesures d'observation qui suivirent contribuèrent à confirmer l'aplatissement des pôles. Cette vue de la planète est aujourd'hui la base des calculs géodésiques pour les projections planes, car, sans le savoir, il exprima le fait que la Terre se comporte finalement comme un fluide et que l'ellipsoïde n'est rien qu'un modèle mathématique de la Terre, la véritable représentation n'étant autre que le géoïdegéoïde...

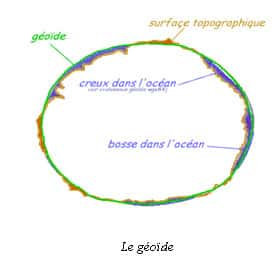
Le géoïde.  © DR

Le géoïde

Ce n'est qu'au XX^e siècle que fut vraiment utilisée la notion de géoïde. Il s'agit d'une surface en équilibre, la Terre se comportant comme un fluide. Or, la surface de niveau d'un fluide en équilibre est en tout point normale aux forces de pesanteur.

Le géoïde est donc une surface équipotentielle du champ de pesanteur coïncidant au mieux avec le niveau moyen des océans. Il est défini à une altitude près. Pour la France, il est calé sur un niveau zéro scellé dans le port de Marseille. Le géoïde est une surface difforme, à laquelle on ne saurait appliquer des relations mathématiques. L'ellipsoïde est là pour représenter les formulations mathématiques, pour exprimer des coordonnées géographiques afin d'effectuer des calculs qui permettront l'établissement de cartes et de plans via des projections planes 2D des points 3D de l'ellipsoïde. Il y a donc une relation entre ellipsoïde et géoïde. Des mesures de champ de gravité réalisées par des satellites géodésiques ont montré des irrégularités plus ou moins corrélées avec la topographie, n'excédant pas 100 m par rapport à un ellipsoïde de révolution autour de l'axe terrestre.

À notre époque, tous les ellipsoïdes de référence existants ont des caractéristiques communes : leur centre est proche de la Terre, leur petit axe est proche de l'axe des pôles et leur aplatissement et leur taille sont proches de ceux de la Terre. Néanmoins, leurs dimensions plus générales peuvent différer. On distingue une bonne dizaine d'ellipsoïdes sur la planète. En France, on en utilise principalement quatre :

• L'ellipsoïde de Clarke 1880 est associé au réseau géodésique français NTF et à la projection conique plane de Lambert. Cet ellipsoïde a été utilisé pour la confection de la carte de France au 1/25.000^e que nous utilisons tous. Alexander RossRoss Clarke a calculé en 1858 le rayon équatorial, le rayon polaire, et, par conséquent, la valeur de l'aplatissement de la planète. Jean-Henri Lambert (1728 à 1777), né à Mulhouse, mathématicien, physicien, astronome, fit de nombreux travaux sur π.

• L'ellipsoïde de Hayford 1909 est utilisé avec le système européen ED50 et une projection plane UTM. John Fillmore Hayford, ingénieur, reprend quelques mesures géodésiques et démontre que l'aplatissement des pôles calculé par Clarke était un peu surestimé. Sa nouvelle valeur est encore employée de nos jours.

• L'ellipsoïde IAG-GRS 80 est utilisé avec le nouveau réseau géodésique français, extrêmement précis (la précision relative mesurable entre 2 points du réseau est de 1 mm/km sur les points de détail, 0,4 mm/km sur les points de base et 0,1 mm/km sur les points de référence).

• L'ellipsoïde WGS 84 est le système mondial mis au point par la Défense des États-Unis pour des applicationsapplications militaires par GPSGPS. Il n'a qu'une précision métrique et nécessite des transformations vers d'autres ellipsoïdes pour des applications plus précises.

Actuellement, les méthodes géodésiques modernes utilisent des outils comme les systèmes de positionnementsystèmes de positionnement par satellite, GPS. Ce sont des méthodes dites « modernes ». Cassini de Thury (petit-fils de l'astronome Jean-Dominique Cassini) utilisa les méthodes dites « classiques » lorsqu'il effectua les travaux du premier réseau géodésique français afin de réaliser la tâche que lui avait confiée son père : cartographier la France. Ces travaux furent achevés en 1784. La France était alors cartographiée sur 180 feuilles.

Cartographier la Terre, un travail de fourmi. © DR

Triangulation et trigonométrie

Le principe de détermination était le suivant : on démarrait les mesures en partant d'un point connu dont les coordonnées étaient définies par des visées astronomiques (en France, la croix du Panthéon). De ce point partaient des chaînes de triangles adjacents de 1^er ordre, de 30 à 50 km de côté, dont les sommets étaient matérialisés (et le sont encore de nos jours) par des bornes spécifiques. La mise à l'échellemise à l'échelle était réalisée par des mesures de bases linéaires, dans des zones plates et dégagées. Les réorientations étaient obtenues par d'autres visées astronomiques. Ces figures étaient ensuite densifiées en sous-réseaux de 2^e, 3^e ordre... en triangles de plus en plus petits en incluant le maximum de points hauts en altitude du territoire (clochers, sommets naturels...) déterminés par des visées d'intersection.

Si la Terre était plate, il serait plus aisé de mesurer les distances. Or, un chemin rectiligne allant d'un lieu A à un lieu B de la Terre est en fait approximativement un arc de cercle. L'idée de la triangulation est donc de pallier ce problème naturel qu'est l'arc terrestre par des segments de droites et de substituer fondamentalement la seule mesure des angles aux mesures des distances.

L'usage de la trigonométrie plane apporte bien sûr quelques erreurs car c'est en fait la trigonométrie sphérique qui devrait plutôt s'appliquer. Mais, pour des distances réduites (quelques kilomètres), fruit de la triangulation, ces erreurs sont faibles. De plus, Legendre apporta de subtiles formules de corrections qui rendirent la méthode de la triangulation extrêmement précise.

Cercle répétiteur utilisé par Delambre et Méchain. © DR

Les nouveaux outils de l'époque, notamment ceux de Jesse Ramsden, couplés à ces méthodes, permirent à l'abbé Jean Picard (1620-1682), astronome français, de mesurer l'arc de méridien avec une grande précision. Jean Picard calcula une distance de 57.060 toises pour 1° d'arc. Une autre excellente application de la triangulation fut une très bonne approximation de la distance Terre-LuneLune, qui a été établie en 1751 par les astronomes français Joseph Jérôme Lefrançois de Lalande (1732-1807) et l'abbé Nicolas-Louis de Lacaille (1713-1762) en observant la Lune au même instant à Berlin (Allemagne) et Le Cap (Afrique du Sud). Les mesures de ces deux savants confirmèrent les résultats de Jean Picard.

Grâce aux progrès des calculs trigonométriques utilisés dans ces mesures par Jean-Baptiste Joseph Delambre (1749-1822), Gaspard Monge (1746 à 1818) et Adrien-Marie LegendreAdrien-Marie Legendre (1752 à 1833) en particulier, la géodésie devint une branche importante des mathématiques. Delambre suivit au Collège de France les cours du célèbre Lalande, qui l'initia à l'astronomie. Membre de l'Académie des sciences en 1795, il cofonda le bureau des longitudeslongitudes qui avait pour but de maîtriser mieux que les Anglais les techniques de détermination des longitudes afin de mieux naviguer en mer, ainsi que le perfectionnement des tables astronomiques. Ce bureau eut d'autres missions par la suite. Quant à Legendre, il tient une place importante dans l'histoire des mathématiques. Professeur de l'École militaire, à Paris, puis de l'École normale, il étudia notamment l'irrationalité de π² et les intégrales elliptiques.

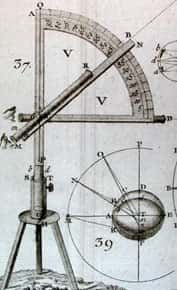
Astronomie et géodésie vont de pair. © DR

Lors de la Révolution, époque à laquelle l'on voulut définir le système métrique, Delambre et Pierre François André Méchain (1744-1804) furent chargés par l'Assemblée constituante (en 1791) de calculer la longueur de l'arc de méridien Dunkerque-Barcelone, afin de définir le « mètre ». Méchain, grand astronome, découvrit douze comètescomètes ainsi que le caractère planétaire d'un astreastre découvert par l'astronome Herschel en 1781 et qu'il nomma un an plus tard UranusUranus. C'est en entrant à l'Académie des sciences en 1782 qu'on lui confia cette mission géodésique. Le « mètre » fut déterminé comme étant le dix-millionième du quart du méridien terrestre. Cela prit sept ans.

Ces mesures étaient encore entachées de petites erreurs : déviations locales des verticales, erreurs instrumentales, réfraction imprécise des étoilesétoiles basses. Pourtant, Méchain n'avait commis aucune erreur provenant de sa personne et c'est Perrier, un géographe né en 1833 dans le Gard, qui reprit les travaux de triangulation entre Dunkerque et Barcelone. Il employa des instruments plus aboutis et plus perfectionnés. Il remplaça la méthode de répétition de mesure des angles par celle de la réitération, fit plus de vérifications et supprima définitivement les dernières sources d'erreur sur la mesure des angles en se servant des signaux provenant de l'héliotrope de Gauss, un peu modifié. En 1879, ces mesures étaient terminées entre Melun et Perpignan ; cette dernière possède encore de nos jours d'exceptionnelles bornes géodésiques datant de cette époque.