au sommaire
Alberti pose les bases du calcul de distances par triangulation. La géodésie permet de connaître la distance d'un point par rapport à deux autres connus. © Hulsius, Domaine public, Wikimédia Commons
La géodésie est une science ayant pour but de déterminer la forme et les dimensions de la Terre. C'est une partie des mathématiques qui traite des opérations nécessaires pour lever la carte d'un pays, mesurer un arc de méridienméridien, opérations gravimétriques et spatiales...
- Inventée en 1445 par Leon Battista AlbertiLeon Battista Alberti
Principe de la géodésie
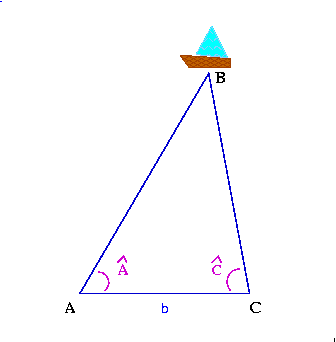
Les opérations géodésiques sont fondées à l'origine sur la triangulationtriangulation qui consiste pour déterminer la distance de deux points donnés à la surface de la terre, à rattacher ces deux points à une base une fois mesurée, à l'aide d'une suite de triangles dont on mesure les angles et que l'on résout ensuite de proche en proche.
Inventeur de la triangulation, architectearchitecte, mathématicienmathématicien et peintre de la Renaissance, Leon Battista Alberti est l'un des premiers à se pencher sur une méthode de calcul des distances éloignées. Il s'agit alors de connaître l'écart entre deux points en se basant sur le théorème de Thalèsthéorème de Thalès. Selon Alberti, il suffit de planter une flèche dans la terre à une certaine distance (calculable) d'une tour, puis de reculer jusqu'à ce que la pointe de la flèche soit dans la même ligne de vue que le haut de la tour. Le théorème de Thalès s'énonce ainsi : soit ABC un triangle, E et F deux points sur les côtés respectifs [AB] et [AC]. Si les droites (EF) et (BC) sont parallèles, alors AE/AB=AF/AC=EF/BC. Selon ce principe, pour une tour de 100 pieds de hauteur et comportant une porteporte de 10 pieds, la longueur BA est dix fois plus importante que la longueur CDCD. C'est le début de la triangulation. Il écrit également un essai sur la perspective, ce qui permettra de mieux analyser les distances par rapport à deux points géographiques. Ce principe sera par la suite développé sur des éléments mouvants, un navire en pleine mer par exemple.
Utilisation de la géodésie
Cependant, la triangulation possède un défaut lié à la forme même de la Terre : basée sur des distances planes, elle ne permet pas de prendre en compte la courbe formée par la forme sphérique de notre planète. Le mathématicien Legendre apporta des corrections aux calculs de base de la triangulation afin de la rendre plus précise. Aujourd'hui, le développement des radars et des satellites permet d'analyser les distances de manière bien moins approximative, mais la triangulation reste la base de tout calcul sommaire de distances.