"Beaucoup de mathématiciens considèrent leur discipline comme un art. Ils travaillent à partir de leurs méthodes spécifiques, mais aussi sur des théories esthétiques s'appliquant à la création artistique. D'un autre côté, un certain nombre d'artistes sont attirés et/ou stimulés par les mathématiques et utilisent des idées développées par les scientifiques." Ce point de vue est celui de Michele Emmer, mathématicien et cinéaste. Zoom sur les relations entre l'art et les maths, l'image et la visualisation, l'esthétique et la pédagogie.

au sommaire

    <br />Le ruban de Moebius (1790-1868) constitue l'un des paradoxes géométriques les plus célèbres et les plus immédiatement compréhensibles. Il suffit de coller les deux extrémités d'un ruban en faisant au préalable subir à l'une d'elles une (ou plusieurs) torsions de 180° sur elle-même. On obtient ainsi une surface "non orientable". Si on la parcourt, on passe sans transition d'une face à l'autre du ruban.<br />&copy; Konrad Polthier, T-U Berlin

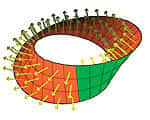
    Le ruban de Moebius (1790-1868) constitue l'un des paradoxes géométriques les plus célèbres et les plus immédiatement compréhensibles. Il suffit de coller les deux extrémités d'un ruban en faisant au préalable subir à l'une d'elles une (ou plusieurs) torsions de 180° sur elle-même. On obtient ainsi une surface "non orientable". Si on la parcourt, on passe sans transition d'une face à l'autre du ruban.
    © Konrad Polthier, T-U Berlin

    Le sens du beau en mathématique doit, pour le moins, remonter à Pythagore. Il n'y a pas de place durable pour des mathématiques moches. L'élégance d'une démonstration, ou la beauté d'une formule peut être, en soi, une direction vers la vérité", estime Osmo Pekonen, mathématicienmathématicien finlandais de l'Université de Jyväskylä, écrivain de surcroît. Quand Pekonen parle de sa discipline, il s'emballe, et son enthousiasme est contagieuxcontagieux. "En physique mathématique, il existe aujourd'hui des théories prédictives hallucinantes, telle celle des supercordes et sa forme la plus récente dite M-Théorie . Elles permettent de rêver à l'existence dans l'Univers de dimensions supérieures, allant au-delà de notre perception usuelle de l'espace-temps, au sein desquelles s'unifierait le jeu des interactions fondamentales - gravitation, électromagnétisme, interactions nucléaires - de la physique contemporaine. Cela semble une fiction et reste expérimentalement invérifiable. Cependant, les théoriciens veulent y croire parce que la beauté des équationséquations les séduit comme le chantchant des sirènes". Henri PoincaréHenri Poincaré ne l'aurait pas démenti, lui pour qui "C'est un vrai sentiment esthétique que tous les vrais mathématiciens connaissent. Et c'est là de la sensibilité".

    Art ou pas, la mathématique nous plonge dans le monde de l'équilibre et de l'harmonie - ses liens avec la musique sont étudiés depuis longtemps - mais aussi de la forme. Ne parle-t-on pas d'objets mathématiques - et d'objets d'art ?

    1 - Plasticité :

    Rendues visibles, presque palpables, les équations perdent de leur opacité. Felix Klein fut l'un des premiers à le comprendre et, dès le XIXe siècle, fit réaliser, en plâtreplâtre, une collection de modèles des fonctions complexes, aujourd'hui rassemblés à l'université de Göttingen. Actuellement, le campus de l'université de Bangor est ponctué de Sculptures symboliques de James Robinson, inspirées notamment des fameux anneaux de Borromée - une idée du mathématicien Ronnie Brown, fondateur du CPM (Centre for the Popularisation of Mathematics) de ladite université. Pour le professeur Brown, "le problème majeur de l'enseignement est de convertir la réalité mathématique en objets mathématiques". Son exposition sur la théorie des nœudsnœuds, appuyée sur une présentation exhaustive et séduisante de ceux-ci, a d'ailleurs connu un franc succès.

    Mais parfois, inversement, l'impulsion vient des artistes. Max Bill, plasticien membre du Bauhaus, a ainsi passé des années à s'interroger sur ces abstractions - et à leur sculpter, à sa manière, une autre vie (voir encadré Sous l'œilœil d'Emmer ). "Est-il besoin de dire que, pour moi, une approche mathématique de l'art ne s'identifie nullement à quelque ingénieux système de calcul reposant sur des formules toutes prêtes ?", écrivait-il en 1949. En ce qui concerne la composition cependant, ajoutait-il, on peut affirmer que toutes les écoles artistiques, jusqu'ici, ont eu des fondations plus ou moins mathématiques.

    2 - Visibilité :

    <br />Illustration d'une autre forme topologique baptisée la Bouteille de Klein , conceptualisée par ce mathématicien en 1882. Cette surface, sans intérieur ni extérieur, et ne possédant aucun bord, tire son nom du fait qu'elle peut être assimilée à une bouteille dont on allongerait puis tordrait le goulot jusqu'à le faire pénétrer dans son corps pour le relier à son fond.<br />&copy; Konrad Polthier, T-U Berlin

    Illustration d'une autre forme topologique baptisée la Bouteille de Klein , conceptualisée par ce mathématicien en 1882. Cette surface, sans intérieur ni extérieur, et ne possédant aucun bord, tire son nom du fait qu'elle peut être assimilée à une bouteille dont on allongerait puis tordrait le goulot jusqu'à le faire pénétrer dans son corps pour le relier à son fond.
    © Konrad Polthier, T-U Berlin

    Plus récemment, les mathématiques ont trouvé un nouveau média via l'informatique. L'infographie a permis de visualiser des problèmes connus, de comprendre comment en résoudre d'autres, et parfois d'aider de nouvelles recherches - en particulier en géométrie. "Le point de départ a été la découverte (ou l'invention) de nouveaux algorithmes qui ont généré des formes inédites. Dans une sorte de nouvelle Renaissance, les mathématiciens et les artistes se sont lancés dans une coopération inédite, utilisant ce que l'on appelle la visualisation mathématique, explique Michele Emmer, professeur à l'Université de Rome. L'importance de ces images virtuelles et la possibilité de les animer ne cesse de croître en mathématique. Aussi, il semble naturel que tous ces nouveaux aspects visuels intéressent également les artistes. On sait que dans certains cas, par exemple à la Renaissance, il n'était pas facile de distinguer un artiste d'un mathématicien... "Ce n'est pas sans raison que le Journal of the International Society for the Arts, Sciences and Technology, dont Emmer est (et Max Bill fut) membre de l'équipe éditoriale, édité par le MIT, s'intitule Leonardo .

    En Allemagne, Konrad Polthier, de la Technische Universität de Berlin, est un adepte passionné de la visualisation mathématique. Il s'est rapidement aperçu que ses recherches sur les formes et les surfaces, impliquant trois dimensions, et parfois plus, étaient trop complexes pour être "représentées" au moyen d'outils "ordinaires". Polthier a donc créé son propre logiciellogiciel, JavaJava View, petit programme adaptable sur tout PCPC possédant un browserbrowser InternetInternet, libre de droits pour des usages non commerciaux. Java permet les calculs les plus divers et leur visualisation sur écran. L'objet virtuel peut être "manipulé" (tordu, allongé, présenté sous d'autres faces...) par un simple cliquement de souris. "Ce logiciel est destiné à enrichir les publications scientifiques grâce à la visualisation. J'aimerais que de nombreux chercheurs l'utilisent, remarque son auteur. Par ailleurs, nous savons que les technologies multimédias gagneront de plus en plus d'importance dans le monde de l'édition. Cela peut paraître un gadget dans certains cas mais, lorsqu'il s'agit de discuter de problèmes mathématiques multidimensionnels ou de décrire des processus complexes en science et en technologie, la visualisation deviendra un élément indispensable."

    Ces formes inédites sont souvent étonnantes et ces images peuvent être fascinantes. "Certaines de ces structures sont si harmonieuses qu'il est presque impossible de ne pas les considérer comme des œuvres d'art", ajoute Konrad Polthier - qui, par ailleurs, dénie en ce qui le concerne toute intention de création. A ses yeux, la beauté de ces formes est "absolue" - comparable à celle, naturelle, des végétaux ou des minérauxminéraux - et non l'expression d'une subjectivité ou d'un message.

    3 - Communication :

    <br />Visualisation informatisée du concept de Surface de Boy à point triple , découvert en 1902. Cet objet mathématique étrange, doté d'une seule face et non orientable (tout comme le ruban de Moebius dont il est une extension), constitue une modélisation de ce que les mathématiciens appellent le "plan projectif". Ce dernier peut être comparé, intuitivement, à une représentation plane de l'ensemble des droites convergeant de tous les points d'une sphère vers un "œil" situé en son centre. Ceci s'apparente à une résolution analytique du fameux problème géométrique de la sphère renversée (dont la face interne aurait été échangée avec sa face externe).<br />&copy; Konrad Polthier, T-U Berlin

    Visualisation informatisée du concept de Surface de Boy à point triple , découvert en 1902. Cet objet mathématique étrange, doté d'une seule face et non orientable (tout comme le ruban de Moebius dont il est une extension), constitue une modélisation de ce que les mathématiciens appellent le "plan projectif". Ce dernier peut être comparé, intuitivement, à une représentation plane de l'ensemble des droites convergeant de tous les points d'une sphère vers un "œil" situé en son centre. Ceci s'apparente à une résolution analytique du fameux problème géométrique de la sphère renversée (dont la face interne aurait été échangée avec sa face externe).
    © Konrad Polthier, T-U Berlin

    "UtilitaireUtilitaire", la visualisation permet également une meilleure compréhension des mathématiques et constitue un moyen de briser le fossé entre l'abstraction et ses applicationsapplications pratiques (en révélant notamment les notions fondamentales qui les sous-tendent). C'est d'ailleurs souvent l'usage pédagogique des images mathématiques, plus que ses ambitions esthétiques, qui sont évoqués par les scientifiques. Manuel Arala Chaves, de la Faculté des Sciences de Porto, distingue néanmoins deux aspects. "Tout d'abord, de belles images attirent l'attention, soulèvent l'intérêt et peuvent ensuite mener à une réflexion et à une curiosité sur des concepts et des résultats mathématiques. Mais en outre, dans de certains cas, les images elles-mêmes suggèrent déjà des idées mathématiques ou, au moins permettent, de les illustrer d'une façon géométrique ."

    Manuel Arala Chaves est à l'origine de plusieurs expositions, notamment Matematica Viva qui s'est tenue à Lisbonne en 2000. Un point important est celui du public-cible. Cette exposition s'adressait à tout le monde et ce fut heureusement ainsi. Nous avons reçu des groupes scolaires aussi bien que des visiteurs qui désiraient approfondir ce qu'ils découvraient. Les modules, en effet, étaient conçus pour offrir différents niveaux de lecture et être décryptés selon son intérêt et sa culture mathématique.

    Quand j'étais jeune, j'ai fait plusieurs visites au Deutsches Museum en Allemagne et au Palais de la Découverte à Paris. Elles m'ont beaucoup marqué, mais j'ai toujours estimé que les mathématiques y étaient sous-représentées, et que cet oubli n'était pas dû au caractère spécifique de la mathématique.

    4 - Jeux de piste :

    <br />Transformation d'une surface caténoïde en surface hélicoïde. Déjà conceptualisée par le mathématicien Euler en 1740, puis par Joseph Plateau au XIXème siècle, cette forme géométrique est par définition une surface dite minimale , en forme de "diabolo", comprise en ceux cercles superposés. Elle correspond, sur le plan physique, à la forme stable que prendra un film de savon étiré entre les deux cercles, de façon à ce que l'énergie de tension appliquée au film soit minimalisée. L'analyse mathématique complexe des surfaces minimales n'a été formalisée que cent ans plus tard. On peut ainsi transformer, à surface constante, un caténoïde en hélicoïde.<br />&copy; Konrad Polthier, T-U Berlin

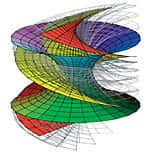
    Transformation d'une surface caténoïde en surface hélicoïde. Déjà conceptualisée par le mathématicien Euler en 1740, puis par Joseph Plateau au XIXème siècle, cette forme géométrique est par définition une surface dite minimale , en forme de "diabolo", comprise en ceux cercles superposés. Elle correspond, sur le plan physique, à la forme stable que prendra un film de savon étiré entre les deux cercles, de façon à ce que l'énergie de tension appliquée au film soit minimalisée. L'analyse mathématique complexe des surfaces minimales n'a été formalisée que cent ans plus tard. On peut ainsi transformer, à surface constante, un caténoïde en hélicoïde.
    © Konrad Polthier, T-U Berlin

    Manuel Arala Chaves a également travaillé et adapté, pour le Portugal, l'exposition Symétrie et jeux de miroirsmiroirs conçue par l'équipe du département de mathématique de l'Université de MilanMilan. Celle-ci a, depuis lors, lancé Matemilano, une seconde aventure particulièrement originale. Quatre grands thèmes (la topologie, massimi e minimi, la vision et la symétrie) sont expliqués à partir de la ville même. L'architecture, la sculpture, la peinture permettent de se glisser dans la géométrie, la perspective, la théorie des nœuds, etc. Les mosaïques romaines, la peinture de la Renaissance, le plan même de la ville, les rosacesrosaces gothiques du Duomo, toutes les époques se prêtent au jeu. "Dans ces deux expositions, nous avons donné une large part aux images et nous sommes fermement convaincus que cette beauté joue un rôle important dans la communication des mathématiques, notamment envers les jeunes et les personnes d'origine culturelle différente", estime Maria Dedo, l'une des chevilleschevilles ouvrières de cette initiative. Une initiative qui prend également en compte cette dimension des mathématiques, qui ne s'apparente plus au domaine du beau mais à celui du jeu. Avec ses problèmes et ses énigmes, la mathématique nous emmène sur de joyeux chemins de traverse. Il suffit - comme le montre Matemilano - d'un papier quadrillé, d'un bout de corde ou de quelques allumettesallumettes pour en faire l'expérience ludique.