Qu'est ce qu'un arbre gracieux ?

En mathématiques, un arbre est constitué de nœuds reliés par des arêtes. Un peu comme dans les arbresarbres généalogiques, chaque nœud a ou non des fils et un nœud est la racine de tous. En voici donc un, pourvu de six nœuds et cinq arêtes (la racine est celui au-dessus).

 

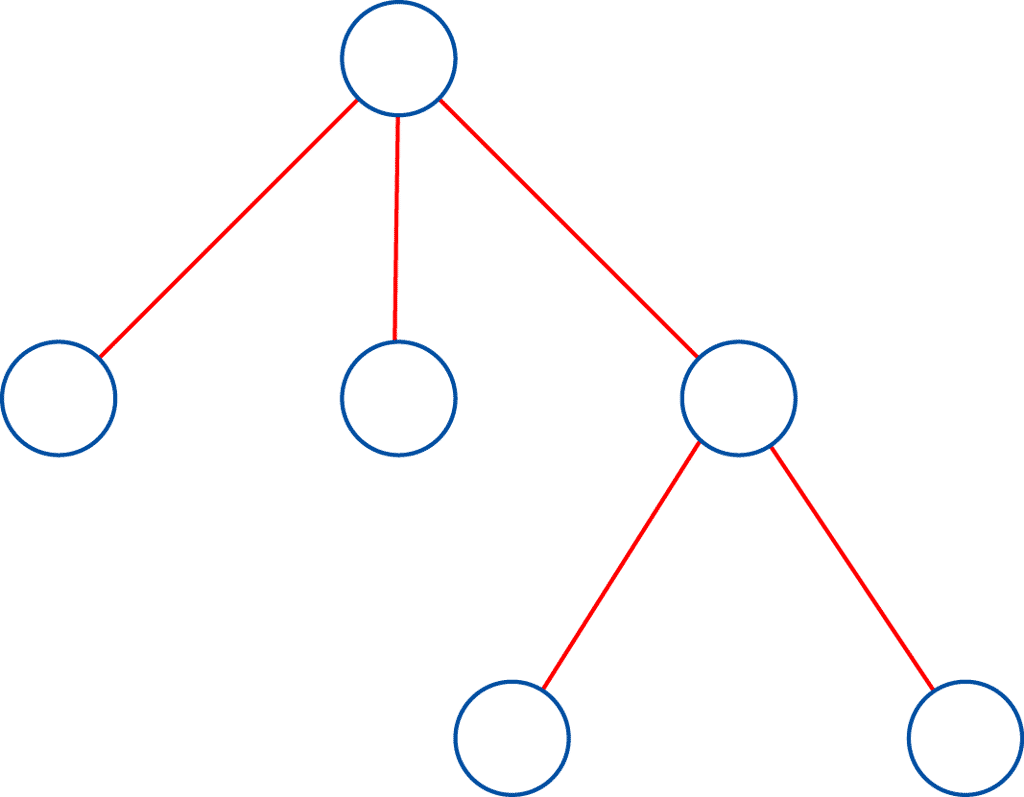
Cet arbre sera considéré comme gracieux si on peut numéroter les nœuds de 0 à 5 et les arêtes de 1 à 5 de sorte que le numéro de chaque arête soit égal, au signe près, à la différence des numéros des nœuds qui la limitent.

Question : cet arbre est-il gracieux ?

Réponse : oui, comme le montre l'étiquetage (ci-dessous).

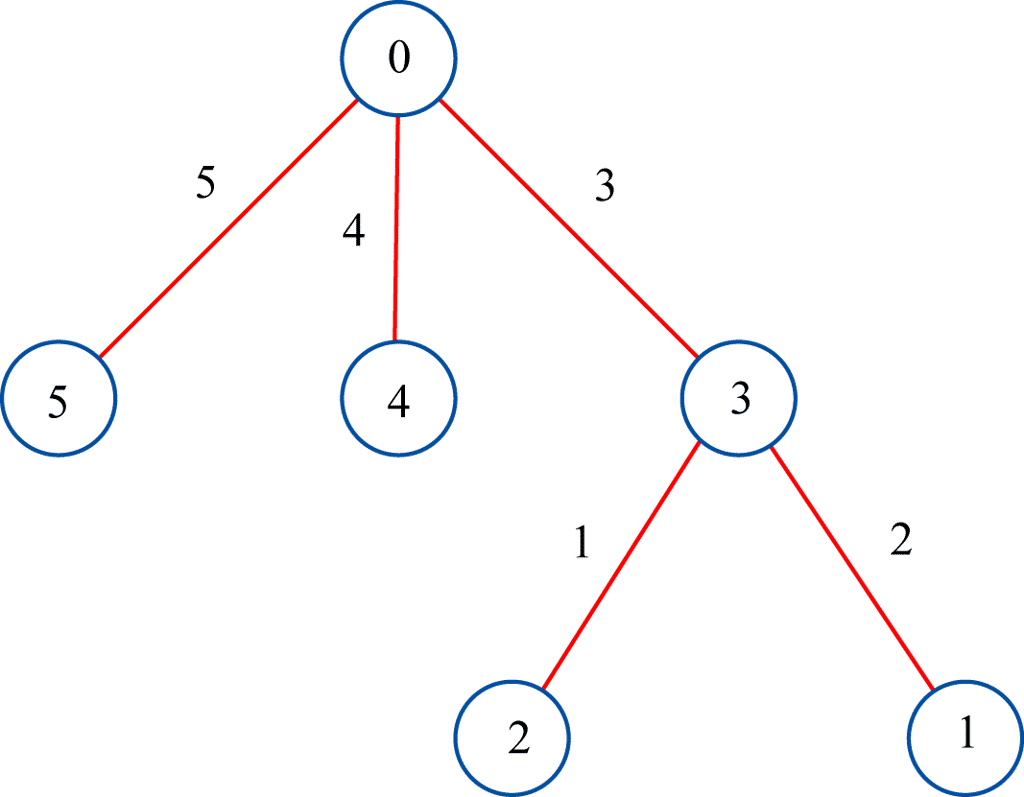
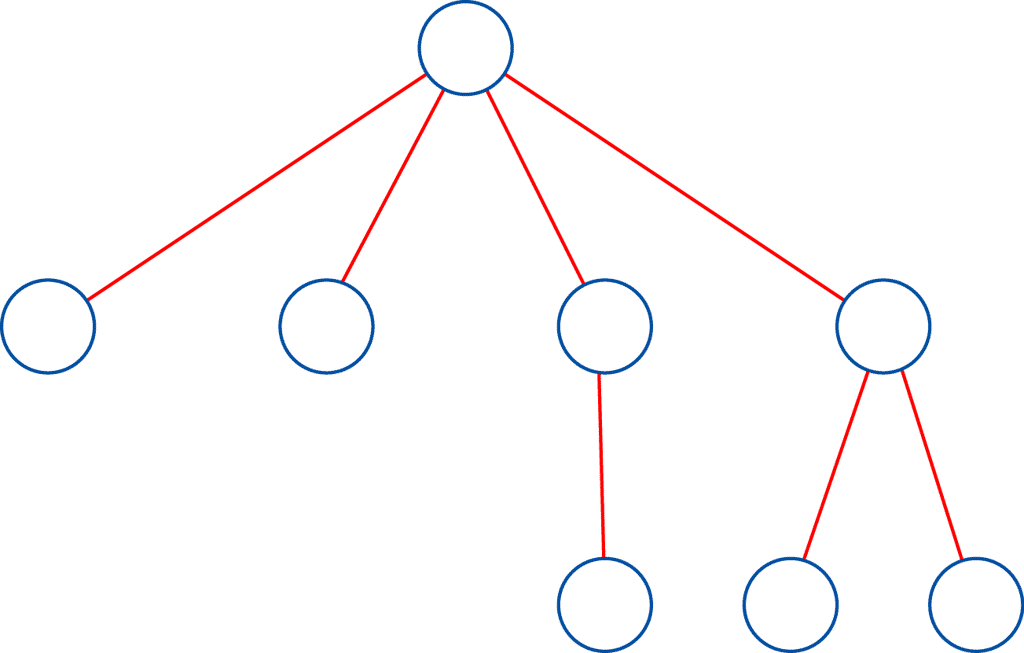
Question : l’arbre suivant est-il gracieux ?

Réponse : oui, comme le montre l'étiquetage (en dessous).  

 

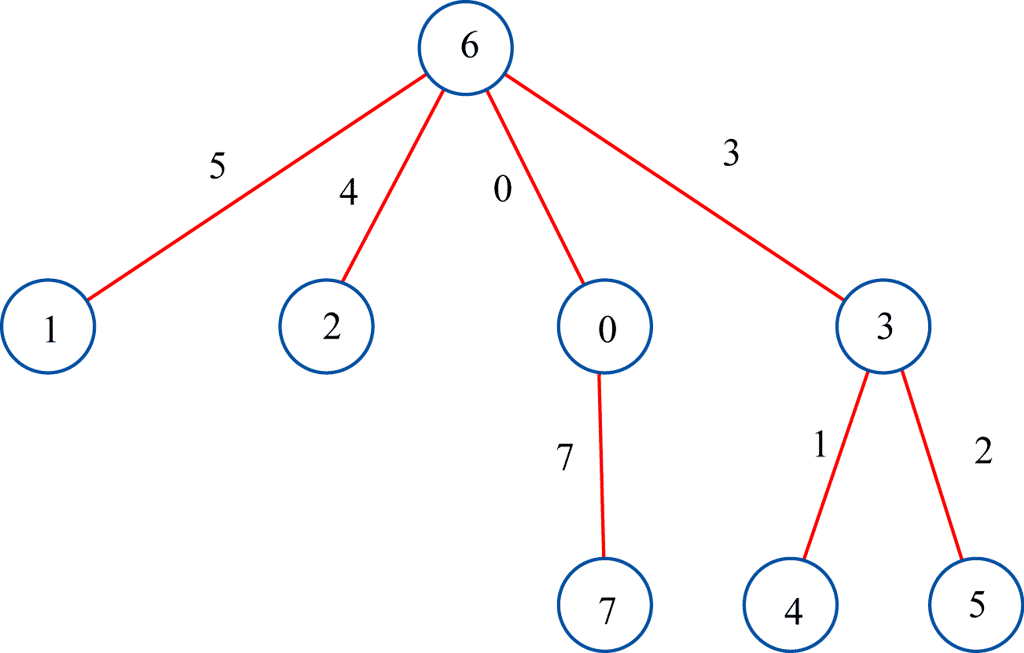
Une conjecture vieille de 50 ans

En 1967, Alexander Rosa, un mathématicien slovaque a conjecturé que tout arbre était gracieux sans pouvoir le démontrer. La question a fait l'objet d'énormément de recherches depuis, mais personne n'a réussi à démontrer que c'était vrai ou que c'était faux. On a seulement réussi à démontrer, grâce à l'utilisation d'ordinateurs puissants, que tous les arbres ayant au plus 35 nœuds sont gracieux.

Une question loufoque ?

Si vous pensez que cette recherche est complètement gratuite et sans applicationsapplications possibles, dites-vous que les réseaux sont représentés par des arbres ou plus généralement des graphes et que la question de l'étiquetage des nœuds et des arêtes a son importance.