au sommaire
La théorie de Maxwell enseigne que de la lumière est émise lorsque des charges sont accélérées, c'est le cas par exemple avec un électron effectuant un mouvement d'oscillation autour de sa position d'équilibre. Il se met à perdre son énergie au profit de celle du champ électromagnétique. En première approximation, un corps solidesolide chauffé peut donc être considéré comme une collection d'électrons effectuant des mouvements oscillants autour d'un centre fixe dans le solide.
Le champ électromagnétique lui-même est défini par le fait qu'il exercera une force sur un électron test placé au bout d'un ressort en un point de l'espace. Le système {corps matériel + champ électromagnétique} peut donc alors se représenter comme un ensemble d'oscillateurs harmoniques couplés.
On est donc en présence d'un système mécanique.
Or, les lois de la thermodynamiquethermodynamique à la fin du XIX ième siècle étaient en train d'être réduites aux lois de la mécanique à l'aide d'hypothèses issues du calcul des probabilités. La théorie cinétique des gazgaz de Clausius, Maxwell et Boltzmann interprétait la chaleurchaleur comme une forme d'énergie mécanique, associée à l'agitation des moléculesmolécules d'un gaz, et la température, à la mesure de cette agitation moléculaire.
En utilisant les principes de ce qu'on appelle la mécanique statistique, le mouvement d'un système mécanique avec un grand nombre de degrés de liberté, convenablement reformulé dans ce que l'on désigne par l'espace des phasesespace des phases d'un système mécanique, devenait alors similaire à celui des molécules dans un gaz.
De même que Maxwell avait introduit une distribution de probabilités donnant à l'équilibre thermodynamique la probabilité de trouver des particules du gaz ayant en moyenne une certaine énergie cinétiqueénergie cinétique, de même, lorsqu'on considérait un système physiquephysique pouvant posséder une certaine énergie Ei, où i désigne aussi bien une série discrète que continue d'états d'énergie pour ce système, on pouvait définir une distribution de probabilités Pi telle que:
avec
où TT est la température thermodynamiquetempérature thermodynamique et
est une constante définie par la condition évidente que la somme des probabilités soit égale à 1.
L'inverse de cette constante se note aussi Z et on l'appelle la fonction de partitionpartition, ou encore la somme des états, en mécanique statistique.
La distribution de probabilités elle-même est connue sous le nom de distribution de Maxwell-Boltzmann, plus précisément et plus généralement aussi sous le nom de distribution de Gibbs en mécanique statistique classique.
Les notions de chaleur, température, entropieentropie, qui sont fondamentales et universelles en thermodynamique classique, trouvaient de cette façon une interprétation et la raison de leur universalité.
Cela supposait toutefois de croire au caractère atomique de la matièrematière dans une large part, mais cela impliquait alors que l'UniversUnivers était constitué de deux entités hétérogènes.
- la matière elle-même, que l'on pouvait décrire par un système discret de coordonnées de positions et de vitessesvitesses généralisées de la mécanique analytique
- le champ électromagnétique, qui, bien que pouvant se décrire sous la forme d'un système mécanique à partir d'un lagrangienlagrangien nécessitait quand même un nombre infini de degrés de liberté en raison de son caractère continu. La racine du problème que vont rencontrer les physiciensphysiciens est précisément ici comme on va le voir.
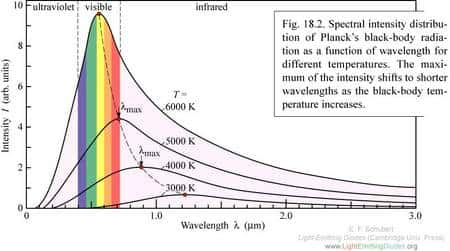
Un théorèmethéorème fondamental de la mécanique statistique, et qui sera au coeur de l'énigme soulevée par la théorie du corps noircorps noir, est celui de l'équipartition de l'énergie pour un système thermodynamique à l'équilibre.
Voyons voir son contenu dans les grandes lignes.
Soit
un hamiltonienhamiltonien avec coordonnées de positions et d'impulsions généralisées qn et pn décrivant, par exemple, l'énergie totale E d'un gaz de molécules ou une collection d'oscillateurs à une température T.
En général, H fait intervenir une somme de termes de la forme
et
Ce qui donne
Le théorème indique alors, qu'en moyenne, chacun de ces termes vaut où
est la constante de Boltzmannconstante de Boltzmann.
Les considérations précédentes ne sont qu'un survolsurvol en haute altitude, et ne prétendant pas à la rigueur, des idées et formules de la mécanique statistique. Il ne s'agit que de donner quelques éléments pour comprendre les problèmes auxquels ont été confrontés les physiciens classiques. Le lecteur voulant vraiment avoir une compréhension solide et rigoureuse de la mécanique statistique devra se reporter à la référence suivante par exemple :
où les formules exactes et les conditions rigoureuses de leur dérivation et applicationsapplications sont exposées. La partie traitant du corps noir en cosmologiecosmologie comporte aussi des liens intéressant et solides sur ces sujets.