Les lois de Kirchhoff, Wien, Stefan-Boltzmann

Vers la fin du XIX^ième siècle, la physique classique semble à beaucoup un monument presque complètement achevé. Les grands principes de l'Univers ont été décryptés, et il ne reste plus que quelques coefficients numériquesnumériques dans les équations à déterminer expérimentalement. Bien sûr, reste encore le problème mathématique de déduire des principes et des équations de la physique classique tous les aspects du monde physique. Mais cela, pour les physiciensphysiciens de l'époque suivant le programme lancé par Descartes quelques siècles plus tôt, c'est la tâche des générations futures.

Il reste quand même deux petites anomaliesanomalies, comme le pape de la physique de l'époque, Lord Kelvin, le mentionnait dans une de ses conférences. La première est bien connue, c'est le résultat négatif de l'expérience de Michelson-Morley, et la seconde, les contradictions et les impasses rencontrées lorsque l'on cherche à déduire des équations de Maxwell, et des principes de la thermodynamiquethermodynamique statistique, les lois du rayonnement d'un corps chauffé.

L'expérience de la vie de tous les jours nous enseigne que lorsqu'on porteporte un corps à une température de plus en plus haute, il se met à rayonner de plus en plus de lumièrelumière et change de couleurcouleur. De même, le rayonnement émis par un corps chaud chauffe un corps plus froid, il suffit de penser à l'action du SoleilSoleil.

La thermodynamique étant la science des transformations de l'énergieénergie, elle doit avoir son mot à dire sur les lois déterminant la quantité de lumière produite par un corps chauffé, ainsi que sur la composition spectrale de cette lumière.

Si l'on considère un ensemble de corps chauffés à des températures différentes, placés dans une enceinte avec des parois parfaitement réfléchissantes, l'expérience montre que les plus froids se réchauffent et les plus chauds se refroidissent jusqu'à atteindre une température uniforme.

L'ensemble constitue alors un système en équilibre thermique ou encore thermodynamique : une situation identique advenant au bout d'un certain temps avec un glaçon plongé dans de l'eau par exemple.

Comme on va le voir, le but des physiciens de l'époque était de comprendre et de décrire le rayonnement précédent à l'équilibre thermique. L'une des étapes les plus importantes pour cela fut la découverte des lois de Kirchhoff

A) Les lois de Kirchhoff

 
Gustave Kirchhoff 1824-1887

Les lois du rayonnement de Kirchhoff sont parmi les plus belles illustrations de la puissance et de la généralité des raisonnements et des principes de la thermodynamique classique. On comparera utilement leurs dérivations avec celles de l'entropieentropie, du rendement des machines réversiblesréversibles, et de la notion de température thermodynamiquetempérature thermodynamique même telles que Feynman et Fermi  les ont exposées dans leurs cours sur la chaleurchaleur.

Considérons donc à nouveau l'enceinte précédente, parfaitement réfléchissante et isolante, contenant une série de corps quelconques à  différentes températures. Au bout d'un moment, un équilibre thermique se produit et aussi bien les parois de l'enceinte que les corps se retrouvent à une même température. Le rayonnement lui-même dans l'enceinte se trouve avoir la même température que les corps à ce moment là, et l'on peut définir la densité d'énergie spectrale de ce rayonnement par unité de volumevolume et bande de fréquencefréquence.

Ce qu'on pourrait appeler la première loi de Kirchhoff est que la fonction définissant la densité d'énergie spectrale du rayonnement dans l'enceinte ne peut être qu'une fonction dépendant uniquement de la température.

Si ce n'était pas le cas, la fonction définissant cette densité devrait dépendre des caractéristiques des corps dans l'enceinte ainsi que des parois de celle-ci. Mais alors, en mettant en contact deux telles enceintes à la même température et avec des corps différents, un transfert d'énergie se produirait de l'une à l'autre permettant d'extraire du travail avec une source monotherme : une contradiction flagrante avec le second principe de la thermodynamiquesecond principe de la thermodynamique.

La thermodynamique nous conduit donc à la découverte de l'existence d'une fonction universelle , caractérisant le rayonnement à l'équilibre thermique et ne dépendant que de la température et de la fréquence de ce rayonnement.

Considérons maintenant un seul corps dans l'enceinte précédente et soit   et le pouvoir absorbant et le pouvoir émissif d'un corps à la fréquence .

On peut alors montrer, qu'en raison de la conservation de l'énergie on doit nécessairement avoir la relation suivante.

  

C'est évident si l'on remarque que les fonctions précédentes sont positives et qu'un corps ne peut émettre plus d'énergie qu'il n'en absorbe, et inversement, de lui-même lorsque l'on est à l'équilibre. C'est ce qu'on pourrait appeler la seconde loi de Kirchhoff du rayonnement thermiquerayonnement thermique.

Nous arrivons maintenant au résultat le plus remarquable et le plus spectaculaire.

Le rapport précédent est, on l'a vu, une fonction universelle.

Soyons malins, prenons un corps noircorps noir, donc parfaitement absorbant, et tel que vaut 1. Le pouvoir émissif de ce corps est donné par la fonction  (De black=noir en anglais) mais comme vaut 1, cette fonction s'identifie avec la fonction .

On aura donc:

Quel que soit le corps émettant de la lumière, à l'équilibre thermodynamique, la formule donnant la répartition de l'énergie rayonnée par bande de fréquence sera celle d'un corps noir !

Bien sûr, les corps ne sont jamais exactement des corps noirs, et surtout, ils ne sont pas toujours en équilibre thermodynamique avec un rayonnement. Il n'en restera pas moins que l'on aura toujours, à l'équilibre thermodynamique, une loi reliant absorptionabsorption et émissionémission de ce corps à une fréquence donnée avec ce qu'on appellera désormais la loi du corps noir.

Les physiciens classiques vont alors se concentrer sur la dérivation précise de cette loi universelle du rayonnement thermique.

Remarquons au passage qu'il est facile de réaliser un corps noir, ou tout au moins se rapprochant avec une excellente précision de celui-ci. En effet, il suffit de construire une enceinte creuse, comme une sphère, aux parois uniformément chauffées. Un rayonnement à l'équilibre thermique se produira de lui-même et, en perçant un petit trou dans cette enceinte, on peut vérifier que le spectrespectre obtenu suit bien les lois du rayonnement d'un corps noir comme les suivantes.

B) Lois de Wien et de Stefan-Boltzmann

wilhelm Wien 1864-1928

Les ressources de la thermodynamique n'étaient pas encore épuisées. Si l'on considère le rayonnement thermique dans une enceinte dont une paroi est mobilemobile, alors il est possible de comprimer le rayonnement tout comme un gazgaz.

Wilhelm Wien, en se basant sur les équations de Maxwell, l'effet Dopplereffet Doppler changeant la fréquence du rayonnement dans l'enceinte par réflexion sur le piston mobile comprimant le rayonnement, et bien sûr les lois de la thermodynamique contraignant les transformations du travail mécanique en chaleur et inversement, a alors dérivé la formule suivante en 1893.

 

Etant elle aussi basée sur des raisonnements thermodynamiques, cette forme est universelle. Elle ne dépend pas des hypothèses particulières liées aux mécanismes d'émissions du rayonnement par un corps matériel, mais juste des équations de Maxwell et des deux principes de la thermodynamique.

Deux autres lois s'en déduisent aussitôt.

On peut faire une somme de l'énergie rayonnée sur tout le spectre, en intégrant, pour obtenir la densité d'énergie totale u du rayonnement à l'équilibre thermique. On obtient la fameuse loi de Stefan-Boltzmann qui avait déjà été obtenue par un autre raisonnement en 1884:

Cette densité d'énergie est reliée à la quantité d'énergie qu'émet, par unité de surface  et par unité de temps t, un corps noir, laquelle est donnée par la formule ci-dessous:

 

Une surface A aura donc une luminositéluminosité totale donnée par:

Enfin, si l'on exprime la loi du corps noir en fonction de la longueur d'ondelongueur d'onde du rayonnement, et que l'on cherche le maximum d'émission à une température donnée, on démontre que celui-ci se trouve à une longueur d'onde  vérifiant ce qu'on appelle la loi du déplacement de Wien.

 

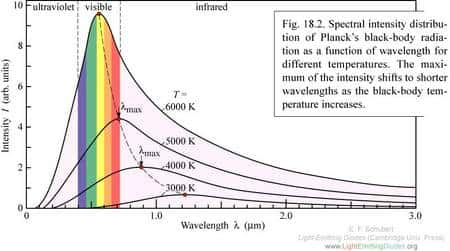
Sur la figure ci-dessous, on a représenté la courbe expérimentale de la distribution spectrale du corps noir à différentes températures mais en fonction, non plus de la fréquence, mais de la longueur d'onde.

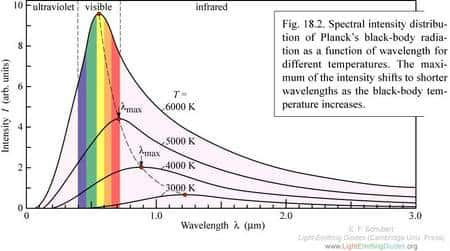
On comparera utilement cette courbe avec celle de la répartition du nombre de particules possédant une vitessevitesse particulière (et donc une énergie cinétiqueénergie cinétique) telle que la donne la loi de Maxwell-Boltzmann en théorie cinétique des gaz.

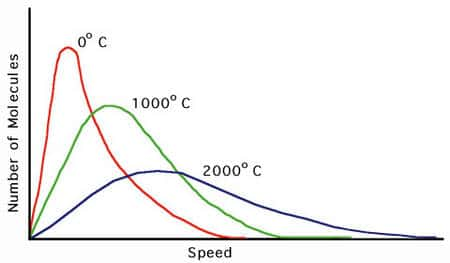
(Crédit : Whashington University).

En utilisant seulement les lois de la thermodynamique classique (sans théorie cinétique ni hypothèse atomique) et les lois de l'optique, c'est à peu près tout ce qu'il était possible de faire. La thermodynamique classique était cependant en passe d'être révolutionnée complètement par la mécanique statistique de Maxwell-Boltzmann et surtout de Gibbs-EinsteinEinstein. C'est son applicationapplication au problème du corps noir que nous allons étudier maintenant.

Pour en savoir plus : cours de Claude Aslangul sur l'ancienne théorie des quanta.