au sommaire
Un corps noir est un objet idéal qui absorbe toute l'énergie électromagnétique (lumière) incidente, quelle que soit la longueur d'onde ou l'angle d'incidenceincidence. Il ne réfléchit ni ne transmet aucune énergie, ce qui le rend parfaitement noir lorsqu'il est à une température plus basse que son environnement. Cependant, lorsqu'il est chauffé, un corps noir émet un rayonnement électromagnétique appelé « rayonnement du corps noir ».
Les corps noirs, comme tous les autres corps, émettent des radiations comprises dans un spectre caractéristique qui dépend exclusivement de la température absolue. À chaque valeur de la température correspond une longueur d'onde dominante.
Découverte du corps noir et de ses propriétés
L'histoire de la découverte du corps noir remonte au milieu du XIXe siècle, lorsque les physiciensphysiciens ont commencé à étudier la nature du rayonnement électromagnétique émis par les objets chauds. En 1859, le physicien allemand Gustav Kirchhoff a proposé l'existence d'un objet idéal, qu'il a appelé « corps noir », capable d'absorber complètement tous les rayonnements électromagnétiques incidents, quelle que soit leur longueur d'onde. Kirchhoff a également suggéré que le spectre d'émissionspectre d'émission d'un corps noir dépendait uniquement de sa température. Cependant, ce n'est qu'en 1893 que le physicien allemand Wilhelm Wien a découvert la loi de déplacement de Wien, qui décrit la relation entre la température d'un corps noir et la longueur d'onde à laquelle il émet le plus d'énergie.
En 1900, le physicien allemand Max PlanckMax Planck a développé une théorie pour expliquer le spectre d'émission du corps noir, qui a conduit à la naissance de la mécanique quantique. Planck a proposé que l'énergie électromagnétique était quantifiée, c'est-à-dire qu'elle ne pouvait être émise ou absorbée que sous forme de paquetspaquets discrets appelés « quanta ». En utilisant cette hypothèse, Planck a pu dériver la loi de rayonnement du corps noir, qui décrit la distribution spectrale de l'énergie émise par un corps noir en fonction de sa température. Cette hypothèse a conduit à la naissance de la mécanique quantique et a valu à Planck le prix Nobel de physiquephysique en 1918.
Dans les années qui ont suivi, d'autres physiciens ont poursuivi les recherches sur le corps noir et ses propriétés. Albert EinsteinEinstein a utilisé la loi de rayonnement du corps noir pour expliquer l'effet photoélectriquephotoélectrique, ce qui lui a valu le prix Nobel de physique en 1921.
Les lois du corps noir
Les lois du corps noir sont un ensemble de lois qui décrivent le comportement du rayonnement électromagnétique émis par un corps noir en fonction de sa température. Les principales lois du corps noir sont les suivantes :
Loi de Planck
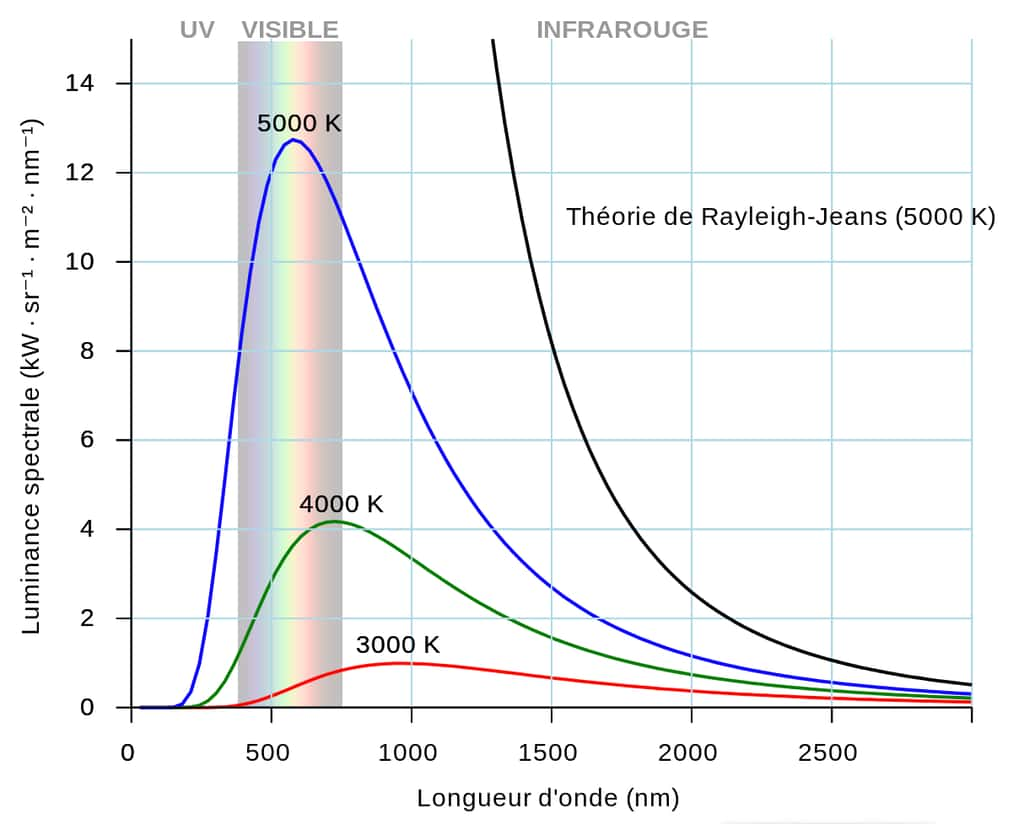
La loi de Planck décrit la distribution spectrale de l'énergie émise par un corps noir en fonction de sa température. Selon la loi de rayonnement du corps noir, l'énergie émise par un corps noir à une température donnée est répartie sur tout le spectre électromagnétique, allant des ondes radio aux rayons gamma. La répartition spectrale de l'énergie dépend de la température du corps noir, de sorte que plus la température est élevée, plus l'énergie est concentrée dans les longueurs d'onde courtes (c'est-à-dire vers le bleu), et moins la température est élevée, plus l'énergie est concentrée dans les longueurs d'onde longues (c'est-à-dire vers le rouge).
La loi de Planck est exprimée mathématiquement par la formule : I(λ,TT) = (2hc²/λ⁵) * (1/(exp(hc/(λkT))) - 1)) où I est l'intensité du rayonnement, λ est la longueur d'onde, T est la température, h est la constante de Planckconstante de Planck, c est la vitesse de la lumièrevitesse de la lumière et k est la constante de Boltzmannconstante de Boltzmann.
Loi de Wien
La loi de Wien décrit la relation entre la température d'un corps noir et la longueur d'onde à laquelle le rayonnement est le plus intense. Elle énonce que la longueur d'onde à laquelle le rayonnement du corps noir atteint son maximum d'intensité est inversement proportionnelle à la température du corps noir. La loi de Wien est exprimée mathématiquement par la formule : λmax = b/T où λmax est la longueur d'onde à laquelle le rayonnement est le plus intense, b est la constante de Wien et T est la température.
Loi de Stefan-Boltzmann
La loi de Stefan-Boltzmann décrit la puissance totale rayonnée par unité de surface d'un corps noir en fonction de sa température. Elle énonce que la puissance rayonnée par unité de surface est proportionnelle à la quatrième puissance de la température absolue du corps noir. La loi de Stefan-Boltzmann est exprimée mathématiquement par la formule : P = σT⁴ où P est la puissance rayonnée par unité de surface, σ est la constante de Stefan-Boltzmann et T est la température.
Ces lois du corps noir sont fondamentales pour comprendre le comportement du rayonnement électromagnétique et ont des applicationsapplications importantes dans de nombreux domaines, notamment en astrophysique, en physique des hautes énergies, en ingénierie et en science des matériaux.
Des exemples de corps noir dans la nature
Un corps noir parfait n'existe pas dans la nature, car il est impossible de créer un objet capable d'absorber complètement tous les rayonnements électromagnétiques incidents, quelle que soit leur longueur d'onde. Cependant, il existe des objets qui se rapprochent beaucoup de cette idéalisation.
Un exemple courant de corps noir approximatif est un trou noir. Les trous noirstrous noirs sont des objets célestes extrêmement denses dont la gravitégravité est si forte que rien, pas même la lumière, ne peut s'en échapper. Les trous noirs absorbent donc tout le rayonnement électromagnétique incident, ce qui en fait des corps noirs presque parfaits.
Le corps noir en laboratoire
Dans la nature, il n'existe pas de corps avec les caractéristiques requises, mais en laboratoire, il est possible de construire des modèles qui, dans des conditions déterminées, sont capables d'en simuler fidèlement le comportement. Toute enceinte isotherme, fermée à l'exception d'une très petite ouverture, joue le rôle d'un corps noir.
Les physiciens peuvent créer des corps noirs approximatifs en utilisant des cavités réfléchissantes par exemple une enceinte fermée dont les parois sont recouvertes d'un matériaumatériau réfléchissant, comme de l'aluminiumaluminium ou de l'argentargent. Lorsque la cavité est chauffée, les parois réfléchissantes absorbent et réémettent le rayonnement électromagnétique à l'intérieur de la cavité, jusqu'à ce que l'équilibre thermique soit atteint. À ce stade, la cavité émet un rayonnement électromagnétique qui suit la loi de rayonnement du corps noir.
En pratique, les cavités réfléchissantes ne sont pas des corps noirs parfaits, car une partie du rayonnement électromagnétique incident peut être réfléchie plutôt qu'absorbée. Cependant, en utilisant des matériaux réfléchissants très efficaces et en minimisant les pertes d'énergie, il est possible de créer des cavités réfléchissantes qui se rapprochent beaucoup de l'idéal du corps noir.
Le corps noir en physique
Le concept de corps noir est un outil important en physique, en particulier dans les domaines de la thermodynamiquethermodynamique, de l'optique et de l'astronomie.
Voici quelques-unes des utilisations et des applications importantes du concept de corps noir :
- Lois du rayonnement : le corps noir est un objet idéal qui permet de décrire les propriétés du rayonnement électromagnétique en fonction de la température. Les lois du rayonnement du corps noir, telles que la loi de Planck, la loi de Wien et la loi de Stefan-Boltzmann, sont fondamentales pour comprendre le comportement du rayonnement thermiquerayonnement thermique.
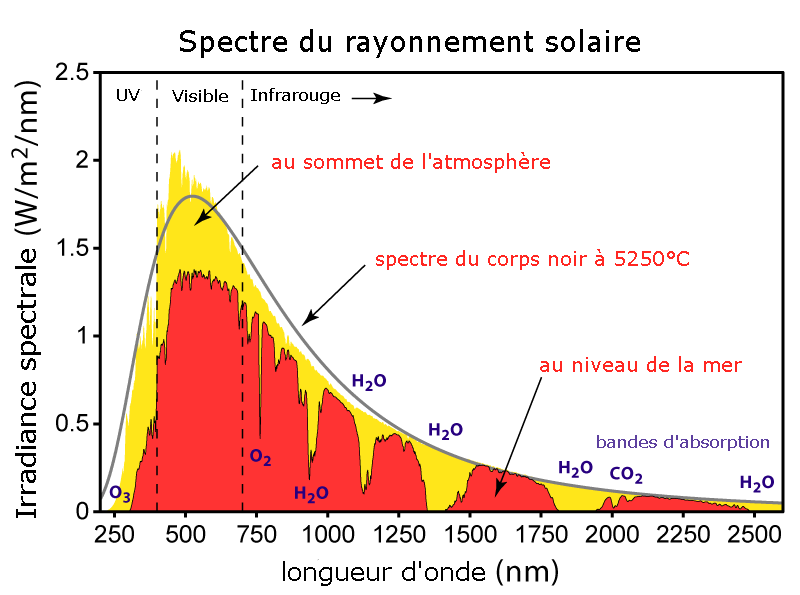
- Spectroscopie : le spectre du rayonnement émis par un corps noir dépend uniquement de sa température. Cette propriété permet aux scientifiques d'utiliser la spectroscopie pour déterminer la température des objets célestes, tels que les étoilesétoiles et les galaxiesgalaxies.
- ModélisationModélisation de l'émission thermique : le concept de corps noir est utilisé pour modéliser l'émission thermique de divers objets, tels que les bâtiments, les véhicules et les équipements électroniques. Cela permet de concevoir des systèmes de refroidissement et d'isolationisolation plus efficaces.
- Étalonnage des instruments : les sources de rayonnement du corps noir sont utilisées pour étalonner les instruments de mesure de rayonnement, tels que les spectromètresspectromètres et les radiomètresradiomètres. Cela garantit que les mesures sont précises et fiables.
- Recherche en physique quantiquephysique quantique : le rayonnement du corps noir a joué un rôle clé dans le développement de la physique quantique. L'étude du rayonnement du corps noir a conduit à la découverte des quanta de lumière, ou photonsphotons, et a ouvert la voie à la mécanique quantiquemécanique quantique.