Le rayonnement des trous noirs comme clé de la physique du XXIième siècle

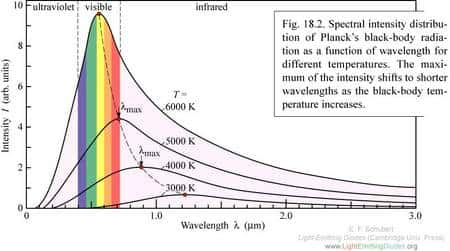
La saga du corps noir n'est pas terminée. Tout comme le rayonnement thermique et la formule de PlanckPlanck ont été à l'origine de la théorie quantique, le rayonnement des trous noir pourrait bien être à l'origine d'une nouvelle révolution de la physique, celle du XXI ième siècle.

L'entropie est en effet une mesure du degré de désordre d'un système physique et elle se calcule avec les différents micro-états responsables d'un macro-état. Ainsi, l'entropie d'un gaz parfaitgaz parfait décrit macroscopiquement par sa température et sa pressionpression, est reliée au nombre d'états d'énergieénergie possibles des particules le composant, les micro-états, et correspondant à son macro-état décrit par les deux paramètres précédents.

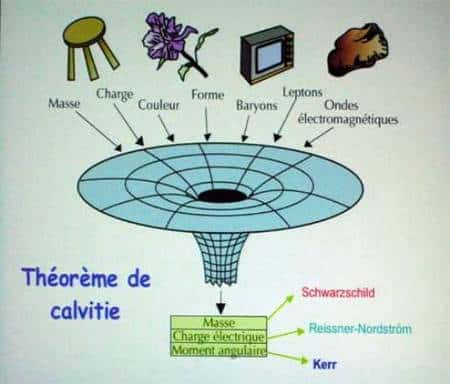
Or, il existe une série de théorèmesthéorèmes en relativité généralerelativité générale démontrant qu'il ne peut exister que des familles de trous noirs décrits exactement par leur massemasse, leurs charges (électriques et magnétiques) et leur moment cinétiquemoment cinétique. Il ne s'agit pas d'approximation mais de solutions exactes. Un trou noir ne doit donc pas enregistrer et conserver les détails concernant la constitution des objets qu'il absorbe mais uniquement la masse, la charge et le moment cinétique de ceux-ci. John Wheeler a désigné cette propriété par une expression qui allait, là encore, devenir célèbre :"Les trous noirs n'ont pas de cheveux". C'est le "no hair theorem"

Illustration du "no hair theorem" (Crédit : Jean Pierre Luminet).

En ce sens, comme le faisait remarquer le grand astrophysicienastrophysicien et prix Nobel Chandrasekhar, les trous noirs sont les objets les plus simples et les plus parfaits de l'UniversUnivers. Tout comme les particules élémentairesparticules élémentaires, ils ne sont décrits que par un petit nombre de paramètres.

Où sont alors les micro-états à l'origine de l'entropie des trous noirs ?

Une question d'autant plus pressante que d'après la relativité générale et les théorèmes de singularité de Hawking-Penrose-Geroch, tout corps tombant dans un trou noir finit sa course au centre de celui-ci en une singularité de l'espace-tempsespace-temps où toutes formes et compositions porteuses d'informations sont détruites. D'ailleurs, avant même d'arriver à la singularité, les forces de maréeforces de marée seraient tellement fortes que même les quarksquarks confinés dans les hadronshadrons ne pourraient le rester, des protonsprotons seraient ainsi complètement déchiquetés.

Pire, on peut montrer que tant que le trou noir n'atteint pas la température et la taille de Planck, et même en tenant compte des interactions entre les particules émises à l'horizon, le rayonnement reste complètement thermique et décrit par la loi de Planck. Hawking en a alors conclu que le processus d'évaporation des trous noirs détruisait irrémédiablement de l'information. Une conclusion que n'acceptèrent ni les prix Nobel Gerard ‘t Hooft et David GrossDavid Gross, ni Leonard Susskind.

Léonard Susskind (Crédit : Stanford University).

Le prix Nobel de physique G. 't Hooft (Crédit : Soylent Communications).

Pour eux, une telle destruction de l'information impliquerait aussitôt une violation des principes fondamentaux de la mécanique quantiquemécanique quantique incompatible avec les expériences de physique déjà testées, comme une possible violation importante de la conservation de l'énergie.

C’est le fameux paradoxe de l’information !

D'un côté les lois de la mécanique quantique exigent l'apparition du rayonnement Hawking mais de l'autre celui-ci les violerait !

Enfin, l'entropie d'un système physique est normalement reliée au volumevolume d'un système, pas à sa surface. Tout se passe comme si les détails de l'information et de la physique dans un volume de l'espace étaient équivalents à ceux portés par une surface. Un phénomène rappelant ce qui se passe avec les hologrammeshologrammes codant des images en relief sur une plaque. Les degrés de liberté possibles pour un système dans l'espace seraient alors moins nombreux qu'on ne le pensait. Une situation étrangement similaire, d'ailleurs, à celle ayant conduit à l'apparition de la formule de Planck elle-même, avec la quantificationquantification des oscillateurs du champ électromagnétiquechamp électromagnétique réduisant leurs états de mouvementsmouvements possibles.

Toutes ces questions commencent à recevoir des réponses dans le cadre de la théorie des cordesthéorie des cordes qui, si elle représente la bonne approche, serait selon les mots d'Amaldi, la physique du XXI ième siècle tombée par hasard au XX ième siècle.

Illustration d'un diagramme de feynman pour une corde fermée par robbert-dijkgraaf

La dérivation de la formule de Hawking-Bekenstein en utilisant la théorie des cordes, dans le cas de certains trous noirs supersymétriques, par Andrew Strominger et Cumrun Vafa en 1995 a d'ailleurs révolutionné aussi bien l'étude des trous noirs que la théorie des cordes elle-même.

Andrew Strominger

Cumrun Vafa

L'avenir proche confirmera peut-être, comme le pensent certains, que le paradoxe de l'information est l'analogue de la catastrophe ultraviolette et que la théorie du rayonnement thermique des trous noirs est à la gravitation quantiquegravitation quantique ce que la formule de Planck et l'atome de Bohratome de Bohr ont été pour la mécanique quantique elle-même. Une excellente revue de la question de l'entropie des trous noirs et de sa dérivation à partir de la théorie des cordes dans certains cas peut se trouver dans un article de Thibault Damour.

Comme ce dossier en a, on l'espère, convaincu le lecteur, la théorie du rayonnement du corps noir, en apparence un problème anodin de la physique, a changé notre image du monde aussi bien de l'atome que jusqu'à l'Univers lui-même. Ce n'est probablement pas fini.