au sommaire

Le modèle standard : la théorie électrofaible
Les idées que Yang et Mills avaient proposées en 1954 allaient se révéler cruciales dans le développement du fameux modèle standard comportant l'électromagnétisme et les lois des forces nucléaires fortes et faibles.
Le « principe de jauge » revêt toute son importance en 1961, sous l'impulsion des travaux de Salam et Ward, qui proposent alors une méthode générale pour construire une théorie de champs en interaction les uns avec les autres. Selon ce principe, la symétrie de jauge n'est pas seulement une symétrie globale, elle doit être élevée au rang de symétrie locale. Déjà en électrodynamique classique, un potentiel de jauge est introduit, à partir duquel peuvent se déduire les champs électrique et magnétique.

Le prix Nobel Chen Ning Yang et Robert Mills. © AIP
Partons d'une théorie ne contenant que des particules matérielles. Cette théorie possède une invariance globale, la possibilité de choisir arbitrairement la « phase » des fonctions d'ondes phi des particules matérielles. Une fonction d'onde prend des valeurs complexes, et se représente donc comme une « flèche » dans un plan complexe dont les axes correspondent aux parties réelles et imaginaires. La phase d'un nombre complexe correspond à la direction de la flèche le représentant (on se reportera utilement à Lumière et matière : une étrange histoire de R. Feynman). Dire qu'une théorie est invariante sous un changement de phase globale, c'est dire qu'il n'y a pas de direction privilégiée dans ce plan. Lorsqu'on élève cette invariance globale au rang d'invariance locale, on permet à cette direction arbitraire de dépendre de la position dans l'espace du point où la fonction d'onde est évaluée.
En conséquence, de nouveaux termes apparaissent dans les dérivées que l'on effectue sur ces fonctions d'ondes et qui permettent de construire les équations gouvernant les particules. Il est donc nécessaire d'introduire de nouveaux champs pour compenser ces termes supplémentaires, les nouvelles dérivées se transforment alors en « dérivées covariantes ». Ces nouveaux champs correspondent au potentiel de l'électrodynamique.
En mathématiques, on les nomme « connexions » car ils permettent de connaître la variation de la phase d'un point à un autre et ainsi de définir une opération de transport parallèle d'un point à un autre, ce qui est intuitivement semblable à la définition d'un opérateur de dérivation. Physiquement, ils correspondent aux champs des « bosons vecteurs » qui portent l'interaction entre les particules matérielles.
En réalité, cette symétrie de jauge est très contraignante. À première vue, elle impose que toutes les particules soient sans massemasse, aussi bien les particules matérielles que les particules portant les interactions. Il semble donc qu'il n'y ait que peu d'espoir qu'un tel principe gouverne les constructionsconstructions modernes de modèles pour les interactions fondamentales. Et pourtant...
- A - Le mécanisme de Higgs, Brout, Englert
Ici va intervenir un théorèmethéorème important sur les caractéristiques d'équations susceptibles d'être utilisées pour les champs de Yang-Mills, le théorème de Goldstone. Celui-ci indique que pour chaque brisure spontanée de symétrie une particule sans masse doit apparaître. Voyons donc ce qui se cache derrière ce terme « brisure spontanée de symétrie ».
Une image amusante a été proposée par Salam. Considérez une table ronde, prête à recevoir ses convives. Le long du périmètre de cette table alternent régulièrement assiettes et cuillères. Avant le début du repas, la situation est parfaitement symétrique et invariante par rotation. Mais lorsque le premier convive s'assoit, il choisit une cuillère à droite ou à gauche de son assiette. Ensuite, tous les autres convives doivent respecter la même convention que lui, faute de quoi l'un des convives n'aurait pas de cuillère.
On parle de brisure spontanée de symétrie lorsque les lois gouvernant l'évolution d'un système sont invariantes sous une certaine transformation, mais l'état fondamentalétat fondamental (le vide en théorie des champs) ne respecte pas une telle invariance. Comme tous les états sont construits à partir de l'état fondamental, il résulte que la symétrie est cachée.
Anderson découvrit en 1963, dans le contexte des oscillations de plasma et dans un formalisme non relativiste, que le spectrespectre d'une théorie avec brisure spontanée de symétrie peut en fait ne plus contenir ce fameux boson de Goldstone. Ce mécanisme a été ensuite redécouvert peu de temps plus tard, par Higgs, par Englert et Brout, et par Guralnik, Hagen et Kibble (cf. a1, a2).

François Englert, et Robert Brout. © DR
Ces travaux ont permis d'établir que le théorème de Goldstone n'était pas valable pour une symétrie locale. Dans le cas d'une symétrie locale, un calcul rigoureux montre en effet que le degré de liberté associé au boson de Goldstone est absorbé par le boson de jauge, qui acquiert ainsi une masse. De même, le couplage des particules matérielles au champ de Higgs donne un terme analogue à un terme de masse. La masse d'une particule est donc déterminée par l'intensité de son couplage au champ de Higgs.
Illustrons ceci de façon plus concrète, dans une théorie de type Yang-Mills on introduit l'analogue de l'équation du potentiel vecteur du champ électromagnétiquechamp électromagnétique (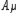
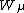
Ce nouveau champ correspond à une connexion et permet de définir une opération de dérivation covariante :
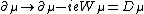
S'il y avait un terme de masse, on aurait une équation de type Proca. Or, on l'a vu, ceci ne peut se faire aussi simplement sans introduire des quantités infinies non renormalisables.
L'astuce est d'introduire un champ scalaire décrivant une particule, le fameux boson de Higgs.
Maintenant, les équations des champs en physiquephysique des particules sont dérivées d'une fonction mathématique appelée lagrangienlagrangien. Il existe, par exemple, un lagrangien pour les équations de Maxwelléquations de Maxwell du champ électromagnétique. On peut voir clairement que lorsqu'on effectue certaines transformations sur les variables de champs celui-ci reste invariantinvariant, et cela implique alors des lois de conservations comme celle de la charge.
On a alors un théorème général pour les lagrangiens d'équations de champ, dit théorème de Noether, qui relie les invariances de ces lagrangiens à des quantités conservées, comme par exemple des isospins pour les équations de Yang Mills.
Lorsqu'on écrit le lagrangien L d'un champ scalaire, on obtient une expression de la forme suivante :
L = 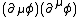
où 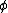
Une transformation de jauge correspond à un déphasage donné dans ce cas simple par :
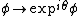
On assure l'invariance du lagrangien du système champ de Higgs+champ de Yang-Mills en utilisant les dérivées covariantes dont on a déjà parlé.
La substitution donne alors :
L= 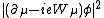
Où l'on a tenu compte du fait que 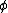
En développant l'expression apparaît « magiquement » le terme :
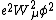
Ainsi lorsque 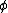
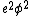
À partir du lagrangien on obtient alors l'équation décrivant le champ de ce boson W.
Elle s'écrit :
On peut montrer que la renormalisabilité de la théorie est assurée et l'on a donc introduit une masse pour nos bosons responsables de forces nucléaires.
C'est tout à fait similaire à l'apparition de masses pour les photonsphotons dans un plasma ou dans les phénomènes de supraconductivitésupraconductivité comme l'effet Meissnereffet Meissner, rien d'étonnant alors à ce que ce soit des gens travaillant en physique de la matièrematière condensée qui en ont eu l'idée.
Un point clé reste à éclaircir, pourquoi le champ 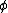
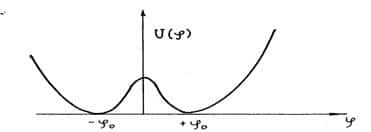
On y voit que l'état d'énergieénergie minimum est donné par 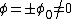
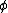
On donne souvent l'exemple de la brusque déformation d'un clou soumis à une pressionpression et c'est cela qui est aussi relié à l'idée d'une brisure spontanée de symétrie.
Des potentiels de la forme indiquée étaient déjà connus dans la théorie du ferromagnétismeferromagnétisme.
Ils décrivent l'orientation des moments magnétiquesmoments magnétiques (liés au spinspin) des atomesatomes, ceux-ci se comportent alors comme des minis aimantsaimants. Lorsque 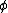
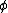
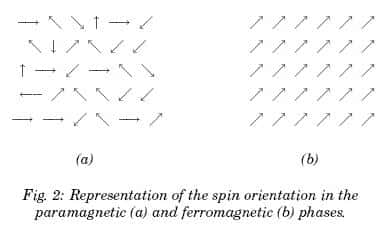
En fait comme on a affaire à un champ complexe pour le champ du boson de Higgsboson de Higgs, 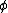
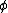
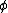
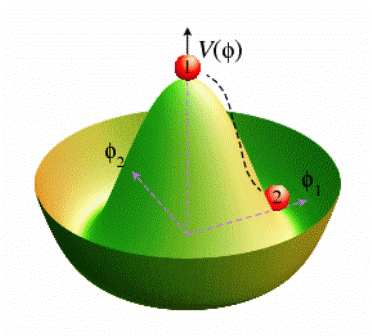
On reconnaît au centre l'état d'équilibre instable du potentiel V où le champ de Higgs s'annule. © Gerard 't Hooft-Scholarpedia
- B - La théorie unifiée de Glashow Salam Weinberg (cf. d3, d4)

Tous prix Nobel en 1979
Le modèle standard décrit de façon cohérente les interactions électromagnétique et nucléaire faible. La recette pour construire une théorie de jaugethéorie de jauge est aujourd'hui bien comprise :
- choisir un groupe de symétrie et rassembler des particules dans des « isospins » associés, on parle alors de multiplets ;
- introduire les bosons de jauge qui portent les interactions et les champs de matière en choisissant leur représentation ;
- ajouter les champs de Higgs afin de générer les masses des bosons vecteurs ;
- définir une dérivation covariante produisant les termes d'interactions entre les champs ;
- choisir alors l'état du vide de telle sorte que son énergie soit minimale. À cette étape cruciale une partie des symétries est spontanément brisée.
Glashow proposa ainsi en 1961 le groupe de jauge SU(2)*U(1) pour unifier électromagnétisme et interaction nucléaire faible. Un modèle similaire fut proposé en 1964 par Salam et Ward.
Enfin Weinberg en 1967 et Salam en 1968 ont synthétisé ces efforts, en incluant le mécanisme de Higgs afin de préserver l'invariance de jauge.

Les particules du modèle standard, les quarks, les leptons et les bosons de jauge. © Fermilab
Remarquez que quarksquarks et leptonsleptons forment trois familles et qu'ils sont groupés par doubletsdoublets d'isospins (ex quark uquark u et d, électronélectron et neutrino électroniqueneutrino électronique).
Il n'était alors pas encore démontré que le modèle ainsi construit était renormalisable (cf. section suivante).
Cette théorie considère que le champ électromagnétique est véhiculé par un photon associé à un potentiel vecteur 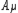
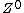
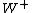
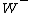
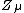
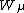
Notons qu'à ce stade le modèle ne contient pas encore la chromodynamique quantiquechromodynamique quantique, qui décrit l'interaction des quarks et des gluonsgluons et est responsable de la cohésion nucléaire.
Il s'agit de l'interaction forteinteraction forte (par opposition à l'interaction faibleinteraction faible, responsable de la désintégration bêtabêta du noyau).
Le groupe employé est ici SU(3), son incorporation fut rapidement faite avec le modèle des quarks et les bosons vecteurs associés que l'on nomme gluons notés g.
Notons également que la gravitationgravitation n'est toujours pas incluse dans le modèle standard. Dans le contexte général de l'origine de la masse et considérant le rôle fondamental de la notion de masse pour les phénomènes gravitationnels, ce problème théorique criant est pour le moins déplaisant.
- C : La révolution 't Hooft (cf. d1, d2)

Gerard 't Hooft devant le détecteur Atlas destiné à découvrir le boson de Higgs. © Cern
Au début des années 70, Gerard ‘t Hooft et Martinus Veltman (prix Nobel de physique 1999) apportent les dernières contributions qui feront de la théorie électrofaiblethéorie électrofaible de Glashow-Salam-Weinberg une théorie opérationnelle.
Il fallait en effet prouver la renormalisabilité de la théorie. C'est ce qu'ils firent en prouvant la possibilité d'éliminer tous les infinis dans toutes les théories de Yang-Millsthéories de Yang-Mills non abélienne massives comportant le mécanisme de Higgs.
Ils firent appel aux techniques mises au point vingt ans plus tôt par Richard FeynmanRichard Feynman l'un des créateurs de l'électrodynamique quantiqueélectrodynamique quantique relativiste, lui aussi prix Nobel avec Schwinger et Tomonaga (1965).

Notamment 't Hooft fit grand usage de la fameuse intégrale de chemin de Feynman, une formulation différente des lois de la mécanique quantiquemécanique quantique de Heisenberg/Schrödinger, mieux adaptée aux calculs en théorie quantique des champs.

Richard Feynman, grand théoricien. © Tom Harvey
- D : Les confirmations expérimentales : les courants neutrescourants neutres et les bosons W

Courants neutres (chambre à bulles Gargamelle 1973). © DR
Le début des années 1970 voit la mise en évidence des courants neutres, c'est-à-dire l'existence de processus d'interaction faible liés à l'échange de Z0 et la découverte du quark charméquark charmé.
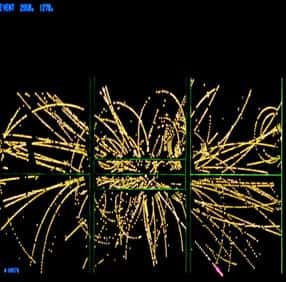
Découverte du boson W (CERN 1982). © CERN
Le modèle électrofaible et les théories de jauge acquièrent subitement une grande crédibilité et le couronnement aura lieu au début des années 80 avec la mise en évidence directe au CERNCERN des bosons W et Z.
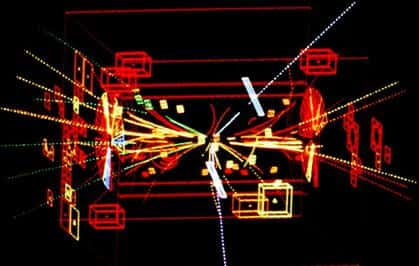
Désintégration de Z0 (expérience UA2, CERN). © CERN