Un trou noir et du rayonnement Hawking dans une fibre optique ?

En cherchant à prouver que l'on ne pouvait associer une entropie à un trou noir comme le proposait Jacob Bekenstein, Stephen HawkingStephen Hawking a fait sa fameuse découverte qui l'a rendu mondialement célèbre. Bekenstein avait en fait raison et, lorsque l'on applique la théorie des champs quantiques en espace-temps courbes à un trou noir, on trouve que ce trou noir doit rayonner comme un corps noir avec une température inversement proportionnelle à sa masse.

Malheureusement, cette température est bien en dessous de celle du rayonnement fossile dans le cas des trous noirs stellairestrous noirs stellaires, sans parler des trous noirs galactiques qui, au lieu de peser parfois la masse du SoleilSoleil comme les précédents, sont des millions à des milliards de fois plus lourds. Ainsi, non seulement le rayonnement de ces trous noirs est incroyablement faible, mais leur température étant plus basse que celle du rayonnement de fond diffus étudié finement par WMap, ils absorbent du rayonnement (celui du fond diffusdiffus) plutôt que d'en émettre !

Sous réserve bien-sûr que le rayonnement Hawking existe... Or, même s'il semble inévitable lorsque l'on cherche à rendre compatible la relativité généralerelativité générale, la thermodynamiquethermodynamique et la mécanique quantiquemécanique quantique, bien des zones d'ombres existent dans la dérivation théorique de celui-ci.

De même que les chercheurs peuvent simuler le comportement hydrodynamique des écoulements d'airair autour d'une maquette, ou la génération du champ magnétique de la Terre en laboratoire avec l’expérience VKS, il serait du plus haut intérêt de pouvoir simuler un trou noir par un phénomène physiquephysique facile à observer en laboratoire et reposant sur des équationséquations mathématiques analogues à celles décrivant un trou noir et le rayonnement Hawking.

Construire l'analogue d'un trou noir

Cette stratégie a été proposée il y a longtemps déjà par William Unruh qui, en 1981, démontrait qu'un écoulement supersonique pouvait en théorie reproduire l'analogue de l'horizon d'un trou noir et qu'une sorte de rayonnement Hawking en découlerait sous forme de quanta d'ondes sonoresondes sonores.

Pour se faire une idée de cette situation, rappelons qu'un trou noir n'est pas défini par l'existence d'une singularité mais par celle d'un horizon entourant une région de l'espace et l'isolant complètement de toute communication vers l'extérieur (un signal quittant cette région devrait dépasser la vitesse de la lumièrevitesse de la lumière).

Dans un écoulement d'air supersonique dans une tuyèretuyère, il peut exister une région du fluide de laquelle aucune onde sonore ne peut sortir, précisément à cause de la vitesse supersonique des écoulements. En considérant la vitesse du sonvitesse du son comme un analogue de la vitesse de la lumière, on obtient des conditions qui ressemblent à celles d'un trou noir.

On peut appliquer à l'équation du son les règles de la mécanique quantique, tout comme à l'équation de la lumière qui lui ressemble beaucoup. Il apparaît alors des quanta d'énergieénergie sonique analogues aux quanta de lumière que sont les photonsphotons. Comme il s'agit ici de son, on parlera tout naturellement de phononsphonons et, au lieu d'avoir un trou noir, on aura un trou muet (on parle aussi de trou noir acoustique), susceptible d'émettre un rayonnement sonique de corps noir.

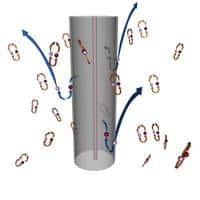
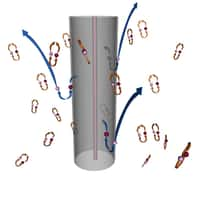
Figure 1. Représentation à deux dimensions d'un horizon (zone grise) évoluant au cours du temps du bas vers le haut selon un axe vertical. Des paires de particules apparaissent et produisent un rayonnement Hawking. © University of St Andrews

Tout se passe alors bien comme pour un trou noir et si l'on trace un diagramme d'espace-tempsdiagramme d'espace-temps, comme celui de la figure 1, le trou muet peut se voir comme une zone entourée d'un horizon (région grise) avec des paires de phonons-antiphonons apparaissant et disparaissant par fluctuations tout autour de l'horizon.

Un des phonons se dirigera vers l'horizon et, pénétrant à l'intérieur du trou sourd, il ne pourra plus en sortir ; l'autre quittera alors le voisinage de l'horizon pour être éventuellement absorbé par un capteurcapteur au loin.

D'autres analogiesanalogies hydrodynamiques sont éclairantes et valent la peine d'être mentionnées. La plus célèbre est celle de la cascade peuplée de poissonspoissons pouvant se déplacer avec une vitesse maximale c (elle est représentée sur la figure 2).

Si l'on considère la vitesse v de l'écoulement de l'eau, celle-ci augmente au fur et à mesure que l'on se rapproche de la cascade, qui peut être vue comme la singularité au sein de la solution classique de Schwarzschild décrivant un trou noir. Lorsque la vitesse v dépasse la vitesse maximale c des poissons, peu avant d'arriver à la cascade, on obtient un horizon de non retour pour les poissons au-delà duquel ils ne peuvent plus s'échapper et finiront inévitablement par tomber dans la cascade.

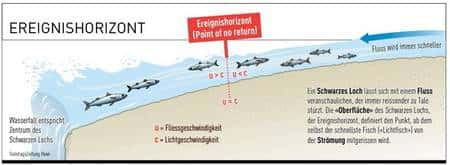
Figure 2. L'horizon de non-retour © SonntagsZeitung

Un trou blanc dans un évier

De même qu'il existe des trous noirs, il existe des trous blancs avec une frontière impénétrable de l'extérieur pour des particules. Un trou blanc émettra donc sans cesse de la matièrematière sans jamais en absorber et repoussera toute particule cherchant à y pénétrer.

On peut réaliser facilement un trou blanc chez soi avec un jet d'eau tombant dans un évierévier. La vitesse de l'écoulement de l'eau sera plus grande que celles d'ondes perturbant cet écoulement à l'intérieur d'une zone circulaire. Brutalement, sur l'analogue d'un horizon, les vitesses de ces ondes devenant plus importantes que celle de l'eau, les ondes seront clairement visibles, comme on peut le constater sur la figure 3.

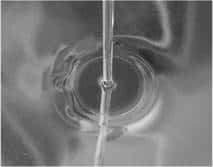
Figure 3. Un trou blanc peut se simuler chez soi dans un évier. Au voisinage du jet, tout est calme, mais passé une zone circulaire, l'horizon du "trou blanc", tout change. © University of St Andrews

En fait, la réalisation d'un trou noir acoustique et l'observation d'un rayonnement Hawking analogue avec celui-ci sont très difficiles en pratique. Toutefois, on a vu que les caractéristiques liées aux trous noirs sont modélisables par des fluides, comme John Wheeler l'avait fort bien compris. En effet, les équations non-linéaires de la mécanique des fluides donnent lieu à des phénomènes analogues à ceux de la géométrie de l’espace-temps gouvernés eux aussi par des équations non linéaires, celles d'EinsteinEinstein.

Or, comme on l'a vu récemment avec le phénomène des vagues scélérates, on peut simuler de l'hydrodynamique non linéaire avec de l'optique non linéaire dans des fibres optiquesfibres optiques. C'est pourquoi un groupe de chercheurs travaillant à l'université St Andrews a décidé d'étudier la question de la réalisation d'un trou noir optique analogue d'un trou noir dans une fibre optique.

L'équipe de Ulf Leonhardt s'est attelée au problème, et lui et ses collègues ont effectivement prouvé que cela pouvait se faire ; ils l'ont même réalisé !

Figure 4. L'équipe de l'Experimental and Theoretical Quantum Optics groups de l'université St Andrews travaillant sur les analogues otiques des trous noirs et du rayonnement Hawking. De gauche à droite, Ulf Leonhardt, Scott Robertson, Christopher E. Kuklewicz, Steve Hill, Friedrich König. © Experimental and Theoretical Quantum Optics groups de l'université St Andrews

Et dans une fibre optique ?

L'idée est simple : en envoyant un certain type d'impulsion laserlaser dans une fibre optique, celle-ci modifie tout autour d'elle l'indice de la fibre optique. Or cet indice est fonction de la vitesse limite à laquelle une onde lumineuse de fréquencefréquence donnée peut se propager. Cette modification d'indice se déplace avec l'impulsion lumineuse dans la fibre et cesse lorsque l'impulsion n'occupe plus une certaine région.

Si l'on envoie une seconde impulsion mais différente de la première, sa vitesse sera plus importante ou plus faible dans la fibre que la nouvelle vitesse de propagation d'une onde lumineuse de fréquence donnée au voisinage de la première impulsion. La première impulsion crée donc un horizon analogue aux exemples de trou sourd, cascade et jet dans un évier. Elle détermine autour d'elle une zone limite pour la propagation des autres ondes lumineuses, qu'elle transporte avec elle dans la fibre.

De sorte qu'en mesurant ce qui se passe pour les photons de la seconde impulsion, on trouve, comme les chercheurs l'ont observé, soit qu'ils traversent l'horizon et sont absorbés sans jamais en ressortir, soit qu'ils sont toujours réfléchis par l'horizon. Dans le premier cas, on est en présence d'un trou noir optique, et, dans le second, d'un trou blanc optique.

Figure 5. La fibre optique dans laquelle circule une impulsion laser. © University of St Andrews

Des expériences potentiellement instructives

Après cette première étape, reste à observer l'analogue de l'effet Hawking. Les chercheurs sont particulièrement intéressés par ce qui se passera pour de très courtes longueurs d'ondeslongueurs d'ondes, celles se rapprochant de la taille des atomesatomes composant la fibre par exemple.

En effet, certains pensent que l'on peut ainsi, non seulement tester les équations et les calculs de l'effet Hawking, mais également découvrir des effets subtils en liaison avec l'hypothèse d'une structure granulairegranulaire de l'espace-temps.

Plus généralement, il reste beaucoup de choses que nous ne comprenons pas dans le domaine de la gravitation quantiquegravitation quantique appliquée aux trous noirs. Ces simulations pourraient donc nous aider à y voir plus clair et à extraire expérimentalement des équations des éléments que nous ne voyons pas encore sur le plan théorique.