au sommaire
À partir d'une image simple, nous allons découvrir ce qu'est la dimension fractale, comment elle permet de quantifier la notion d'autosimilarité, et son caractère non intuitif. Par exemple, le fait que la longueur de la côte de Bretagne est potentiellement infinie.

Avant de nous aventurer à donner une définition théorique, le plus simple est de donner un exemple classique de fractale, la courbe de von Koch, dans sa variante appelée habituellement « flocon de neige de von Koch ». Cette courbe a été publiée en 1904 et le titre de l'article mérite d'être cité : « Sur une courbe continue sans tangente, obtenue par une constructionconstruction géométrique élémentaire ».
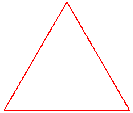
Cette « courbe » s'obtient en appliquant à chaque côté d'un triangle équilatéral une transformation simple : on remplace le 1/3 central de chaque côté par deux segments ayant la même longueur que celle qui a été prélevée et on recommence la même opération sur chaque côté de la figure obtenue. À la première itération (« Action de répéter, de faire de nouveau », Petit Larousse), on obtient une image proche d'une étoile de David, puis au fur et à mesure des itérations successives, le résultat mime plus ou moins un flocon de neige. Remarque capitale, à quelque grossissement qu'on examine la « courbe », on observera les mêmes détails... pour autant que le nombre d'itérations soit infini (ou, au moins, assez important).
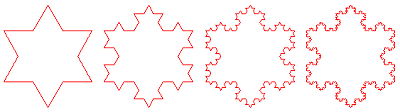
Remarquons au passage qu'il est matériellement impossible de dessiner exactement une fractale puisqu'il faudrait poursuivre les itérations à l'infini. En pratique, on s'arrête quand les plus petits détails sont inférieurs à la résolutionrésolution de l'écran.
Ce type de courbe présente une particularité bien curieuse. La première intuition conduit à penser que le périmètre de cette figure tend vers une valeur limite finie, puisqu'on ajoute des détails de plus en plus petits au fur et à mesure des itérations successives. En réalité, à la première itération la longueur L de chaque côté est remplacée par 4 segments de longueur L/3 ; à la deuxième elle devient 16 L/9... À chaque itération la longueur est donc multipliée par 4/3, ce qui signifie que (contrairement à l'intuition première) la longueur d'une courbe de Koch tend vers l'infini pour un nombre d'itérations infini (série géométrique de raison 4/3)). Et pourtant cette courbe ne déborde à aucun moment des limites constituées à l'extérieur par le cercle circonscrit au triangle initial, et à l'intérieur par le cercle inscrit dans ce triangle ! En d'autres termes une surface de dimension finie est limitée par une frontière de longueur infinie.
Question : sauriez-vous démontrer que cette surface tend vers
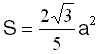
a étant la longueur du côté du triangle initial ?
Notion de dimension fractale
Une autre propriété encore moins intuitive est relative à la dimension géométrique des objets fractals (attention, ne confondez pas dimension et longueur !). Nous savons tous qu'un point est une figure de dimension 0 ; qu'une ligne droite est un objet de dimension 1 ; qu'une surface plane est un objet de dimension 2 ; qu'un volume est de dimension 3... Ceci est la dimension euclidienne ou topologique (en réalité ces deux termes ne sont pas strictement synonymes). Qu'en est-il d'un objet fractal ? Il existe plusieurs méthodes mathématiques pour exprimer la dimension d'un objet.
On peut tenter une approche simplifiée. Supposons qu'on veuille mesurer la limite (supposée droite) entre deux terrains, que cette longueur soit de 10 m et qu'on dispose d'une règle de 1 m. Il est évident qu'on doit l'appliquer 10 fois le long de la limite pour faire la mesure. Si la règle fait 0,5 m on devra la reporter 20 fois. Autrement dit, si l'on divise par n la longueur de la règle, on doit multiplier par n le nombre de fois où on la reporte, ce qui donne un rapport de n/n=1.
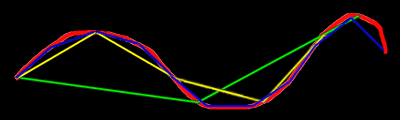
Si la longueur à mesurer est une courbe on comprend qu'en utilisant une règle droite reportée n fois de la même manière on n'aura qu'une valeur approximative, notablement sous-évaluée. Plus la règle sera courte, plus l'opération sera fastidieuse, mais plus le résultat sera précis. Pour une règle suffisamment (infiniment) petite, si je divise par n sa longueur, je multiplie encore par n le nombre de fois où je l'applique le long de la ligne et j'obtiendrai la longueur exacte de la courbe. Ceci donne toujours un rapport de n/n, soit 1 (c'est vrai aussi si j'écris ln n/ln n, remarque qui va nous servir bientôt). On voit clairement dans l'image ci-dessous qu'on se rapproche de plus en plus de la longueur réelle de la courbe rouge quand on prend la règle verte, la jaune et enfin la bleue.
Imaginons maintenant que je veuille paver une surface carrée de côté L. Si j'utilise un carreau unité de côté l = L/2 il faudra 4 de ces carreaux pour paver le carré initial. S'il a un côté de longueur l = L/4, il en faudra 16, etc. Si l'on divise le côté par un facteur n, on multiplie le nombre de carreaux par n2.
On ne peut pas utiliser dans ce cas le rapport n2/n pour mesurer la dimension d'une surface (on sait depuis EuclideEuclide qu'elle est égale à 2) car 4/2 = 2, mais 16/4 = 4, etc.
En revanche log n2/log n = 2 dans tous les cas. La même démarche s'applique pour les volumes où l'on aura log n3/log n = 3.
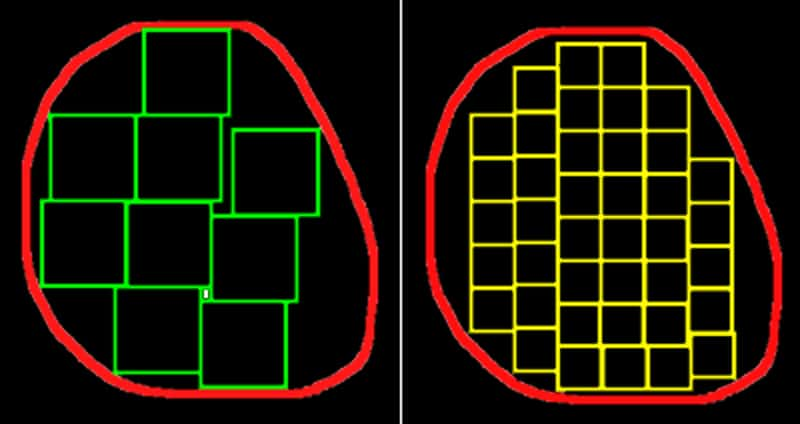
Prenons maintenant une surface quelconque, un carré unité quelconque et divisons-le successivement en utilisant un facteur quelconque n. Si la taille du carré n'est pas négligeable on ne peut pas paver de façon satisfaisante la surface et on va en sous-estimer la valeur. Soit N le nombre de carrés inclus dans la surface. Plus le carré est petit, plus le pavage est satisfaisant. Il est évident que la surface estimée sera d'autant plus proche de la surface réelle que le carré unité sera petit. Là encore on peut démontrer que log N/log n tend vers 2 si N tend vers l'infini. De même pour les volumes log N/log n tend vers 3 si N tend vers l'infini.
Pourquoi tant de complications puisque le résultat donne la valeur de la dimension euclidienne (ou topologique) bien connue ? C'est parce que, si c'est vrai pour les objets de la géométrie classique, ce n'est pas vrai dans d'autres cas.
Sans entrer dans les détails, on peut penser qu'un objet bizarre comme la courbe de Koch, qui a une longueur infinie tout en n'emplissant qu'une région très limitée du plan, doit avoir des propriétés très particulières. L'image ci-dessous montre en effet clairement que chaque fois qu'on réduit d'un facteur 3 la longueur de la règle, on multiplie par 4 le nombre de fois où l'on doit l'appliquer le long de la figure. Ceci démontre que sa dimension fractale est égale à ln 4/ln 3=1,26... Presque tous les objets fractals ont des dimensions non entières mais ce n'est pas obligatoire, contrairement à certaines définitions erronées qu'on peut lire.

Ceci est encore moins intuitif qu'une longueur infinie, mais nous amène à une définition à peu près correcte des fractales : les fractales sont des objets dont la dimension fractale est strictement supérieure à la dimension topologique.
Cette dimension est habituellement assimilée à la dimension de Hausdorff-Besicovitch. En fait, c'est faux et c'est vrai à la fois. Faux parce que l'expression générale de la dimension de Hausdorff-Besicovitch est très abstraite (elle est d'ailleurs souvent trop difficile à calculer pour être utilisée). Vrai parce que dans les fractales linéaires simples telles que la courbe de von Koch, les dimensions fractales et de Hausdorff-Besicovitch sont égales.
Si j'ai bien compris les explications de Mandelbrot dans l'appendice mathématique de son livre Les objets fractals, la dimension fractale semble être la dimension de recouvrement de Pontrjagin et Schnirelman : soit un objet situé dans un espace à n dimensions qu'on recouvre par le plus petit nombre N possible de « boules » de rayon r. Sa dimension de recouvrement est log N/log (1/r) quand r tend vers 0 (j'ai légèrement modifié la formule pour éviter un rô dont l'affichage dépend des jeux de caractères disponibles).
Il y a d'ailleurs d'autres approches de la notion de dimension qui ne sont pas toutes équivalentes et les travaux de Kolmogorov et Tihomirov relient la dimension de recouvrement à la notion d'entropie. Pour d'autres précisions, voir ici.
La côte de la Bretagne considérée comme une fractale
Le cas du flocon de von Koch nous conduit directement à une question abordée par Mandelbrot et qui a beaucoup contribué à la popularité des fractales : quelle est la longueur de la côte de la Bretagne ? En fait, le premier à avoir abordé cette question et à y avoir répondu correctement est Jean Perrin, dans une préface prémonitoire de son livre Les atomes, publié en 1913, texte auquel Mandelbrot rend un hommage appuyé dans Les objets fractals. Un extrait important du texte de Jean Perrin peut être consulté dans le PDF suivant : ici (pages 15 « Nous savons tous... » à 19 « ... le contour délicat et compliqué »).
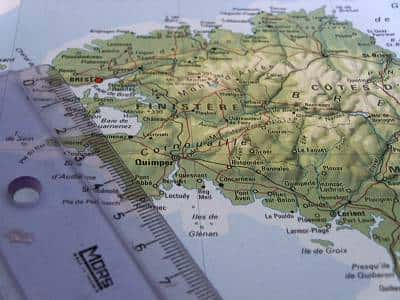
Remarquons que cette côte présente de très nombreuses circonvolutionscirconvolutions avec quelques grands golfes qui contiennent des golfes plus petits et des criques de toutes tailles, ainsi que des promontoires plus ou moins découpés. Sur le terrain nous observerons en outre des détails de plus petite taille qui ne peuvent pas être représentés sur la carte et qui sont dus aux irrégularités des rochers. Imaginons l'ogre du conte parcourant cette côte avec des bottes de 7 lieues. En comptant le nombre d'enjambées (n), il trouvera une longueur approchée pour cette côte (soit n fois 7 lieues). S'il enlève les bottes de 7 lieues pour faire le même chemin à pied, il trouvera une longueur plus importante. Imaginons le même voyage fait par le Petit Poucet (à pied), par un chienchien ou par une fourmifourmi : chacun trouvera une longueur plus grande et, chose importante, ces valeurs approchées ne convergent pas vers une longueur finie qu'on pourrait extrapoler à partir des résultats donnés par chacun. Au contraire, tout comme le flocon de von Koch, la longueur de la côte de la Bretagne est, en toute rigueur, infinie.
Quelle est la contribution de Mandelbrot au problème de la longueur des côtes ? Dans l'article « How long is the coast of Britain ? Statistical self-similarity and fractional dimension » (Sciences, 155, 636-638 ; 1968), l'auteur part des résultats d'un article peu connu de Richardson où ce dernier montre que la longueur d'une côte est fonction d'une puissance α du pas (au sens de l'explication ci-dessus). Là où ce dernier ne voyait dans α qu'un exposant empirique de sa formule, Mandelbrot interprète 1+α comme une dimension (au sens de Hausdorff et Besicovitch) et montre la nature fractale (le terme n'existait pas encore) des côtes. Ce travail semble avoir été à l'origine des recherches de Mandelbrot et de ses continuateurs sur l'utilisation des fractales pour obtenir des images de synthèse de paysages. En effet, un raisonnement du même type peut être appliqué au relief, c'est-à-dire en passant de la dimension euclidienne 2 à la dimension 3.
Autosimilarité
Reprenons une phrase écrite plus haut à propos de la courbe de von Koch : « Remarque capitale, à quelque grossissement qu'on examine la "courbe" on observera les mêmes détails ». Ceci est une propriété importante de toute structure fractale désignée par les termes « autosimilarité », « homothétie interne » ou encore « invariance d'échelle ». Cette propriété s'explique par le fait que toute image fractale est engendrée par un processus d'itération théoriquement infini. Dans le cas de la courbe de von Koch les choses sont très simples puisque les détails sont rigoureusement identiques quelle que soit l'échelle. C'est pourquoi, quand on regarde une portion de cette figure il est impossible de dire si on la regarde à l'échelle 1, ou si l'on a fait un zoom de 10 fois, 100 fois, ou 1 million de fois.
Mais cette stricte identité n'est qu'un cas particulier. Dans de nombreuses fractales obtenues à partir de fonctions mathématiques, les détails sont simplement similaires sans être strictement identiques. Il en est de même pour les structures fractales observées dans les objets naturels : les différents golfes et les criques de la côte de Bretagne n'ont pas exactement le même dessin ; il n'empêche que cette côte a indiscutablement une structure fractale dont on peut calculer la dimension. En outre, les structures fractales naturelles ne sont pas fractales à l'infini : l'autosimilarité s'arrête en général à un moment (si en explorant la côte on tombe sur une jolie plage de sablesable fin bien régulière, il est évident qu'elle n'est pas fractale).
Les images fractales théoriques ont donc une propriété que ne montre aucune autre figure géométrique ou aucune courbe mathématique : on peut zoomer dedans à l'infini, on observera toujours de nouveaux détails. C'est cet aspect particulier de la notion d'infini qui rend les fractales si fascinantes et qui a contribué à leur popularité (au point même que certains en ont tiré des élucubrations mystico-philosophiques). Cette propriété est largement exploitée par les créateurs d'images fractales calculées par ordinateurordinateur. Songez qu'une image de 1.600 x 900 pixelspixels comporte 1.440.000 points calculés individuellement et faisant l'objet d'au moins 100 à 200 itérations chacun (et souvent bien plus) pour avoir une image assez précise : vous imaginez combien la puissance des ordinateurs modernes est utile. Il n'était pas rare il y a 15 ou 20 ans que certaines images aient nécessité plusieurs jours de calcul.

































