au sommaire
De nombreuses opérations géométriques ou mathématiques peuvent engendrer des fractales. Cette page rassemble divers exemples partant des plus simples pour aller vers des méthodes plus complexes. Au passage nous verrons comment il est possible de créer simplement des images de plantes.

Constructions géométriques simples et résultats surprenants
Avec la courbe de von Koch, la poussière de Cantor, la courbe du dragon (voir page 4 de ce dossier intitulée « Fractales et chaos »), nous venons de voir un premier ensemble de fractales construites simplement par l'itération d'une opération géométrique simple. Cela ne met en œuvre aucun concept compliqué et pourtant on aboutit à des figures dont les propriétés auraient paru impensables à EuclideEuclide puisque leur dimension n'est pas 2. En voici quelques autres exemples, avec un faible nombre d'itérations pour garder leur lisibilité :
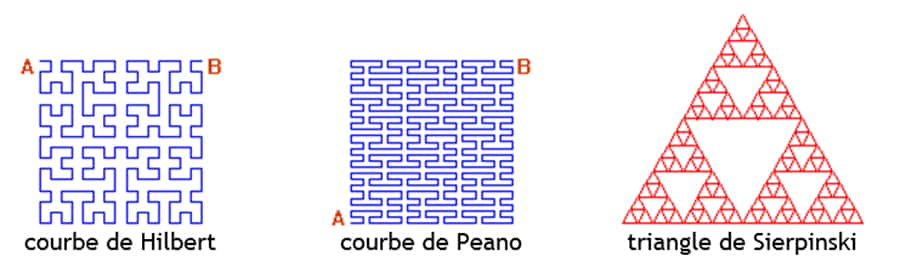
Avec un nombre d'itérations infini, les courbes de Hilbert et de Peano ont pour caractéristique de passer par tous les points du plan. Leur dimension fractale est donc 2, alors que leur dimension euclidienne est 1. En outre, ce sont des courbes sans tangentes. Le triangle de Sierpiński a une dimension fractale égale à log 3/log 2, soit approximativement 1,585.
L-systèmes
Les Lindenmayer-systèmes (L-systèmes) n'ont pas été inventés pour créer des fractales mais pour modéliser la croissance et les interactions cellulaires. Un L-système est une grammaire formelle dont les règles définissent la procédure pour transformer par itération une chaîne de caractères de départ en une autre chaîne. Les transformations sont basées sur des règles qui spécifient comment des caractères ou parties de la chaîne de caractères sont remplacés par d'autres. Si on applique cet ensemble de règles de façon récursive à une chaîne de caractère, une nouvelle chaîne ayant une structure fractale peut être créée.
Fondamentalement, chaque caractère peut être un symbole ayant n'importe quelle signification conventionnelle, mais on a utilisé très tôt les L-systèmes pour dessiner des figures complexes, chaque caractère étant interprété comme une commande graphique.
Les conventions peuvent être choisies librement par chaque programme utilisant les L-systèmes. L'exemple suivant est extrait du manuel du célèbre programme de fractales Fractint. Il utilise donc la syntaxe de ce programme (remarque : tout ce qui suit un point-virgule est un simple commentaire).
Dragon { nom du l-système, "{" indique le début de la procédureAngle 8 ; spécifie que l'incrémentincrément de l'angle est 45° (360/8)
Axiom FX ; chaîne de caractère initiale
F= ; première règle: effacer 'F'
y=+FX--FY+ ; changer 'y' en "+fx--fy+"
x=-FX++FY- ; même transformation sur 'x'
}
; le "}" marque la fin de la procédureLa courbe du dragon montrée précédemment a été obtenue en indiquant au programme d'appliquer cette procédure 10 fois de façon récursive.
Pour interpréter cet exemple, voici les commandes standard utilisées :
F tracer un trait vers l'avant+ augmenter l'angle de la valeur fixée
- diminuer l'angle
Et voici comment a été dessiné le triangle de Sierpinski :
Sierpinski { axiom F+F+F
f=F[+F]F
angle 3 }
Enfin les L-systèmes ont été largement utilisés pour modéliser la structure des végétaux. En voici un exemple utilisant un programme un peu plus élaboré.

IFS (Iterated Function System)
C'est un type de fractales assez original qui a été introduit par Michael Barnsley. Ce type de fractales n'est pas facile à expliquer à des non-mathématiciensmathématiciens. Leur structure est décrite par un ensemble de fonctions affines qui calculent les transformations appliquées à chaque point par homothétie, translation et rotation. Chaque transformation utilise deux fonctions pour calculer les nouvelles valeurs x1 et y1 des coordonnées x et x de chaque point :
ax+by+e=x1cx+dy+f=y1
Enfin, une probabilité comprise entre 0 et 1 est associée à chaque transformation (le total de toutes les probabilités devant être 1). Ces images sont donc construites par un processus aléatoire : on voit apparaître sur l'écran des points de plus en plus nombreux qui dessinent une forme floue, puis de plus en plus précise. En général le programme permet de fixer le critère d'arrêt du calcul. Plus le temps choisi est long, plus les images sont précises. En voici deux exemples :
Le triangle (ou tamis) de Sierpinski
sierpinski { 0.5 0 0 0.5 0 0 0.333
0.5 0 0 0.5 1 0 0.333
0.5 0 0 0.5 0.5 0.8660254 0.334 }

Dans cette syntaxe, les quatre premiers termes sont les coefficients a, b, c, d des équations, les deux suivants sont les termes constants e et f. Le terme 0.8660254 est le sinus de 60°. Enfin, la dernière probabilité a été arrondie à 0.334 pour que le total soit égal à 1.
Enfin, voici la célèbre fougèrefougère de Barnsley :
fougère { 0 0 0 0.16 0 0 0.01
0.85 0.04 -0.04 0.85 0 1.6 0.85
0.2 -0.26 0.23 0.22 0 1.6 0.07
-0.15 0.28 0.26 0.24 0 0.44 0.07 }

Les IFSIFS ont servi à développer une méthode de compression des images efficace mais qui n'a pas obtenu une grande diffusion et seuls des programmes spécialisés savent afficher ces images, contrairement au format JPeg bien connu.
Une technique IFS en 3D est utilisée par un programme étonnant, Xenodream, qui permet de créer de manière interactive des images d'objets de toutes sortes, des plus réalistes aux plus abstraits, et de leur appliquer des effets de texturetexture et d'éclairage extraordinairement variés. Il est souvent impossible d'imaginer, en regardant l'image achevée, qu'elle a été créée par un procédé fractal.
Fractales « flammes »
En fait ces fractales sont connues sous leur nom anglais (flame fractals). Il s'agit d'une combinaison d'attracteurs étranges produits par la méthode IFS, auxquels sont appliqués un ensemble de transformations très complexes. Comme toutes les fractales de type IFS, elles se construisent progressivement par accumulation de points apparaissant de façon semi-aléatoire. En utilisant un nombre d'itérations élevé et une palette de couleurs très progressive on peut obtenir des images très délicates. Au contraire, l'image montrée ici a été arrêtée après un nombre d'itérations modéré pour montrer sa constructionconstruction point par point ; elle n'a donc aucune prétention esthétique.

































