au sommaire
Les photons ne sont plus des particules libres mais sont prisonniers d'un plasma opaque quand l'Univers est plus jeune que 380.000 ans après le Big BangBig Bang. Les premiers photons que l'on peut mesurer sur terre sont issus de la surface de dernière diffusion, lorsqu'ils peuvent enfin s'échapper du plasma de particules.

L'expansion de l'Univers du Big Bang à nos jours. © Andrea Danti, Shutterstock
Ces photons ont une énergie qui est distribuée comme celle d'un corps noir, c'est-à-dire que le spectrespectre des photons est thermique, de température environ 3000K. Avec l'expansion de l'Univers, la température du rayonnement a chuté et nous recevons des photons thermiques de température aux environs de 2,7 K. On appelle rayonnement de fond cosmologique ce flux de photons primordiaux. Sa température est extraordinairement uniforme sur tout le ciel. Elle ne varie que d'une fraction de 10-5 K. Ces petites variations de la température du rayonnement de fond sont une des découvertes scientifiques majeures des vingt dernières années. L'analyse de l'origine de cette petite fraction conduit à de nombreuses avancées théoriques que nous allons décrire.
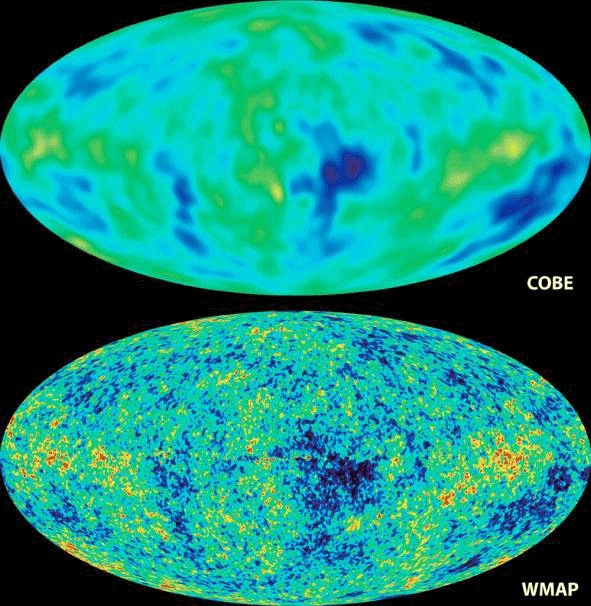
Une carte de la température du rayonnement de fond cosmologique comme mesurée en 1992 par le satellite COBE puis à partir des années 2000 par le satellite WMAP. La température sur la voûte céleste est essentiellement constante à part de petites fluctuations de l’ordre d’un cent millième. Crédit : Nasa.
Revenons d'abord sur la quasi-uniformité du rayonnement de fond. Cette isotropieisotropie est une énigme car elle semble violer la causalité. En effet, les portions du ciel lors de la dernière diffusion qui sont éloignées de plus d'un degré ne peuvent avoir été en contact dans le passé de l'Univers. Comment peut-on alors expliquer une telle uniformité ? Quel processus physiquephysique a impliqué que des portions du ciel qui ne peuvent s'être échangé de signaux et d'information aient des températures quasi égales ?
Cette question voit sa réponse dans l'ère la plus ancienne à laquelle nous pouvons avoir accès. En effet, les fluctuations de température du rayonnement de fond dépendent de la physique qui aurait eu lieu juste après le Big Bang avant que la matièrematière ordinaire ne soit créée. A cette époque, l'Univers est essentiellement composé de ce que l'on appelle un champ scalaire , c'est-à-dire un bosonboson de spinspin nul. La dynamique du champ scalaire est décrite par son énergie potentielleénergie potentielle
. Le champ scalaire est essentiellement uniforme dans tout l'espace. Son comportement temporel est analogue à celui d'une boule roulant le long d'une pente (son énergie potentielle) et soumis à une force de frottement (due à l'expansion de l'Univers). Lorsque la pente est suffisamment douce, le champ scalaire que l'on baptise inflatoninflaton est pratiquement immobile. Son énergie potentielle est quasi constante. Ceci a pour effet d'engendrer une croissance exponentielle de la taille de l'univers, plus rapide que la lumièrelumière. Ainsi notre univers observable ne serait que le résultat de l'extraordinaire expansion inflationnaire d'une toute petite partie de l'Univers avant le début de l'inflation. Comme cette petite partie est uniforme initialement, ceci explique pourquoi la température du rayonnement de fond l'est aussi : nous n'observerions qu'un tout petit morceau de l'Univers dont la taille est devenue gigantesque après l'inflation.
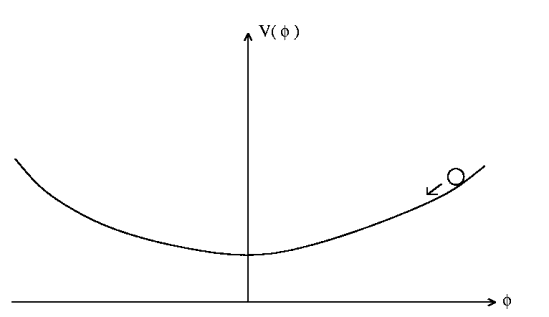
L’Univers pendant l’inflation est uniquement composé du champ d’inflation qui est uniforme spatialement mais dont la valeur varie dans le temps. Cette valeur suit la loi de la chute d’une boule le long d’un potentiel très peu pentu et soumise à de la friction. Pendant l’inflation, l’inflaton est quasi immobile. Son énergie potentielle est celle qui crée un accroissement exponentiel de la taille de l’Univers.
Ce mécanisme ne serait pas très prédictif si les fluctuations de la température du rayonnement de fond ne portaient en elles des informations cruciales sur la phase inflationnaire. Pour ce faire, on décompose les fluctuations de température sur la carte du ciel en harmoniques comme on le ferait pour le son d'un instrument de musique. Chaque harmonique l correspond à une variation de la fluctuation de température sur un angle de l'ordre de 1/l. Les grands l correspondent aux fluctuations sur de petits angles quant aux petits l ils sont associés aux fluctuations sur de grands angles. On trace alors le spectre des fluctuations en fonction de ces harmoniques. Ce spectre est fait de creux et de bosses, chacun nous renseignant sur la physique de l'univers primordiale. On apprend ainsi qu'à un très haut degré de précision, l'univers est spatialement plat. Il est aussi possible de remonter à certaines caractéristiques du potentiel de l'inflation. En fait, on peut ainsi mesurer les paramètres pertinents qui caractérisent la théorie effective décrivant l'inflation. En un sens, le rayonnement de fond cosmologique et sa description par l'inflation sont le succès ultime de l'approche de la dynamique de l'Univers par des théories effectives.
Quels sont ces paramètres auxquels l'expérience nous donne accès ? Ils sont de trois types et nécessitent l'introduction de deux paramètres fondamentaux. Le premier mesure la pente du potentiel d'inflation pendant l'inflation, le second
caractérise sa courbure. Le troisième ingrédient V0 n'est autre que la valeur du potentiel pendant la phase inflationnaire. Ainsi la physique du rayonnement de fond dépend des trois premiers termes du développement de Taylor du potentiel pendant la phase inflationnaire :
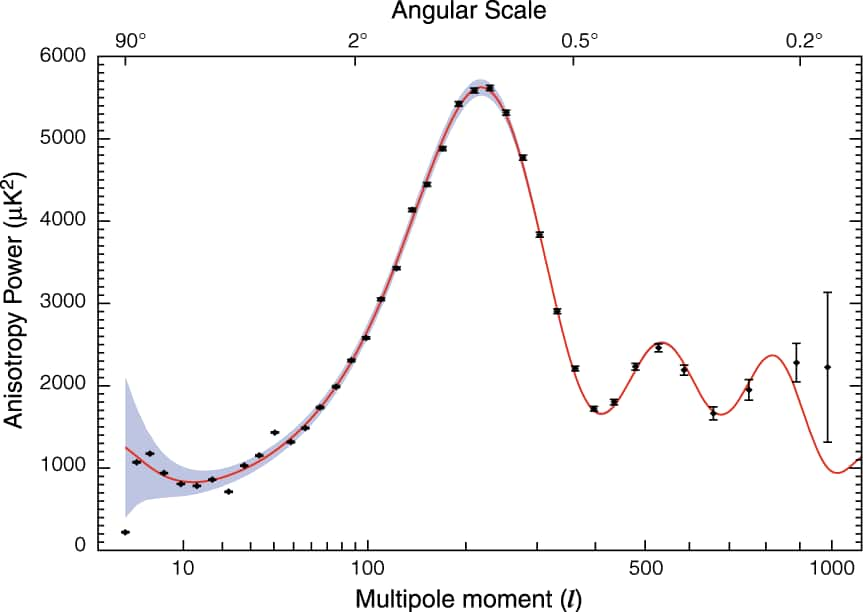
Le spectre des harmoniques des fluctuations du rayonnement de fond cosmologique. Ce spectre nous renseigne sur les caractéristiques de la phase inflationnaire. Crédit : Nasa.
Le spectre du rayonnement de fond cosmologique nous permet de connaitre la normalisation du potentiel :
et l'indice spectral qui caractérise le spectre des fluctuations issus de l'inflation:
Evidemment, ceci ne détermine que deux des trois paramètres. C'est pour cette raison que l'échelle de l'inflation n'est pas complètement déterminée.
Les fluctuations de la température du rayonnement de fond cosmologique ont une origine physique très précise. Lors de l'inflation, l'inflaton est quasi-immobile. Il existe cependant des fluctuations quantiques de sa valeur. Cette incertitude quantique sur la valeur de l'inflaton pendant l'inflation se retranscrit directement dans les fluctuations de température : ainsi un phénomène cosmologique comme la variation de température du rayonnement de fond sur le ciel a une origine quantique !
De même que l'inflaton peut fluctuer quantiquement, la métrique de l'espace-tempsespace-temps peut aussi fluctuer pendant l'inflation. Ces fluctuations quantiques donnent lieu à des ondes gravitationnellesondes gravitationnelles qui sont intensivement cherchées. Le rapport r des amplitudes des ondes gravitationnelles à la fluctuation de l'inflaton est simplement donné par :
Une détection des ondes gravitationnelles primordiales permettrait de caractériser complètement le potentiel de l'inflaton pendant l'inflation. Ce serait aussi une éclatante confirmation du caractère quantique des processus ayant lieu pendant l'inflation.
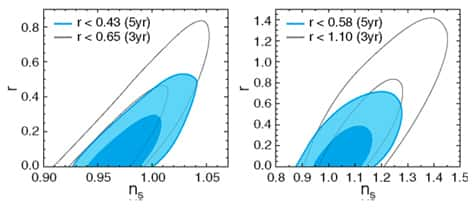
Contraintes expérimentales données par le satellite WMAP après 3 ans et 5 ans de fonctionnement.
L'inflation est le phénomène le plus ancien auquel nous avons accès par l'expérience. Bien sûr, rien n'exclut l'existence de phases antérieures à l'inflation. Comme nous l'avons vu, a partir d'énergies atteignant la massemasse de PlanckPlanck, il faut tenir en compte des effets quantiques de la gravitégravité. La constructionconstruction d'une théorie quantique de la gravité est une tache ardue. Il existe plusieurs candidats mais celui qui a les faveurs de nombreux physiciensphysiciens s'appelle la théorie des cordesthéorie des cordes. Celle-ci remplace la notion de particule ponctuelle par celle d'objets étendus, des cordes, dont la taille devrait être de l'ordre de l'échelle de Planck, c'est-à-dire 10-35 m. De plus ces cordes ne vivraient pas dans quatre dimensions mais dans dix, six d'entre elles seraient si petites qu'elles ne seraient pas observables directement. Pour être une théorie physique, elle doit être comparée avec l'expérience. Du fait de son existence dans une phase précédent l'inflation, la meilleure chance de tester la théorie des cordes est sans doute la cosmologiecosmologie. On peut ainsi imaginer que la théorie des cordes détermine le modèle d'inflation qui décrit la phase inflationnaire. Malheureusement, nous en sommes encore loin.
Une vue d’artiste des six dimensions supplémentaires de la théorie des cordes: ici une surface de Calabi-Yau est répétée périodiquement sur un réseau carré. Crédit : Jeff Bryant.