au sommaire
La stabilité des fusées
1. Les types de vol
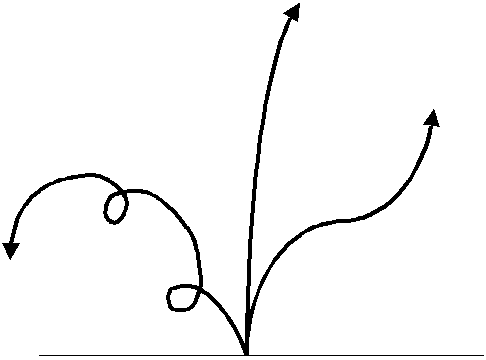
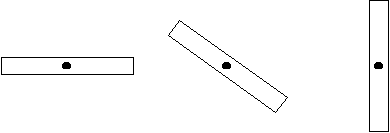
Si l'on fabrique et tire une fuséefusée miniature en disposant des ailettes "au hasard", sans se soucier de la stabilité de la fusée, on aboutira immanquablement à l'un des trois types de vol suivants : instable, stable ou surstable.
Le vol instable, malheureusement le plus fréquent si aucune démarche de calcul ou de vérification n'a été entreprise, peut être comparé à la trajectoire d'un ballon gonflable mais percé ou non bouché : il vole dans tous les sens ; la trajectoire est totalement imprévisible ; ça ne monte pas très haut. Pour le cas d'un ballon, c'est amusant. Pour une fusée miniature, c'est dangereux. A la fois pour la fusée qui risque de percuter le sol à pleine vitesse et d'être par conséquent détruite. Et aussi pour l'environnement, qui risque de recevoir la fusée... Dangereux et sans intérêt, à éviter par conséquent.
Le vol surstable est meilleur, sans être toutefois optimal. La fusée a trop de surface d'ailettes et ce sont ces dernières qui guident principalement le vol. D'où la répercussion de leurs défaut sur ceux du vol : ailette en biais, vol en biais ou ailettes en hélice, vol en hélice. Le vol est globalement rectiligne, mais l'altitude atteinte est réduite par les frottements dus à ces ailettes excessives. De plus, le vol n'est pas très gracieux. De nouveau, c'est à éviter.
Enfin, le vol stable est un vol rectiligne, régulier et qui permet à la fusée d'exploiter tout son potentiel pour atteindre l'altitude maximale.
Voici, schématiquement, à quoi ressemblent les différents types de vols :

Au centre, vol stable
A droite, vol surstable
Nous allons voir ci dessous comment obtenir un vol stable.
2. Centre de gravité et centre latéral de poussée
Nous allons maintenant pénétrer davantage dans les domaines physiques et mathématiques. Mais avant tout, il faut préciser que la méthode ci-dessous n'est pas le pur fruit d'une démarche mathématique. Il n'est en effet pas possible de poser en équations strictes et rigoureuses les phénomènes aérodynamiques auxquels nous nous intéressons. Une partie des équations que l'on trouvera ci-dessous sont des résultats mathématiques de théories physiques mais une autre partie est le résultat de l'expérimentation. La démarche est alors : on essaie, cela fonctionne (ou non) et on tente d'en déduire les formules qui permettront de répéter le résultat. En bref, la méthode ci-dessous est empirique, et par conséquent faillible. Le domaine d'application des formules n'apparaît pas intuitivement et il peut être nécessaire de recourir de nouveau à l'expérimentation pour en tester la validité dans des parties extrêmes de leur champ d'application. En plus clair, ces formules peuvent parfois (mais très rarement dans notre cas) se "tromper" !
Abordons maintenant deux notions fondamentales pour la suite de notre étude : le centre de gravitégravité et le centre latéral de poussée. Si le premier est bien connu et facile à déterminer, le second est plus difficile à appréhender, mentalement et physiquement.
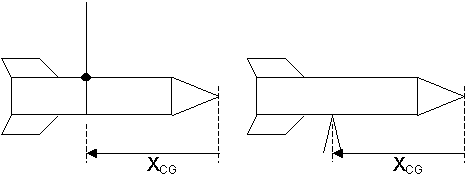
Le centre de gravité est le centre de répartition des massesmasses. Physiquement, si on tient un objet par ce point, l'objet en question est fixe et ce quelle que soit la position qu'on lui donne. Par exemple, si l'on considère un objet parallélépipédique constitué de matièrematière homogène (son centre de gravité est alors confondu avec son centre géométrique), cet objet, s'il est tenu en son centre de gravité, acceptera sans bouger toutes les positions :
Trois positions stables pour notre objet
Le centre latéral de poussée est, quant à lui, le point de la fusée où s'applique la résultante de toutes les forces aérodynamiques s'exerçant sur la fusée. En d'autres termes, chaque élément de la fusée va, lors du mouvementmouvement de la fusée, devenir le point d'appui de l'airair environnant et par conséquent recevoir de ce dernier une force aérodynamique qu'il transmettra à l'ensemble de la fusée. L'ensemble de ces forces (la résultante) crée donc un effort sur la poussée. Cet effort sera décomposé en deux parties, dont seule une nous intéressera : l'effort longitudinal et l'effort latéral :
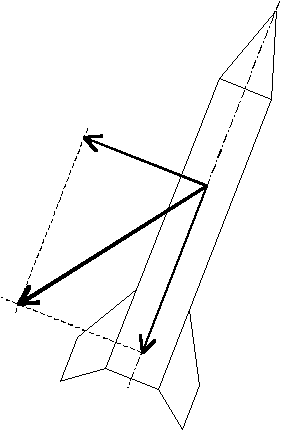
Parallèlement à la fusée : l'effort longitudinal
Perpendiculairement à la fusée : l'effort latéral
On ignorera l'effort longitudinal car, si la fusée est symétrique par rapport à son axe, il ne peut engendrer de déviation de la fusée et a pour seul effet de réduire l'altitude atteinte. C'est ce qu'on appelle communément le "frottement de l'air".
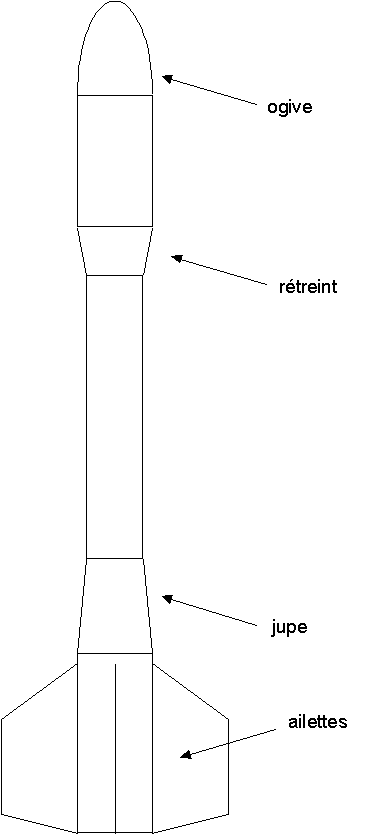
L'effort latéral dépendra, comme nous l'avons vu plus haut, de tous les éléments de la fusées : ogive, jupe (élargissement de diamètre du corps), rétreint (diminution du diamètre du corps), ailettes. Seul le corps de la fusée ne sera pas considéré (s'il est section constante et centrée sur l'axe principal de la fusée) car son effet s'annule par effet de symétrie.
3. La marge statique
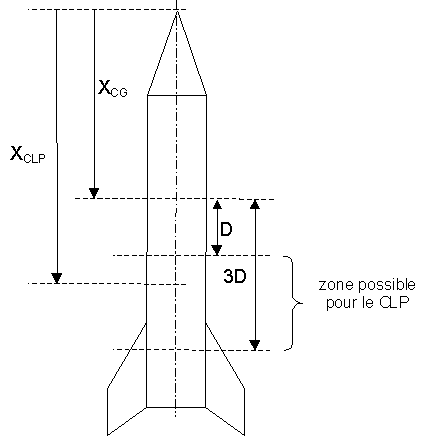
La marge statique est le point clé de la stabilité en vol des fusées. Elle est définie comme la distance séparant le centre de gravité et le centre latéral de poussée.
Une fusée sera stable si :
- Son centre de gravité est au dessus de son centre latéral de poussée,
- Sa marge statique est comprise entre 1 et 3 fois son diamètre moyen (2 fois idéalement).
En appelant D le diamètre moyen de la fusée, X_CG la distance séparant l'extrémité de l'ogive du centre de gravité et X_CLP la distance séparant l'extrémité de l'ogive du centre latéral de poussée, la condition de stabilité de la fusée s'écrit :
D CLP-XCG XCLP-XCG = 2D dans le cas idéal
4. Marge statique et type de vol
Maintenant que nous avons étudié la marge statique, nous pouvons faire le lien entre cette dernière et le type de vol :
- Si la marge statique est trop faible (inférieure à D, ou même négative), les forces aérodynamiques s'exercent trop près du centre de gravité de la fusée (là où s'exerce la poussée du moteur) ou au dessus et la moindre perturbation renverse la fusée et son vol devient chaotique : le vol est instable,
- Si la marge statique est trop importante (supérieure à 3D), les forces aérodynamiques ne risquent pas de renverser la fusée, mais, comme nous l'avons vu plus haut, elles sont si importantes qu'elles nuisent au bon vol de la fusée : le vol est surstable,
- Si la marge statique est conforme (de 1 à 3 fois le diamètre moyen), la fusée est équilibrée, les forces aérodynamiques sont suffisantes sans être excessives : le vol est stable.