S’inspirant de la légende du baromètre de Bohr, des physiciens français et leurs étudiants se sont penchés sur les méthodes possibles pour mesurer la hauteur d’un immeuble à l’aide d’un simple smartphone : pendule géant, ombre portée, vitesse du son, gravité… À leur grand regret, ils ont constaté que les plus simples sont aussi les plus fiables.
au sommaire
Vous connaissez peut-être la légende du baromètrebaromètre de Bohr ? Niels BohrNiels Bohr, alors étudiant, à qui l'on avait demandé de calculer la hauteur d’un immeuble avec un baromètre lors d'un examen de physique, avait répondu « Emmenez le baromètre en haut de l'immeuble, attachez-le au bout d'une corde et descendez-le jusque sur le sol. Remontez ensuite la corde et mesurez sa longueur. La longueur de la corde vous donne la hauteur de l'immeuble ». Il avait ensuite proposé toute une série de méthodes insolites pour parvenir à un résultat dont celle d'aller cogner à la porteporte du concierge et de lui dire : « Monsieur le concierge, j'ai ici un très beau baromètre. Si vous me donnez la hauteur de l'immeuble, il est à vous ».
Théorie et sens pratique
Bien que cette légende urbaine ne soit pas véridique, elle a inspiré Frédéric Bouquet et ses collègues du Laboratoire de Physique des Solides d'Orsay, pour un article intitulé 61 façons de mesurer la hauteur d'un immeuble avec un smartphone, et paru sur le serveurserveur de pré-publication arXiv. Le professeur, de l'université de Paris-Saclay, a demandé à ses étudiants de plancherplancher sur toutes les méthodes possibles pour répondre à cette question, d'évaluer la précision des mesures ainsi que l'écart entre le calcul théorique et la mesure réelle. Les étudiants devaient uniquement utiliser des objets du quotidien et un smartphone muni des capteurscapteurs internes (accéléromètre, gyroscopegyroscope, caméra, magnétomètre, GPSGPS, micro, etc.)).
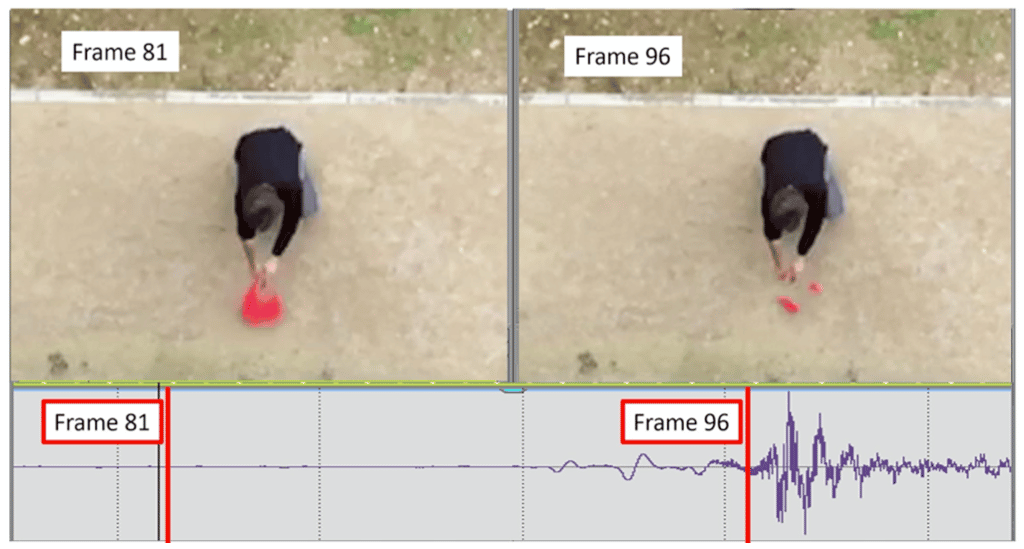
Les premières solutions envisagées consistent à faire chuter le téléphone depuis le haut de l'immeuble. En négligeant la friction de l'air, on peut en déduire que la hauteur est égale à 1/2 gtt2. Le temps de chute peut être estimé par différents moyens, par exemple en utilisant un enregistrement audio. « Dans ce cas, une méthode simple pour produire un son au début de la chute consiste à attacher le smartphone à un ballonballon et à l'éclater », écrivent les auteurs. Ces méthodes donnent une hauteur plutôt fiable, à 0,3 ou 1 mètre près.

Pendule géant et ombre portée
Une autre possibilité consiste à utiliser un pendule géant, en suspendant le smartphone à une corde de la hauteur de l'immeuble. Grâce à la formule H = g(T/2π)2, où T est la période, on obtient une estimation de la hauteur. La période T peut être elle-même évaluée par différents moyens (accéléromètreaccéléromètre du smartphone, gyroscope, analyse vidéo...). D'autres méthodes ont recours à la trigonométrietrigonométrie. La méthode n° 21 propose par exemple de mesurer la taille de l'ombre du bâtiment et de celle du smartphone, qui donne alors donne le rapport hauteur du bâtiment/dimension du smartphone. Autre possibilité (n° 23) : utiliser un time-lapsetime-lapse pour déterminer la taille minimale de l'ombre lors d'un jour d'équinoxeéquinoxe ou de solsticesolstice.
Physique ondulatoire
Il y a aussi les méthodes acoustiques, ou celles utilisant la physique ondulatoire. « Une configuration directe consiste à utiliser deux smartphones et un haut-parleur émettant un son continu pur, décrit l'article. Au début, ils se trouvent tous au bas du bâtiment, au pied d'un escalierescalier extérieur. Les deux smartphones enregistrent le son, l'un est laissé au sol, l'autre est lentement amené en haut en utilisant les escaliers extérieurs, tout en enregistrant le son continu. L'analyse des deux enregistrements audio montrera une augmentation de la différence de phase entre les deux smartphones, liée à la distance entre le smartphone du haut et le sol.
Une hauteur égale à zéro… à 3 millions de kilomètres près
Les chercheurs se sont également penchés sur des méthodes « qui ne fonctionnent que dans la théorie ». Par exemple, en supposant que la Terre est un dipôle magnétique parfait, l'utilisation du magnétomètre pour mesurer le champ magnétique en haut et en bas du bâtiment devrait permettre de déduire la hauteur H. Problème : « Un changement d'altitude de 15 m correspondrait à un changement de 0,0008 % du champ magnétiquechamp magnétique, en dessous de la résolutionrésolution standard des capteurs des smartphones ». En pratique, cela aboutit à une mesure divergeant de 40 % par rapport au modèle théorique, ce qui se traduit par une différence de « plusieurs centaines de kilomètres ».
La palme revient à la méthode Variation de la gravitégravité entre le sommet et le sol, déterminée par la dilatationdilatation du temps de la relativité généralerelativité générale, qui nous donne une hauteur H égale à 0 avec, toutefois, une marge d'erreur de 3 millions de kilomètres. Ce qui conduit les chercheurs à conclure, peut-être à regret, « qu'en moyenne, plus la méthode est simple, plus les résultats sont précis ». Une des techniques les plus fiables est ainsi de compter le nombre de marches d'escaliers avec l'accéléromètre et de multiplier par la hauteur de la marche.
De façon décevante, la méthode n° 61 n'a pu donner aucun résultat du tout. Elle est intitulée Appel téléphonique à l'architectearchitecte du bâtiment.
























