au sommaire

Sur les difficultés de servir un apéro au pays de Lilliput
Imaginez un peu un frigo Lilliputien réglé à 1 degré Celsius ! Dans le microscopique bac à glace, vous trouvez à peine moins de la moitié des alvéoles gelées et les autres liquides. Vous pensez que quelque chose ne va pas et avec votre thermomètrethermomètre, vous contrôlez un à un chaque glaçon.

Gulliver au pays des Lilliputiens (Jonathan Swift, 1723)
Non ! Ils sont bien à un degré ! Vous décidez de tout remettre dans le réfrigérateur et de pousser le thermostatthermostat a - 1 degré pour pouvoir servir de beaux glaçons à vos amis. Une heure plus tard c'est la déconvenue ! Il n'y a que quelques glaçons supplémentaires, la moitié du bac étant resté liquide. Pourtant l'ensemble est bien à -1 degré !
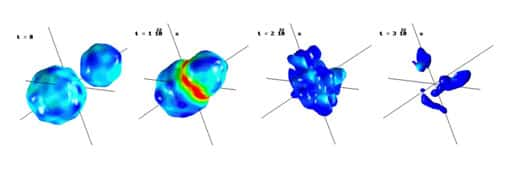
Alors que vous étudiez ces drôles de glaçons, le soleil sort derrière une molécule de nylon qui vous servait de parasol. Ses rayons réchauffant ces glaçons qui ne contiennent que quelques dizaines de molécules, vous observez que leur température augmente : 0, 1, 2 puis 3 degrés défilent dans la colonne de mercure, et pourtant les glaçons restent de glace.
Et là, oh surprise ! Après être montés à cinq degrés sans perdre leur intégritéintégrité, les glaçons commencent à fondre alors que la température de votre thermomètre entame une chute vertigineuse. Quelques minutes plus tard, vos glaçons ont fondu, mais l'eau qu'ils ont produit est maintenant à -5 degrés !
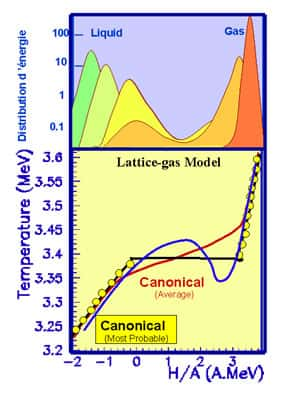
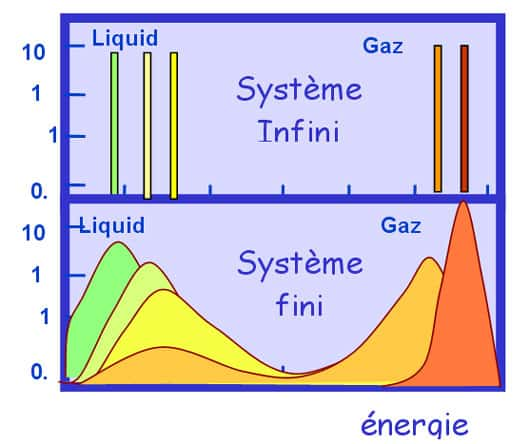
L'hésitation des glaçons lilliputiens entre l'état solideétat solide et liquide, et le paradoxe du système qu'il faut refroidir pour qu'il fonde, semblent à première vue deux absurdités décorrélées. Pourtant il s'agit de deux facettes du même phénomène. Les physiciensphysiciens représentent la possibilité des objets à se présenter sous des formes ou phases différentes en termes d'énergieénergie libre F=E-TS, qui est une espèceespèce de compromis entre la tendance des systèmes à s'installer dans l'état le moins perturbé possible, celui dans lequel l'énergie E est la plus faible, et la tendance opposée de l'agitation thermique à augmenter irréversiblement le désordre S. Graphiquement on peut se représenter ca comme un jeu de montagnes russes.
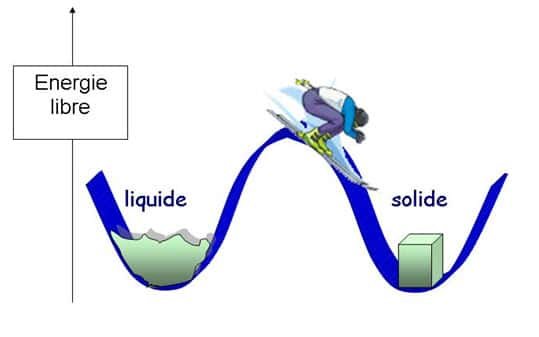
Image d'une transition de phase du premier ordre
A la température de transition, le système dans l'état liquideétat liquide est autant à l'équilibre (son énergie libre est minimale) que dans l'état solide. Les deux solutions sont exactement équivalentes seulement à cette température, mais pour des températures pas trop éloignées les deux vallées continuent à exister. La hauteur de la barrière d'énergie libre qui sépare les deux états est proportionnelle aux nombre de particules du système, elle est donc pratiquement infranchissable pour les objets macroscopiques. Par contre dans des tout petits systèmes une fluctuation thermique peut être suffisante pour faire traverser la barrière au système : d'où l'hésitation des nos glaçons entre les deux états. Si le système se trouve à haut de la montagne comme le skieur de notre dessin, il est dans une situation instable : c'est la chaleurchaleur spécifique négative.