au sommaire

Astronomes contre Thermodynamiciens, ou de la faiblesse des Théorèmes
La raison d'une telle hostilité réside dans le fait que deux théorèmes fondamentaux sur lesquels repose la thermodynamique toute entière s'opposent catégoriquement à la possibilité d'une capacité calorifique négative. Le premier théorème (théorème de Schroedinger) (voir 2*)) adresse la relation fondamentale entre les équations d'état et les observables, et démontre en particulier que la capacité calorifique pour un système en contacte avec un réservoir à température TT est donnée par la fluctuation d'énergie divisée par le carré de la température, quantité qui ne peut être négative.

Gauche : l'ensemble canonique dans la vie de tous les jours. La température est contrôlée par le contacte thermique avec le four. Droite : l ‘ensemble microcanonique : la quantité de chaleur est contrôlée par la cuisinière.
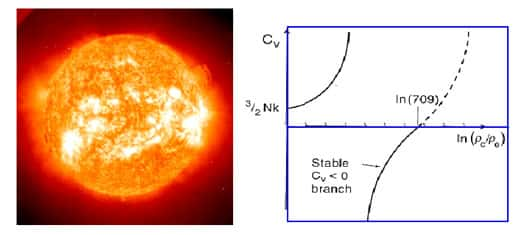
Or justement un système a capacité calorifique négative ne peut pas s'équilibrer avec un bain thermique. En effet éloignons nous des frigos lilliputiens et rendons nous cette fois au pays des TitansTitans. Que se passe-t-il si l'on met notre étoile dans un four titanesque ? L'étoile étant initialement plus froide que le four, le four va essayer à la réchauffer, c'est-à-dire que la différence de température entre les deux objets induit un flot d'énergie du four vers l'étoile, ce qui va encore plus diminuer sa température et l'éloigner de celle du four.
Impossible de préparer des rôtis d'étoile dans le monde des Titans !
L'impossibilité d'équilibre entre notre système et le thermostatthermostat ne signifie toutefois pas que l'équilibre du système tout court soit impossible. En effet un système isolé comme une étoile ou un noyau atomique se désintégrant dans le vide, peut très bien se trouver à l'équilibre dans le sens que tous les micro-etats compatibles avec l'énergie du système sont équiprobables (voir encadré).
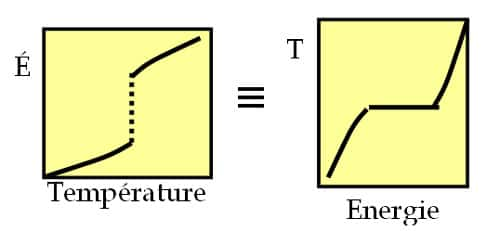
Représentation schématique de l'équivalence entre ensembles : contrôler la température et mesurer l'énergie (gauche) conduit à la même courbe calorique, c'est à dire la même relation entre énergie et température, que en contrôlant l'énergie et mesurant la température (droite).
Dans une telle situation, connue en mécanique statistique sous le nom d'ensemble micro-canonique, la température est autant bien définie que si le système est mis dans un four (ensemble canonique) ; un thermomètrethermomètre placé à l'intérieur d'un système isolé mesure une température donnée par l'inverse de la variation du logarithme du nombre d'états par rapport à l'énergie.

Gauche : J.W.Gibbs (1839-1903) introduit le concept d'ensemble en mécanique statistique. Droite :E.Schroedinger (1887-1961), l'un des pères de la mécanique quantique, prix Nobel 1933, fait dans notre histoire une toute fugace apparition à propos de fours et casseroles
Tout va bien alors. Un système isolé est un système micro-canonique et le théorème de Schrödinger 2 ne s'applique pas aux systèmes micro-canoniques, ce qui laisse à notre étoile la possibilité de se refroidir quand on la chauffe.
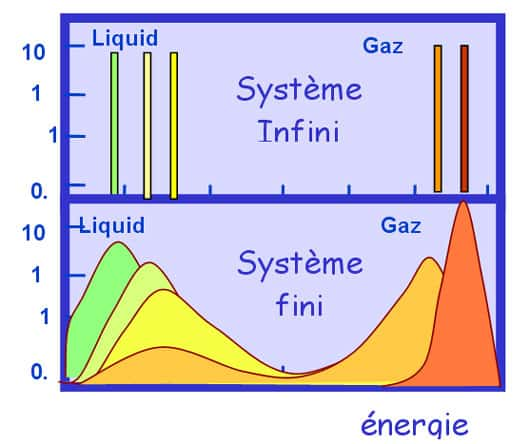
Mais voilà qui intervient le deuxième théorème (théorème de Van Hove) /3/ qui nous assure que tous les ensembles sont équivalents en moyenne, c'est à dire que un système isolé et le même système placé dans un four doivent montrer la même dépendance fonctionnelle entre température et énergie (techniquement on dit qu'ils obéissent à la même équation d'état). Toute la thermodynamique étant construite sur cette prétendue équivalence, on comprend maintenant comme la possibilité d'une capacité calorifique négative a pu être niée avec une certaine vigueur.
La solution de ce problème réside dans le fait que pour démontrer qu'il est équivalent d'exciter un système en le posant dans un four ou en lui déposant une quantité définie d'énergie, il est nécessaire de négliger explicitement l'énergétique des interfaces. Or ceci est possible seulement si les corrélations entre particules ont une portée infiniment plus petite de la taille du système : dans ce cas, et dans ce cas seulement, une portion arbitraire du système est une réplique statistique du système total (on dit techniquement que le système est extensif). En particulier dans le cas d'un système autogravitant l'influence de l'interaction gravitationnelle qui lie ses constituants est ressentie même à une distance infinie. L'équivalence des ensembles n'est donc pas valable pour ces systèmes et toute la thermodynamique perd son pouvoir prédictif.
2 E.Schroedinger, 'Statistical Thermodynamics', Cambridge (1952).
3 C.N.Yang, Phys.Rev. 85 (1952) 809
| Encadré I : Equilibre et ensembles statistiques |
En physique statistique nous appelons micro-état chaque réalisation d'un système physique. Si le système est composé de N particules, le micro-état est l'ensemble des positions et des vitesses de toutes les particules à un instant donné : on peut le représenter comme un point dans un espace à 6xN dimensions (1) 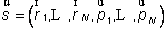 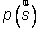 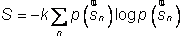 Tout système physiquephysique évolue spontanément vers le désordre, ce qui signifie que l'entropieentropie est maximale à l'équilibre. Plus l'énergie donnée à un système est élevée, plus le nombre d'états possibles sera grand. L'entropie augmente donc avec l'énergie, et l'importance de cette augmentation est mesurée par la température selon la formule de Clausius 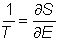 qui montre que plus la température est faible, plus l'ajout d'énergie engendre le désordre. La condition que le désordre soit maximal à l'équilibre définit de façon complète la distribution des micro-états, c'est à dire la valeur de probabilité avec laquelle chaque état se présente en nature. Si le système est isolé (il ne peut échanger ni énergie ni matièrematière avec le monde extérieur), alors il est possible de démontrer que tous les états sont associés à la même probabilité, et l'entropie résulte 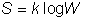 Où W est le nombre total de micro-états possibles. Nous appelons cette situation l'ensemble microcanonique . Si par contre le système se trouve en contact thermique avec le monde extérieur, il peut donc échanger de l'énergie avec son entourage, alors à l'équilibre la probabilité d'observer le système dans le micro-état 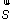 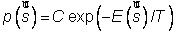 On peut dire alors que le système est décrit par l'ensemble canonique et nous appelons cette expression la distribution de Boltzmann. Quand le système est infiniment étendu (limite thermodynamique), cette probabilité devient la même pour tous les états avec un contenu énergétique E0 défini par la température du système, et nulle pour tous les autres. On retrouve alors les mêmes probabilités que pour le cas du système isolé, et les physiciensphysiciens disent que les ensembles canonique et microcanonique sont équivalents. (1) Pour être plus précis, quand il s'agit d'objets microscopiques comme nos glaçon lilliputiens, un point n'est pas suffisant pour spécifier l'état du système, qui doit se représenter comme une onde dans l'espace des positions des particules, 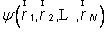 |