au sommaire
C'est une petite tablette d'argileargile de quelques centimètres de côté. Un objet tout simple qui tient dans le creux de la main et sur lequel ont été tracées quelques lignes et gravées quelques marques. Cette tablette se trouve à l'université de Yale, aux États-Unis, répertoriée sous le nom de YBC 7289 (Yale Babylonian Collection)).

Tablette YBC 7289, la plus ancienne représentation de la racine carrée de 2
Probablement l'œuvre d'un scribe babylonien de la première dynastie, soit entre 1900 et 1600 avant notre ère, elle n'est rien de moins que l'acte de naissance de la racine carrée de 2 en tant qu'objet mathématique, ainsi que l'une des plus anciennes incursions de l'humanité dans le monde de la pensée scientifique.

Il n'est pas très difficile de traduire cette tablette, écrite dans la langue la plus universelle qui soit : les mathématiques. En voici une translittération dans notre système moderne de numération (avec d'inévitables arrondis dus au fait que les Babyloniens utilisaient un système de représentation des nombres à base 60 et non à base 10 comme nous le faisons aujourd'hui).
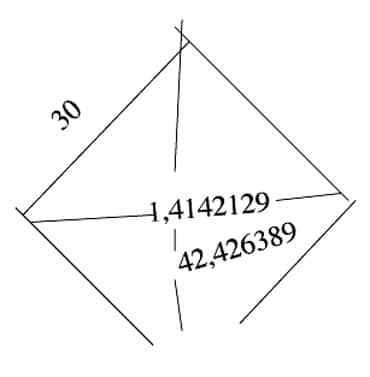
Le sens de la tablette YBC 7289 tel que nous pouvons le reconstituer est le suivant : un carré de côté 30 étant donné, la longueur de sa diagonale s'obtient en multipliant 30 par la valeur 1,41421296, ce qui donne 42,4263889.
Une valeur à portée universelle
Contrairement à la longueur du côté, sans doute choisie égale à 30 dans le simple but de donner un exemple concret, la valeur 1,41421296 que les Babyloniens ont mise en évidence a une portée universelle : c'est cette valeur qu'il faut utiliser pour trouver la diagonale de n'importe quel carré, quelle que soit la longueur de son côté. Bien loin d'une simple grandeur géométrique juste présente à l'occasion d'un exercice, la valeur 1,41421296, qui est pour nous la racine carrée de 2, figure dans YBC 7289 en tant que constante fondamentale de la géométrie. Ce statut est toujours le sien aujourd'hui.
































