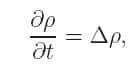La naissance : Gaspard Monge

Gaspard Monge (1746-1818) est un mathématicienmathématicien et ingénieur français de premier plan, spécialiste de géométrie.  Ardent révolutionnaire, fondateur de l'École Polytechnique, participant clé de la campagne d'Égypte, ami intime de Napoléon Bonaparte, Monge mène une vie de personnage de roman, tout en imprimant sa marque durable sur les mathématiques.

Son plus haut fait de gloire est peut-être la théorie de la géométrie descriptive, longtemps restée un pilier de la formation scientifique des  ingénieurs ; l'armée française de la fin de l'Ancien Régime avait si bien reconnu le potentiel énorme de cette théorie qu'elle l'avait, dit-on, classée "secret-défense''.

C'est en 1781 que Monge formule le problème de transport optimal, plus comme un ingénieur que comme un mathématicien ou un économiste. Les ressources à transporter sont par exemple des matériaux de constructionconstruction, extraits d'une mine, et que l'on utilisera pour un certain ouvrage. Pour reprendre la formulation de Monge, exemplaire de clarté et de précision :

Lorsqu'on doit transporter des terres d'un lieu dans un autre, on a coutume de donner le nom de déblai au volume des terres que l'on doit transporter, et le nom de remblai à l'espace qu'elles doivent occuper après le transport.

Le prix du transport d'une molécule étant, toutes choses d'ailleurs égales, proportionnel à son poids et à l'espace qu'on lui fait parcourir, et par conséquent le prix du transport total devant être proportionnel à la somme des produits des molécules multipliées chacune par l'espace parcouru, il s'ensuit que le déblai et le remblai étant donnés de figure et de position, il n'est pas indifférent que telle molécule du déblai soit transportée dans tel ou tel autre endroit du remblai, mais qu'il y a une certaine distribution à faire des molécules du premier dans le second, d'après laquelle la somme de ces produits sera la moindre possible, et le prix du transport total sera un minimum. C'est la solution de cette question que je me propose de donner ici.

Si l'on reprend les termes de Monge, on constate que son problème de <<transport au moindre coût>> est basé sur les éléments suivants :

- une distribution de masse initiale, et une distribution finale ; pour des raisons évidentes leur masse totale doit être la même.

- une fonction de coût : en l'occurrence Monge suppose que le prix du transport est proportionnel à la distance que l'on fait parcourir.

La distribution initiale est la quantité de matériau que l'on peut extraire, en fonction de la position (à tel endroit on ne peut pas creuser profond, à tel autre si, etc...) La distribution finale est la distribution que l'on veut, que la matière occupe à la fin du transport. Quant à la fonction de coût, appelons-la c(x, y), où x est le point de départpoint de départ et y le point d'arrivée : pour transporter un grain de matière de masse m du point x au point y, on va payer un coût mc(x, y). Monge définit c(x, y) comme égal à la distance entre les points x et y, ce qui est le choix le plus naturel mais n'est pas du tout innocent.

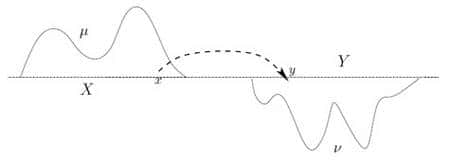
Et l'inconnue dans le problème de Monge est l'applicationapplication de transport, disons T, qui nous dit quelle est la position y=T(x) où nous devons transporter la masse située en x, de manière à ce que le coût total de transport soit minimal. Ce coût total est donné par la formule :

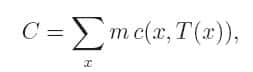
c'est-à-dire que c'est la somme des coûts de transport de toutes les particules individuelles. Pour les plus mathématiciens des lecteurs, la formule correcte donnant le coût total de transport est :

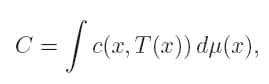
où  µ est une mesure de probabilité représentant la distribution de masse initiale ; et la contrainte de transport est T_#µ = ∨ (la mesure image de µ par T est ∨), ∨ désignant la distribution de masse finale.

Monge apparaît trop sûr de lui quand il annonce qu'il va résoudre le problème. Dans son mémoire, il obtient des solutions particulières, des algorithmes de calcul pour certaines géométries simples, fait le lien avec des découvertes géométriques remarquables (lignes de courbure des surfaces convexesconvexes...), mais ne résout pas le problème général, qui sera d'ailleurs mis à prix par l'Académie des Sciences.

Et pour cause : la simple existence d'une solution au problème de Monge, pour des données assez générales, ne sera démontrée qu'à la fin du vingtième siècle ! Quant à construire "explicitement'' cette solution (par exemple au moyen d'un ordinateurordinateur), c'est un problème toujours d'actualité, pas encore pleinement résolu. Pour progresser sur ces questions, il a fallu des outils beaucoup plus puissants que ceux dont disposait Monge.