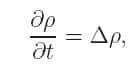
Le grand boom

Dans le milieu des années 90, les idées de Brenier sont étudiées au Canada, en Allemagne aux états-Unis.

Avec le regain d'intérêt pour ces questions, on se penche aussi sur les articles de Monge. Craig Evans et Wilfrid Gangbo aux états-Unis, Neil Trudinger et Xu-Jia Wang en Australie, Luigi Ambrosio en Italie, trouvent indépendamment, et par trois méthodes différentes, des démonstrations rigoureuses de l'existence d'une solution au problème de Monge.

C'est à la suite de nombreuses discussions avec Brenier, puis après avoir assisté à un exposé enthousiasmant de Craig Evans à Paris, que je décide de m'impliquer à fond dans le sujet.

Une autre rencontre décisive pour moi est celle de Felix Otto, en 1998. Il est alors en train de continuer à explorer les conséquences d'une découverte fascinante qu'il a faite quelques années auparavant avec Richard Jordan et David Kinderlehrer, et dont je vais tenter de donner une idée.

Considérons un grand nombre de particules qui évoluent "au hasard'', indépendamment les unes des autres, chacune selon une trajectoire brownienne,

A lire : Refroidir les ordinateurs avec le mouvement brownien

et mesurons, en fonction du temps et de l'espace, la densité de ces particules. On sait (c'est la découverte majeure faite au tournant du siècle précédent, indépendamment par Louis Bachelier, Albert EinsteinEinstein et Marian Smoluchowski) que cette densité est solution de l'équation de la chaleur.

L'équation de la chaleur (Fourier, 1822) est l'une des plus célèbres équations de la physique :

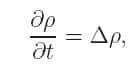
où ρ=ρ (t,x) est une fonction dépendant de deux variables t (temps) et x (position), d/dt désigne la dérivée par rapport à t, et

est le laplacien (par rapport à x ). Cette équation régit aussi bien (dans des conditions physiques adéquates) l'évolution d'une densité de particules (ρ  la densité de particules au temps t et au point x), que celle de la température dans un corps conducteur ( ρ la température au temps t et au point x).

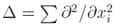
Voici maintenant comment peut s'exprimer la découverte d'Otto et de ses collaborateurs : considérons (c'est une expérience de pensée) un autre fluide fait d'un très grand nombre de particules, qui maintenant interagissent collectivement, et de manière à ce que l'énergie libre diminue le plus vite possible : il s'agit donc d'une version dynamique des principes de thermodynamique d'équilibre.

Eh bien, le résultat est le même que dans la première expérience : les particules évoluent encore selon l'équation de la chaleur !

L'énergie libre est une quantité thermodynamique, qui pour un gazgaz de particules classique est définie par E - TS où E est l'énergie cinétiqueénergie cinétique, T la température, et S l'entropieentropie. La diminution de l'énergie libre est un avataravatar
de la loi de l'augmentation de l'entropie (Second Principe de la thermodynamiqueSecond Principe de la thermodynamique). 

Cette découverte n'est pas une simple curiosité, et des principes similaires peuvent être énoncés pour de nombreuses équations classiques de la physique mathématique. Bien sûr, la formulation donnée ci-dessus est imagée et floue. Une description précise demande pas mal de notions mathématiques... et une bonne dose de transport optimal !