Transport optimal et géométrie

Une avancée importante des années 2000 a consisté à marier le transport optimal avec des notions géométriques de courbure. En l'occurrence, c'est la courbure dite de Ricci qui est le plus à l'honneur.

La courbure est une quantité qui varie d'un point  à l'autre, utilisée pour quantifier le degré de "non-euclidianité'' d'une géométrie. La sphère est une surface de courbure positive, le plan euclidien est bien sûr de courbure nulle. L'espace hyperbolique quant à lui est de courbure négative.

Les géomètresgéomètres utilisent plusieurs notions de courbure, parmi lesquelles les plus populaires sont la courbure de Gauss et sa généralisation la courbure sectionnelle; la courbure scalaire ; et la courbure de Ricci. Une courbure positive indique une tendance des courbes géodésiques (trajectoires de la lumière, disons) à se rapprocher, tandis qu'une courbure négative indique une tendance de ces même courbe à s'écarter. Le principal fait de gloire de la courbure de Ricci est son rôle de premier plan dans les équations d'EinsteinEinstein de la relativité générale.

C'est dans ce cadre que se situent mes propres travaux, qui font suite à ceux de Cordero-Erausquin, McCann et Schmuckenschläger ; j'ai travaillé sur ces thèmes en collaboration avec John Lott, et en compétition cordiale avec Karl-Theodor Sturm (si on fait le compte : deux français, deux allemands, un canadien, un américain... il n'y a là rien d'extraordinaire : la recherche mathématique, non contrainte par la présence dans  des laboratoires bien définis, est la plus internationale qui soit).

Nos résultats principaux fournissent de nouvelles caractérisations de bornes inférieures sur la courbure de Ricci, en termes des propriétés qualitatives du transport optimal. Il y a des énoncés mathématiques très précis bien sûr, mais je vais expliquer leur contenu en prenant des libertés avec la rigueur.

Imaginons deux physiciensphysiciens discutant d'une expérience de pensée visant à déterminer si le monde dans lequel nous vivons est courbé positivement.

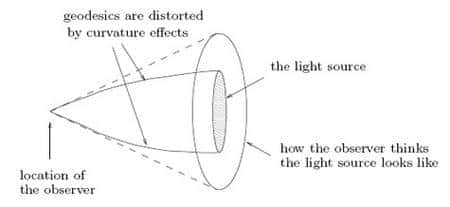
Voici une réponse classique. Quand j'observe une source lumineuse, l'image va être déformée par la courbure et je la verrai plus ou moins grande, comme sous l'effet d'un miroir déformant, ou d'un mirage. Si je surestime systématiquement la surface de la source lumineuse, c'est que je vis dans un monde à courbure (de Ricci) positive.

Fig. 3. En courbure positive, les rayons lumineux ont tendance a converger vers l’observateur, qui de ce fait surestime la taille de la source lumineuse.

Voici maintenant une réponse plus hétérodoxe, dont la formulation rigoureuse fait intervenir le transport optimal ; je l'appelle l'expérience du gaz paresseuxparesseux.

Soit un gaz avec une certaine répartition de densité : par endroits très dense, par endroits presque du vide... je lui impose une nouvelle répartition de densité, et toutes les moléculesmolécules doivent se mettre en branle pour se conformer à mon diktat ; la nouvelle répartition doit être obtenue au bout d'une minute. Le gaz obéit, mais comme il est paresseux, il va le faire en choisissant des mouvementsmouvements de molécules qui lui demanderont le moins d'efforts possibles (c'est ce qu'on appelle un chemin de moindre action). Durant tout le processus, je mesure l'entropieentropie du gaz, selon les formules de thermodynamiquethermodynamique classique. Je trace cette fonction entropie au cours du temps : si c'est toujours (c'est-à-dire indépendamment du choix de densité) une courbe concaveconcave, alors je vis dans un monde à courbure positive.

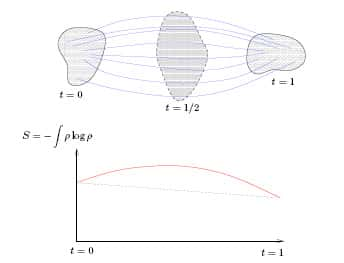
Fig. 4. Le gaz évolue selon un mouvement de moindre action ; on mesure son entropie à chaque instant et on vérifie que cette quantité varie de manière concave.

L'action d'un mouvement du gaz est définie comme l'intégrale, au cours du temps, de la somme des énergies cinétiquesénergies cinétiques de toutes les particules du gaz. Un chemin de moindre action est un écoulement tel que l'action est la plus petite possible (les états initiaux et finaux étant donnés).

On a vu ici l'équivalence en un certain sens d'un énoncé géométrique et d'un énoncé qui semble relever de la physiquephysique statistique, apparemment sans aucun lien. Cette équivalence n'est pas anodine et a de nombreuses conséquences.