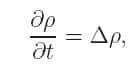La redécouverte : Leonid Kantorovich

Leonid Kantorovich (1912-1986) est un mathématicienmathématicien russe de renom. Sa vie présente plusieurs points communs avec celle de Monge : tous deux sont devenus professeurs à un âge remarquablement précoce.

Tous deux ont eu à s'opposer aux autorités politiques de leur temps et ont vu certains de leurs travaux frappés par le secret défense ; tous deux étaient de brillants théoriciens très intéressés par les applications pratiques et l'organisation de la société, à tel point que Kantorovich recevra en 1975 le Prix Nobel d'économie pour ses travaux sur le partage des ressources !

Des travaux qui sont directement en rapport avec le problème de transport optimal... Une entreprise l'ayant consulté pour améliorer son organisation interne, Kantorovich redécouvre à cette occasion (sans le savoir) le problème de coût minimum posé par Monge. Il introduit alors deux avancées fondamentales :

- il reformule le transport optimal comme un problème linéaire,

- il introduit un problème dual, qui aura des répercussions fondamentales aussi bien en mathématiques qu'en économie.

Qu'entend-on par problème linéaire ? Pour caricaturer, dans l'approche de Kantorovich on minimise la quantité

où x est le point de départpoint de départ, et y le point d'arrivée ; à comparer à comme faisait Monge. Supposons que les unités de production sont encodées par des nombres a_1,... a_N (pour reprendre notre analogieanalogie précédente, a_i est la quantité de croissants que produit la boulangerie B_i) et les unités de consommation par des nombres b₁,... b_m (b_j est la quantité de croissants consommés dans le café C_j). Alors l'inconnue dans le problème de Kantorovich est une matrice (p_ij)où chaque p_ij représente la quantité de croissants produite en i et acheminée en j.  Bien sûr on doit avoir d'une part :

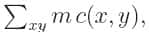
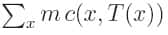
et le problème consiste à minimiser le coût total

où c_ij est le coût de transport d'un panier de croissants B_i de la boulangerie au café C_j.

L'observation cruciale de Kantorovich est que les équations (1) et (2), ainsi que la quantité à minimiser (3), sont des fonctions "linéaires'' des inconnues p_ij! Plus précisément, si (p_ij) et (p'_ij) sont deux solutions (deux façons différentes de réaliser le transport au moindre coût), alors la demi-somme (p_ij + p'_ij)/2 sera également solution.

Kantorovich comprend que de nombreux problèmes importants présentent cette même structure, et développe des méthodes efficaces pour les résoudre : c'est la naissance de la programmation linéaire, qui joue aujourd'hui un rôle vital en algorithmiquealgorithmique.

La dualité de Kantorovich est également la manifestation de cette structure linéaire. Pour l'expliquer, je vais continuer l'analogie dans la même veine que précédemment: vous faites tourner votre affaire de croissants, boulangeries et cafés, quand un jour se présente un entrepreneur qui vous propose de lui sous-traiter le problème du transport. <<Ne vous inquiétez pas, vous dit-il, vous me donnerez simplement tous les chiffres de production et de consommation, et je me chargerai de votre transport. Je viendrai acheter la marchandise aux boulangeries, je la revendrai aux cafés. Et pas d'embrouille : le prix que je demanderai à l'arrivée ne sera jamais plus élevé que la somme du prix d'achat et du prix de transport ! vous avez donc intérêt à me laisser carte blanche.>>

Bien entendu, vous acceptez le marché: vous êtes forcément gagnant. Le problème de l'entrepreneur, maintenant, est de fixer des prix appropriés. Il doit respecter sa promesse (la différence entre prix de vente et prix d'achat ne doit jamais excéder le coût du transport), mais en même temps son intérêt est de fixer les prix les plus élevés possibles ; ou plus précisément, de fixer les prix de façon à obtenir un profit maximal.

Nous avons donc un nouveau problème d'optimisation : les inconnues sont des prix u₁, u₂, ... (u_i est le prix d'achat à la boulangerie B_i) ; et des prix v₁,v₂,...  (v_j est le prix de vente au café C_j). La contrainte est :

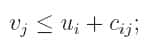
(le prix d'arrivée n'excède jamais la somme du prix d'achat et du prix de transport), et le problème est de maximiser le "profit'':

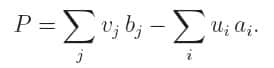
Le théorème de Kantorovich énonce que le résultat est le même que celui du transport optimal ! Avec les notations ci-dessus,

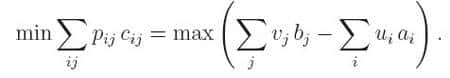
Autrement dit, l'intermédiaire peut se débrouiller pour empocher exactement la somme que vous auriez dépensée en faisant le transport vous-même!

Pour les lecteurs avertis : Le théorème de dualité de Kantorovich, énonce de manière plus précise, stipule que sous des hypothèses ad hoc (très générales),

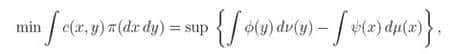
où c (x,y) est le coût de transport entre x et y, 

(x) et  (y) les prix d'achat et de vente en x et y respectivement ; µ est v sont deux mesures de probabilité  représentant  les distributions initiale et finale ; π (dx dy) est une mesure de probabilité jointe dont les marginales sont égales à µ(dx) et v(dy) respectivement ; et ,  sont liées par la contrainte  (en tout x et en tout y).

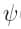
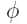
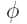
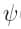
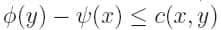
Les contributions de Kantorovich sonnent le début d'une ère prospère pour le transport optimal. Pendant des décennies, il sera utilisé avec succès par des économistes, statisticiens, probabilistes, ... avec le  théorème de dualité de Kantorovich en chef d'orchestre.