L'outil informatique

Jusqu'aux travaux d'Andrei Linde et de ses collaborateurs, la brisure spontanée de symétrie était étudiée à partir des théories des perturbations (très évoluées) mais dont les résultats étaient fortement non linéaires et sans effets perturbateurs. On obtenait bien la création de particules au terme du processus mais en nombre inversément proportionnel aux constantes de couplages. Son application était donc limitée et elle ne décrivait pas proprement la diffusion des particules dans l'univers et la production des défauts topologiques, inséparables de cette théorie.

Grâce à la collaboration du physicienphysicien théoricien Gary Felder de l'Université de Stanford, Andrei Linde put disposer de programmes capables de simuler des équations d'ondes relativistes dans un espace tridimensionnel en expansion. Ce programme tenait également compte des effets de la renormalisation et des effets quantiques de nature semi-classique.

Armé de cet outil performant Linde et son équipe parvinrent à simulation la phase de brisure spontanée de symétrie dans différents modèles chaotiques et purent avoir une vue plus claire de tout le processus.

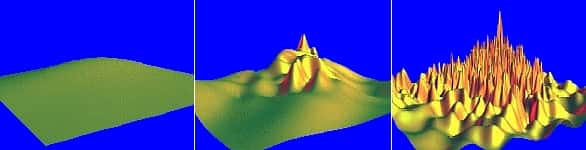
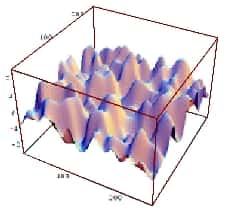
Pour expliquer la théorie la plus simple de brisure spontanée de symétrie, Andrei Linde et ses collaborateurs considèrent un champ scalaire homogène dont une composante est réelle et dont le potentiel d'énergie est nul. Après l'inflation ce champ subit encore des fluctuations quantiques autour de son minimum d'énergie. Ces fluctuations sont entretenues par des instabilités du champ qui dépendent fortement des conditions initiales du système. Le potentiel V de ce champ scalaire f présente une courbure non plus nulle mais négative. En d'autres mot la composante V(f) < 0. On parle dès lors d'instabilité "tachyonique" par référence à des particules dont la massemasse portée au carré est négative.

Dans le modèle inflationnaire standard, après l'inflation s'il y a une instabilité tachyonique ces oscillations s'arrêtent presque immédiatement, typiquement en l'espace d'une seule oscillation.

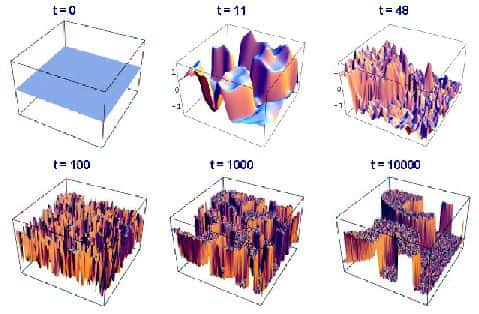
Ces instabilités tachyoniques ont la propriété bien particulière de provoquer une conversion de l'énergie potentielleénergie potentielle du champ en énergie de collision des ondes classiques du champ scalaire, phénomène appelé le "préchauffage tachyonique". Ce phénomène post inflationnaire provoque une brisure spontanée de symétrie jusqu'à former des domaines à une vitessevitesse exponentielle. Dans certains conditions particulières une seconde phase inflationnaire pourrait se produire après l'étape de préchauffage mais en général ce phénomène se produit après l'inflation.

Dans tous les cas ce processus ne peut pas se produire en l'absence de défaut topologiques. Il faut donc absolument que les physiciens des particules élémentairesparticules élémentaires découvrent ces particules exotiquesexotiques pour valider ce modèle.

La formation des domaines Evolution d'un processus de brisure spontanée de symétrie depuis les fluctuations du champ scalaire entretenues par des instabilités tachyoniques jusqu'à la formation des domaines. Document G.Felder, L.Kofman, A.Linde.

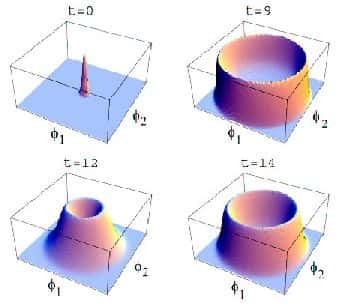
On peut également étudier cette phase de transition avec des composantes complexes du champ scalaire dont le potentiel d'énergie est également nul. Avec étonnement on constate alors que le champ tombe au minimum de son énergie potentielle effective à l'endroit où le champ est nul puis s'étend rapidement au cours de la première oscillation pour se stabiliser au moment de la brisure spontanée de symétrie. En d'autres termes, une partie non négligeable de l'énergie du faux vide est transférée au gradientgradient d'énergie du champ f au cours de sa chute vers son minimum d'énergie (le bas de la coliine). Mais dans son état initial le champ fluctuait très fort et les phases évoluaient à différents taux, si bien que l'énergie résultante était distribuée de façon si complexe que le champ n'a pas put revenir à son état d'énergie initial nul. C'est l'une des raisons qui ont permis à la brisure de symétrie de se produire et à la phase de préchauffage de se dérouler au cours d'une seule oscillation du champ f.

Quelle que soit pratiquement la distribution d'énergie à l'échelle de PlanckPlanck, les domaines grandissent et percolent (fusionnent), la brisure spontanée de symétrie étant établie à l'échelle macroscopique.

Le phénomène de brisure de symétrie Processus de brisure spontanée de symétrie d'un champ scalaire homogène dont les composantes sont complexes. La brisure de symétrie se produit en l'espace d'une seule oscillation. Document G.Felder, L.Kofman, A.Linde.

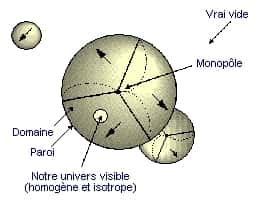
Parmi les implications de ces découvertes, il faut noter qu'au cours du transfert de l'énergie du faux vide au gradient du champ f il existe un niveau critique f_c appelé "point de bifurcationbifurcation" où l'inflation s'arrête et à partir duquel les champs tombent rapidement vers leur état d'énergie minimum, le vrai vide. Pour certaines valeurs de densité d'énergie s on aboutit à la formation de domaines murés (domain walls), c'est-à-dire de régions de l'espace séparées les uns des autres et obéissant à des lois physiquesphysiques totalement différentes. Pour éviter ce problème, il faut considérer que la composante s de la densité d'énergie est un champ complexe. Dans ce cas la brisure de symétrie qui se produit à la fin de l'inflation produit des cordes cosmiques plutôt que des domaines murés.

Enfin Linde conclut que dans des versions réalistes de ce modèle le régime tachyonique (relaxe du champ en une seule oscillation) est lié à la géométrie du champ scalaire qui présente une courbure négative. Mais appliqué à une inflation hybridehybride tenant compte de la gravitationgravitation dans la cadre de la théorie de la supersymétriesupersymétrie SUSY, la relaxe du champ s'établit en général après plusieurs oscillations, ce qui ne permet pas d'aboutir à la création des particules.

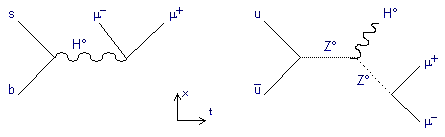
Mais le préchauffage tachyonique semble toutefois être une propriété de cette inflation hybride, du moins si le champ d'énergie ne descend pas trop rapidement vers le point de bifurcation. Ce processus est en effet capable de produire des bosonsbosons (ces vecteurs comme le graviton ou le photonphoton véhiculant les interactions entre particules) à partir de la production et la dispersion d'ondes classiques du champ d'énergie scalaire. Mieux encore, la nature tachyonique du préchauffage implique la production de gravitinosgravitinos (gravitons supersymétriques), non pas par un champ oscillant cohérent mais par la dispersion d'ondes classiques dans les champs scalaires. Ce phénomène pourrait expliquer la génération de l'asymétrie des baryonsbaryons à l'échelle d'énergie de la théorie électrofaiblethéorie électrofaible (10¹⁵ GeVGeV).