Effet EPR : le monde quantique ne peut être construit qu'avec des nombres complexes

Il y a quelques semaines, Futura vous parlait d'un des tout derniers ouvrages grand public publiés par Carlo Rovelli au sujet du mystérieux Monde quantique et intitulé Helgoland. Dans celui-ci, il était notamment exposé la thèse que l'approche entreprise par Heisenberg pour décrire le comportement général de la matière et son interaction avec la lumière était plus profonde que celle initiée par Louis de BroglieLouis de Broglie et EinsteinEinstein, magistralement développée dans une série d'articles impressionnants par Schrödinger, où celui-ci avait trouvé l'équation d'onde portant aujourd'hui son nom.

De la même façon qu'en son temps la découverte par Newton du calcul infinitésimal avait permis la révolution de la science classique, c'est en remplaçant les quantités physiques de celle-ci initialement décrite à l'aide des nombres réels par des tableaux de nombres et des équations relevant de ce que les mathématiciensmathématiciens du XIX^e siècle ont appelé le calcul matriciel, après sa découverte, que les idées de Heisenberg ont été rapidement développées.

Les matrices de Heisenberg contenaient des nombres complexes et surtout, comme Max BornMax Born allait le montrer, devaient vérifier une algèbre non commutative avec ces nombres, impliquant que l'ordre du produit de deux matrices associées aux coordonnées X de position et P d'impulsion d'une particule de matière était important. Permuter le produit de ces matrices ne donnait pas le même résultat, de sorte que la différence des deux produits était une matrice dite unité, que multipliait un nombre complexe, plus précisément le nombre imaginaire « i ».

Symboliquement, Born arrivait à la conclusion que XP-PX = i (h/2π) où h est la fameuse constante d'action de PlanckPlanck, introduit pour rendre compte de la loi du corps noircorps noir et clé de l'atome de Bohratome de Bohr.

Le physicienphysicien théoricien Paul DiracPaul Dirac, le découvreur entre autres de l'antimatièreantimatière, allait au même moment décrire la révolution de Heisenberg et Born en développant l'idée que pour passer des lois de la physique classique aux lois de la mécanique quantiquemécanique quantique, il fallait passer des c-nombres de la mécanique classique, les nombres réels et les fonctions de nombres réels, à des q-nombres ne reposant pas sur une algèbre commutative.

L'équation de Schrödinger et les nombres complexes

Peu de temps après, Schrödinger découvrait son équation gouvernant les ondes de matière de Louis de Broglie et, de prime abord, restaurait une approche intuitive des phénomènes atomiques. Les matrices de Heisenberg n'avaient pas d'interprétation naturelle évidente en matière d'images classiques dans l'espace et le temps. De fait, Heisenberg avait également mis au centre de son travail l'idée qu'il fallait rejeter ces images pour se concentrer sur la description mathématique des phénomènes directement observables.

Toutefois, et alors que bien des physiciens voyaient la mécanique ondulatoiremécanique ondulatoire de Schrödinger avec soulagement, il ne lui avait pas échappé que son équation faisait directement intervenir un nombre complexe et donc parfois des solutions avec des nombres complexes. Pour lui, comme il l’expliquait dans un des articles qu’il avait développés en 1926 sur sa théorie, il fallait probablement en conclure que la véritable équation des ondes de matière restait encore à découvrir et que celle-ci ne ferait plus intervenir de nombres complexes.

Tous les apprentis physiciens qui étudient la théorie quantique savent que les équations de Heisenbergéquations de Heisenberg et Schrödinger, dont on peut montrer qu'elles sont deux formulations équivalentes d'une même structure en pratique dans leur forme la plus générale exposée par Dirac, font intervenir des nombres complexes. Mais ils peuvent parfois se poser la même question que Schrödinger et d'autres après lui. Ne peut-on pas à chaque fois, bien que les calculs soient plus complexes et moins faciles à faire, appliquer la théorie quantique en utilisant uniquement des nombres réels ?

En fait, il existe bien des calculs en physique classique, notamment en théorie des ondes ou avec ce que l'on appelle l'équation du potentiel utilisée en électrostatiqueélectrostatique, hydrodynamique, théorie de la chaleurchaleur et de la gravitationgravitation newtonienne où les équations ne font pas intervenir de nombres complexes mais où la version du calcul infinitésimal de Newton avec des nombres complexes, et ce que l'on appelle des fonctions holomorphes exceptées en quelques points singuliers, font des merveilles pour résoudre ces équations.

Mais il ne s'agit que d'astuces très puissantes et élégantes pour abréger les calculs et les démonstrations, en aucun cas un ingrédient fondamental de la réalité. Alors qu'en est-il finalement en théorie quantique ?

Comme expliqué dans la vidéo ci-dessus, les nombres complexes peuvent être identifiés à des points du plan de coordonnées (x,y) et tout nombre complexe z pour ces points peut aussi se représenter sous la forme z = x + i y. On peut opérer sur ces nombres comme avec des nombres réels, à ceci près que le carré de « i »  donne  « -1 ».  Ainsi, un nombre complexe est en partie au moins un couple de deux nombres réels.

L'équation de Schrödingeréquation de Schrödinger est linéaire, de sorte que ses solutions peuvent s'additionner comme le feraient des vecteurs à n composantes. Ces vecteurs forment un espace vectoriel abstrait que les mathématiciens appellent un espace de Hilbert. On peut donc penser qu'un vecteur avec n composantes complexes est équivalent à un vecteur avec 2n composantes avec des nombres réels. Les matrices étant précisément aussi LE calcul avec des objets linéaires sur des espaces vectoriels, reformuler la mécanique quantique avec des espaces de Hilbert basés sur des nombres réels uniquement a été tenté, en doublant en quelque sorte la dimension des espaces de Hilbert.

Des résultats très encourageants en ce sens ont été obtenus à la fin des années 2009, laissant penser que l'on était sur le point de réaliser les espoirs de Schrödinger. Mais, en 2021, une équipe de physiciens parmi lesquels on trouvait Marc-Olivier Renou de l'Institut des sciences photoniques (ICFO), en Espagne, et Nicolas Gisin, professeur émérite au département de physique appliquée de l'université de Genève et bien connu pour ses travaux de pionnier sur la téléportation quantique, a montré théoriquement qu'il existait une expérience en physique quantiquephysique quantique qui potentiellement ne pouvait donner certains résultats que si les nombres complexes étaient bien une composante fondamentale et irréductible de la théorie quantique, pour le moins dans sa formulation standard (il existe des versions alternatives mais qui souffrent de problèmes non résolus d'une façon ou d'une autre).

L'intrication quantique et les nombres complexes

L'expérience en question fait intervenir le fameux phénomène d'intrication quantiqueintrication quantique découvert par Einstein et Schrödinger et qui est au cœur du fameux effet EPR discuté dans les deux vidéos sur la théorie quantique ci-dessus avec notamment des explications d'Alain AspectAlain Aspect sur les corrélations quantiques de l'effet EPR. On sait que cet effet conduisait lui aussi à une expérience permettant de tester l'idée déjà avancée par Einstein, de Broglie et Schrödinger que nous ne disposions pas encore d'une vraie solution aux énigmes de la mécanique quantique et que cette vraie solution devait faire intervenir un déterminisme aussi rigoureux qu'en mécanique newtoniennemécanique newtonienne. Les probabilités quantiques seraient alors un simple outil commode, comme celles de la théorie classique des gazgaz, pour décrire le comportement de la réalité avec des variables cachées, c'est-à-dire des informations manquantes sur les quantités mathématiques décrivant cette réalité comme les valeurs des positions et vitessesvitesses exactes de toutes les particules d'un gaz.

Le physicien irlandais John Bell était arrivé au cours des années 1960 à formuler clairement un test capable de réfuter la pertinence d'au moins une grande classe de théories à variables cachées. Au grand désappointement de Bell, qui espérait au contraire réfuter l'interprétion orthodoxe de la théorie quantique, c'est précisément cette réfutation qu'a obtenue une équipe de physiciens français dirigée par Alain Aspect au début des années 1980. Précisons toutefois que le résultat ne réfute pas toutes les théories à variables cachées possibles mais seulement celles qui sont "locales". La théorie quantique dite de Bohm-de Broglie redonne tous les résultats connus à ce jour concernant le comportement des atomes et des moléculesmolécules dans le domaine non relativiste tout en étant déterministe. Les problèmes qu'elle rencontre lorsque l'on cherche à en faire une version relativiste et pour la théorie quantique des champs n'ont pas vraiment été surmontés, selon l'avis de la majorité des physiciens.

Le schéma illustrant l'expérience proposée pour réfuter la formulation purement réelle de la mécanique quantique standard. Elle utilise des états quantiques dits de Bell décrivant des paires de particules intriquées venant de deux sources. Les particules étant distribuées à trois observateurs effectuant des mesures et pouvant les comparer à la recherche de corrélations statistiques. © APS, Carin Cain

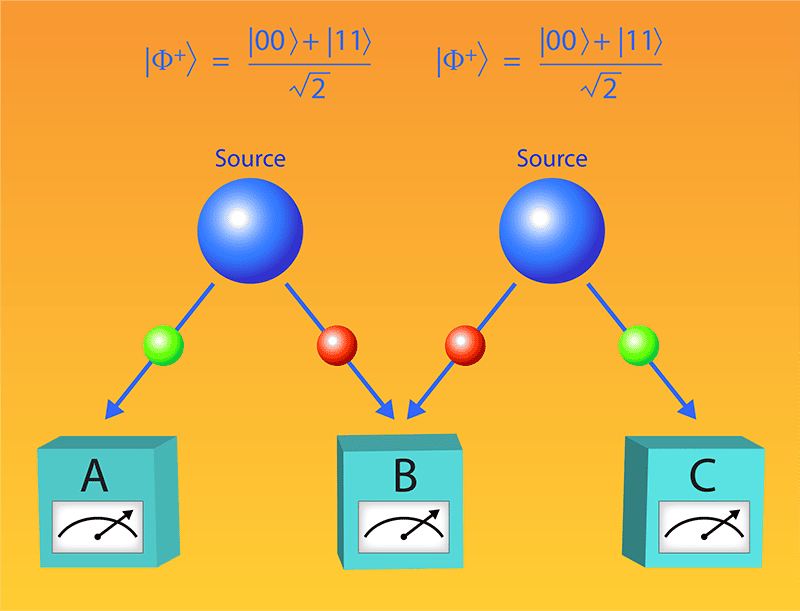
Tout comme dans l'expérience d'Alain Aspect, le test pour départager les versions avec nombres réels ou nombres complexes des équations standards de la mécanique quantique fait intervenir des paires de particules intriquées sur lesquelles on fait des mesures, mesures qui doivent exhiber des corrélations bien particulières.

Mais, cette fois-ci, ce sont deux paires de particules intriquées qui sont considérées et sujet de mesures faites par trois observateurs, Alice, Bob et Charles. A et B reçoivent une paire et B et C une autre. Toutefois, Bob peut faire des mesures sur la particule de la paire qu'il partage avec Alice et sur celle qu'il partage avec Charles, de telle sorte que toutes les particules sont maintenant un seul système de particules intriquées. L'opération qui permet de le faire s'appelle une mesure d'état de Bell.

On répète bien sûr plusieurs fois cette expérience et on analyse les corrélations entre les mesures faites par Alice et Charles qui sont maintenant mutuellement intriquées. La version purement réelle de la théorie quantique standard donne de façon étonnante des prédictions différentes de sa version avec des nombres complexes irréductibles.

Deux groupes de chercheurs ont monté deux expériences, différentes par les moyens mis en œuvre, mais testant selon le même principe exposé précédemment les deux versions de la théorie quantique. Les résultats ont été exposés dans deux articles que l'on peut trouver en accès libre sur arXiv.

L’équipe de Zheng-Da Li, qui a notamment pour membres Marc-OlivierOlivier Renou et Nicolas Gisin, a trouvé un écart de 4,5 sigmas, selon le jargon scientifique pour la théorie statistique des tests d'hypothèse, entre les résultats expérimentaux et les prédictions de la version avec espaces de Hilbert réels et donc un très bon accord avec la version avec des nombres complexes.

Utilisant donc un autre montage, ce qui garantit contre des erreurs systématiques, l’équipe de Ming-Cheng Chen a, elle, trouvé une violation spectaculaire d'environ 43 sigmas.

La cause semble donc entendue ou presque si l'on veut rester prudent et rigoureux, il n'y a pas moyen de rendre compte de la structure du monde quantique sans faire intervenir comme ingrédient fondamental des nombres complexes si l'on croit aux équations standards de la théorie quantique. Cela pourrait changer si d'autres équations étaient trouvées.

Des nombres complexes pour unifier les forces et quantifier la gravitation

Terminons en rappelant quelques perspectives intéressantes. Dans les années 1930, avec des collaborateurs, Einstein a démontré qu'il était possible de déduire les lois du mouvementmouvement de particules, chargées ou non, à partir des équations de la théorie de la relativité généralerelativité générale des espaces-tempsespaces-temps courbes, complétée de celles du champ électromagnétiquechamp électromagnétique de Maxwell dans ces espaces. En physique classique ce n'est pas le cas, les lois de la mécanique des points matériels ne se déduisent pas de la loi de la gravitation newtonienne, même dans la forme que Laplace et PoissonPoisson lui ont donnée.

Einstein espérait trouver une généralisation des équations de sa théorie relativiste de la gravitation qui non seulement unifierait la force électromagnétique et la gravitation, mais permettrait de déduire l'équation quantique du mouvement des points matériels chargés, c'est-à-dire l'équation de Schrödinger pour les électronsélectrons dans les atomes ou dans des expériences d'interférenceinterférence comme celle proposée par Richard FeynmanRichard Feynman.

Einstein étant bien conscient de l'existence des nombres complexes en mécanique quantique, il avait donc exploré des formulations d'extension d'équations de la relativité générale avec des nombres complexes. De nos jours et depuis les années 1960, le prix Nobel de physique Roger Penrose a lui aussi développé des théories quantiques de l'espace-temps faisant intervenir de façon fondamentale l'intrication quantique et les nombres complexes. Il a ainsi introduit sa théorie des réseaux de spinsspins, théorie que sera utilisée par Carlo Rovelli et Lee Smolin pour développer la théorie de la gravitation quantique à bouclesgravitation quantique à boucles, et surtout sa théorie des « twisteurs », comme il l'explique dans la vidéo ci-dessous.

Remarquablement, comme Futura l'expliquait dans un précédent article, Stephen HawkingStephen Hawking a utilisé les nombres complexes en gravitation quantique là aussi comme un ingrédient fondamental pour décrire un état de l'UniversUnivers très primitif avec le fameux modèle dit de Hartle-Hawking. Il ne s'agissait pas d'une simple astuce de calcul mais bien de la manifestation d'un changement d'état profond dans la géométrie de l'espace-temps.