au sommaire
Une pulsation cardiaque se passe en plusieurs temps. D'abord, les oreillettesoreillettes se remplissent de sang puis se contractent pour envoyer le liquideliquide dans la chambre suivante : le ventricule. À son tour, il se contracte et propulse son contenu dans le système circulatoire. Le cœur se repose le temps que les oreillettes se gorgent à nouveau de sang.
Pour un fonctionnement optimal, toutes ces phases doivent être bien coordonnées, ce qui n'est pas le cas lors d'une arythmie. L'anomalie la plus fréquente du rythme cardiaque s'appelle la fibrillation auriculaire, se manifestant par une désorganisation des cellules de l'oreillette, qui ne battent alors plus à l'unisson. À terme, cela peut déboucher sur des problèmes sérieux, comme des crises cardiaques.
La contraction des cellules auriculaires dépend des concentrations en calciumcalcium intracellulaire. Mais la dynamique est très complexe et les techniques actuelles ne permettent pas de visualiser ces variations en chaque point de la cellule.
Les scientifiques tentent donc d'utiliser des artifices pour mieux cerner ces mouvementsmouvements calciques, et des chercheurs de l'université de Nottingham (Grande-Bretagne) viennent de proposer dans les Pnas un modèle mathématique pour estimer plus précisément l'activité du calcium. Avec ces données supplémentaires, les auteurs misent sur le développement de nouveaux traitements contre ces pathologies.
Panique dans l’oreillette
À l'échelle d'une vie, le cœur peut subir plus de 2 milliards de contractions. C'est le ventricule qui est chargé d'envoyer le sang dans les artères mais au cours d'un effort physiquephysique, l'oreillette vient l'appuyer en lui donnant un peu de force supplémentaire. Or, avec l'âge ou lors d'un dysfonctionnement, les cellules de l'oreillette peuvent se détériorer et privent alors le ventricule de renfortrenfort lorsqu'il en a besoin.
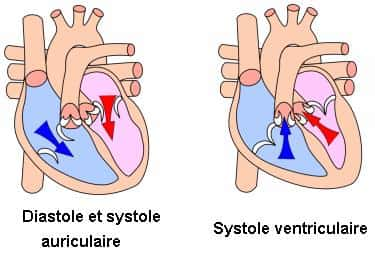
En diastole, les oreillettes (compartiments du haut) se remplissent de sang. Les valves auriculoventriculaires (en blanc) s'ouvrent lors de la systole auriculaire, et le sang passe des oreillettes aux ventricules. Elles se referment et lors de la systole ventriculaire, le sang est propulsé dans les artères. En bleu, le sang non oxygéné va rejoindre l'artère pulmonaire pour se recharger en O2. En rouge, le sang qui revient des poumons, riche en O2 envoyé dans tout l'organisme par l'artère aorte. © Wapcaplet, Wikipédia, cc by sa 3.0
Plusieurs études ont montré que pour enclencher la contraction des cellules auriculaires, la concentration de calcium suit une chorégraphie élaborée puisqu'elle diffère dans l'espace et dans le temps au sein d'une même cellule. Ce n'est pas du tout ce que l'on constate dans les cellules ventriculaires où la concentration calcique reste uniforme. Il devient donc fondamental de comprendre cette dynamique d'un point de vue global, à l'échelle cellulaire.
Des mathématiques au grand cœur
Le modèle mathématique proposé rend cette prouesse possible. « Il permet une exploration détaillée des modifications spatiotemporelles dans les concentrations de calcium associées aux situations saines et pathologiquespathologiques » commente Rüdiger Thul, l'un des scientifiques impliqués dans l'étude.
« En outre, nous pouvons activer, désactiver, surexprimer les propriétés cellulaires et regarder comment se comporte le calcium. Nous pouvons alors en déduire les conditions à l'origine d'anomalies pouvant conduire à certaines pathologies comme la fibrillation auriculaire » poursuit le mathématicienmathématicien.
Il faut garder en tête qu'un médicament agit toujours au niveau de la cellule. Un organe se porteporte mieux quand ses millions ou milliards de composants sont redevenus sains. Le modèle mathématique permet de disposer d'un modèle cellulaire complet en 3D et offre ainsi un terrain d'essai pour le développement de nouveaux médicaments.