au sommaire
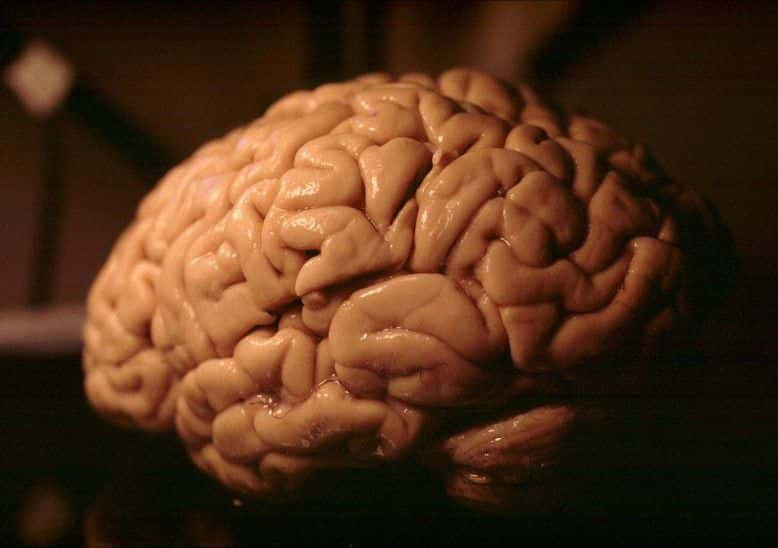
Au XIXe siècle, l'anatomiste Louis Pierre Gratiolet est l’un des premiers à décrire les circonvolutions cérébrales et à les nommer. © Heidi Cartwright/Wellcome Images/Flickr
L'image du cerveau humain, formé de creux et de bosses, nous est familière. Mais les processus qui régissent la formation de ces circonvolutions gardent encore une part de mystère. Une récente étude, publiée par le magazine Science et menée conjointement par des biologistes et des physiciensphysiciens de l'université de Rio de Janeiro (Brésil), apporte un éclairage nouveau... et surprenant. La loi mathématique qui décrit le froissement des feuilles de papier permettrait également de décrire les circonvolutions cérébrales ! La forme de notre cerveau ne serait donc pas le résultat d'une évolution subtile mais simplement le fait d'un processus physiquephysique des plus classiques.
Rappelons que le cerveau humain n'est pas le seul à présenter ce type de replis sinueux. Les cerveaux d'autres mammifèresmammifères, comme les chienschiens, les chats ou les éléphants, montrent également des circonvolutions. Objectif commun : augmenter la surface totale du cortex dans le volumevolume limité de la boîte crânienne. Pendant des décennies, les chercheurs ont tenté, en vain, d'établir un lien entre le nombre de ces circonvolutions et d'autres caractéristiques. Il n'existe ainsi, par exemple, pas de rapport entre le nombre de replis sinueux et le poids du cerveau ou le nombre de neurones.
Les chercheurs brésiliens ont travaillé sur des données issues de 62 espècesespèces différentes. Et ils ont établi une loi qui semble universelle et qui relie la surface totale du cortex et son épaisseur à la surface exposée. Comme la surface d'un cercle augmente en fonction du carré de son rayon, le produit de la surface totale du cortex et de son épaisseur augmente comme la puissance 1,25 de sa surface exposée. « En biologie, il est exceptionnel de trouver une relation mathématique qui corresponde aussi parfaitement à l'ensemble des données », souligne Georg Striedter, un neuroscientifique de l'Université de Californie interrogé par le magazine Science.
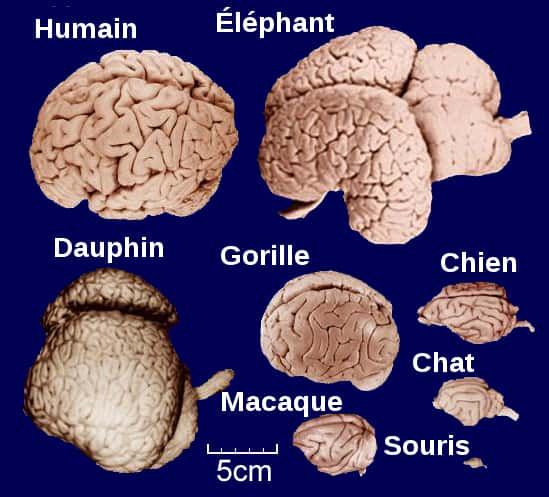
On dit de cerveaux qui ne présentent pas de circonvolution, comme celui de la souris, qu’ils sont lissencéphaliques. Par opposition, ceux qui en présentent des circonvolutions sont qualifiés de gyrencéphaliques. © Bourrichon/Wikipedia
L'origine des circonvolutions enfin expliquée ?
Et il se trouve que la loi en question est la même que celle qui décrit le froissement de feuilles de papier. Un résultat que la physique explique simplement par le fait que le papier froissé finit toujours dans la configuration qui minimise son énergie. En est-il de même pour notre cerveau ? La réponse n'est pas si simple. Car le papier froissé est soumis à des forces extérieures, celles appliquées par les mains. Le cortex, quant à lui, est plus vraisemblablement soumis à des forces internes qui restent, à l'heure actuelle, non encore clairement identifiées. Certains modèles, par exemple, supposent que le cortex externe grandit plus rapidement que le cortex interne, créant ainsi des circonvolutions observées.
Les chercheurs brésiliens proposent un point de vue différent. Selon eux, à chaque étape de son développement, le cortex est plus fortement soumis à la pressionpression extérieure du crânecrâne qui le contraint à se froisser, comme du papier. Une hypothèse qu'ils comptent bien soumettre à l'expérience en étudiant des cerveaux de porc à différentes étapes de leur développement. Si la relation mathématique évoquée plus haut reste valable au fil du temps, il n'y aura plus besoin de faire intervenir un autre processus pour expliquer les circonvolutions.