au sommaire
Quelles applications pour la relativité d'EinsteinEinstein ? Découvrez les plus surprenantes, comme la dilatationdilatation temporelle (paradoxe des jumeaux) par exemple.

Langevin : la dilatation temporelle et le paradoxe des jumeaux
La situation imaginée par Langevin est la suivante : deux frères jumeaux décident de faire une expérience grâce à une fuséefusée pouvant voyager à des vitesses proches de celle de la lumière. L'un d'entre eux reste sur Terre alors que l'autre part en voyage à une vitesse relativiste, puis, au bout d'un certain temps, fait demi-tour et revient vers la Terre à la même vitesse.
Le « paradoxe » consiste en ceci : lorsque le jumeaujumeau voyageur reviendra sur Terre, il sera plus jeune que son frère resté sur Terre. À partir de là, il existe plusieurs versions concernant « ce qui est paradoxal ».

La version la plus simple est celle où, selon le bon sens commun, le paradoxe réside dans le fait que des jumeaux devraient avoir le même âge toute leur vie. Pourtant, ceci repose sur une conception de temps absolu et universel, que la relativité renie entièrement. Ce n'est donc pas un paradoxe interne à la théorie.
En revanche, il peut paraître paradoxal que l'un des jumeaux soit finalement plus âgé que l'autre, car, a priori, rien n'interdit de se placer du point de vue du jumeau qui part dans la fusée et de considérer que c'est la Terre qui se déplace : depuis GaliléeGalilée déjà, le mouvement et la vitesse sont relatifs. Ainsi, selon un principe de symétrie, on devrait s'attendre à ce que chacun des jumeaux puisse faire le même raisonnement et on ne saurait conclure qui des deux sera réellement plus âgé, ni même s'il y en aura un plus âgé. Or, cet apparent paradoxe n'est pas plus valable que le premier car les deux jumeaux n'ont pas des rôles symétriques. Celui qui part dans la fusée n'est plus un observateur inertiel car il subit des accélérations et des décélérations, alors que celui resté sur Terre n'en subit aucune. Il convient d'ailleurs de ne pas oublier que rien n'interdit dans ce raisonnement à la Terre d'être en mouvement de translation uniforme : elle est supposée inertielle, mais pas immobile, ce qui n'a aucun sens dans l'absolu.
Par conséquent, pour faire des calculs valables dans le cadre de la relativité restreinterelativité restreinte, il est nécessaire d'utiliser un système de coordonnées fixe (ou mobilemobile à vitesse constante) par rapport au Terrien, puisqu'il est inertiel. Si l'on souhaitait faire le calcul du point de vue du jumeau voyageur, il faudrait se placer du point de vue d'un observateur non inertiel, cas sur lequel cette théorie ne dit rien (toutefois en relativité généralerelativité générale ce serait possible). Néanmoins, pour obtenir le résultat définitif, la relativité restreinte est suffisante, si l'on prend le soin d'utiliser un système de coordonnées valable.

Compte tenu de la technologie actuelle, l'expérience de Langevin reste impossible à vérifier sur des êtres humains. Cependant, une expérience très similaire a été réalisée à l'aide d'horloges embarquées dans des avions faisant le tour de la Terre en sens contraire avant de revenir à leur point de départpoint de départ (on aurait tout aussi bien pu procéder avec une seule horloge mobile et une horloge fixe à la surface de la Terre). Pour mettre en évidence l'effet attendu, on peut montrer qu'une précision de l'ordre d'une microseconde (un millionième de seconde) est suffisante. Or, les horloges de pointe actuelles sont tout à fait capables d'arriver à une telle précision et l'effet prédit par la relativité restreinte a bien été observé.
Par ailleurs, même si la dilatation temporelle est désormais un effet constaté presque tous les jours dans les accélérateurs de particules, on a pu l'observer avant même la constructionconstruction de ceux-ci grâce aux rayons cosmiquesrayons cosmiques. En effet, il existe un cousin de l'électronélectron, nommé « muonmuon », qui nous parvient parfois de la haute atmosphèreatmosphère à des vitesses très proches de celle de la lumière (voir le dossier sur l'antimatière). Ces muons ont été créés lors de réactions entre les moléculesmolécules atmosphériques et des particules, éjectées au cours d'évènements astrophysiquesastrophysiques extrêmement violents, qui ont parcouru plusieurs années-lumièreannées-lumière avant de nous parvenir. Toutefois, les muons ont une propriété très précisément vérifiée lors d'expériences de physiquephysique des particules faites au sol (et dans lesquelles ils naissent avec des vitesses moindres) qui est leur instabilité : un observateur qui regarde un muon immobile par rapport à lui le voit se désintégrer en deux millionièmes de seconde. Ainsi, cette propriété étant universelle, aucun muon produit dans l'atmosphère ne devrait nous parvenir, cette duréedurée ne permettant pas à une particule, même à la vitesse c, de parcourir cette distance.
Cependant, cette conclusion repose sur une erreur de raisonnement, qui est que la durée de vie du muon mentionnée auparavant est celle dans un système de coordonnées lié au muon, c'est-à-dire son temps propretemps propre de vie. Dans le référentielréférentiel lié au sol, la dilatation temporelle joue son rôle et le muon semble avoir une durée de vie d'autant plus longue qu'il se déplace rapidement. L'observation de muons nés dans l'atmosphère est donc une autre preuve de la « réalité » des effets relativistes. Toutefois, il est important d'insister sur le fait que ces « contractions spatiales » ou « dilatations temporelles » n'ont pas plus de réalité physique que n'en ont les changements de taille qui semblent accompagner le mouvement via les effets de perspective1. Une fois intégrée la nécessité de renoncer au temps et à l'espace absolus et universels (vérifiée expérimentalement chaque jour), les effets prédits par la relativité restreinte ne devraient rien avoir de plus surprenant que ces derniers. Si ce n'est que nous ne les observons pas dans la vie de tous les jours puisque les vitesses relativistes sont peu courantes pour les objets matériels. Malheureusement, il en est de même de la plupart des autres prévisions de cette théorie, qui reste donc souvent incomprise, même si les militaires ont rapidement compris qu'ils pouvaient tirer profit de l'équivalence entre massemasse et énergieénergie.
Observations de l'équivalence entre masse et énergie
Comme cela a déjà été rappelé (voir page précédente de ce dossier), la fameuse équationéquation E = mc² a pour implication première que la masse n'est qu'un type particulier d'énergie, ce qui signifie aussi la possibilité de convertir l'une ou l'autre de ces grandeurs en la deuxième. Ce phénomène est derrière l'énergie libérée par les armes nucléaires, mais il ne faudrait pas oublier qu'il a également des implications bien plus constructives, puisque c'est par exemple « grâce à lui » que brillent les étoilesétoiles et que sont nés les atomesatomes qui nous composent (voir aussi le dossier sur l'énergie nucléaire).
En effet, avant que n'apparaissent les premières étoiles, les seuls atomes qui peuplaient l'universunivers étaient des atomes d'hydrogènehydrogène (l'atome d'hydrogène est le plus léger ; son noyau ne comporte qu'un protonproton) avec, dans une plus faible proportion, des atomes d'héliumhélium, les atomes plus lourds étant négligeables et/ou non existants. Avec le temps, les nuagesnuages stellaires, que formaient ces atomes allaient s'effondrer sous leur propre poids pour donner naissance aux étoiles de la première génération et indirectement aux atomes plus lourds.

En effet, le lent effondrementeffondrement d'un nuage stellaire implique une hausse, lente mais inexorable, de sa température et de sa densité, ce qui permet à des réactions de fusion nucléairefusion nucléaire de s'amorcer2 au cœur de ce qui est devenu une proto-étoileproto-étoile. Ces réactions ont pour effet systématique de former, à partir de plusieurs noyaux, un noyau dont la masse est inférieure à la somme des masses initiales, la différence entre la masse finale et la somme initiale étant nommée « défaut de masse » (voir figure précédente). Ce défaut de masse est converti en énergie, qui est libérée sous forme de rayonnement et d'énergie cinétiqueénergie cinétique microscopique, ce qui crée une pressionpression capable de résister à la gravitationgravitation. Tout au long de son évolution ultérieure, au moins tant qu'elle le peut, l'étoile utilise les réactions nucléairesréactions nucléaires pour produire de l'énergie et résister à la gravitation.
Lorsqu'à la fin de sa vie l'étoile ne peut plus fusionner de noyaux, deux grandes catégories de destins s'offrent à elle, la valeur de la masse initiale de l'étoile étant le principal paramètre régulateur. Si cette masse est trop faible, l'étoile devient stérile une fois tous les carburants possibles épuisés. Dans ce cas, il reste, après diverses péripéties, un cadavre petit (un rayon de l'ordre de celui de la Terre) et dense (la même masse que le soleilsoleil environ, soit un million de fois celle de la Terre), de composition variable (une structure en couches dont l'élément central est le plus lourd d'entre les éléments qui ont été produits), une naine blanchenaine blanche, condamnée à se refroidir lentement. Si la masse initiale de gazgaz est assez importante, les diverses réactions qui se succèdent vont au contraire le faire jusqu'à ce que du ferfer soit produit en grande quantité au cœur de la structure « en pelure d'oignonoignon » de l'étoile. L'élément 56 du fer étant le plus stable, il ne peut plus réagir : la fusion de noyaux de fer 56 ne libère pas d'énergie, elle en consomme. Ce fer s'accumule donc, et, lorsque la masse du cœur dépasse une valeur critique, dite de Chandrasekhar, environ 1,2 fois la masse solaire, le cœur s'effondre brusquement sous l'effet de la gravitation, phénomène qui peut donner naissance soit directement à un trou noirtrou noir, soit à une supernovasupernova gravitationnelle laissant en son centre un trou noir ou une étoile à neutronsétoile à neutrons. Mais le plus important pour nous est que cette explosion aura libéré dans l'espace tous les noyaux atomiques produits au sein de l'étoile (tout en créant les noyaux plus lourds que le fer), lesquels donneront à nouveau des nuages interstellairesnuages interstellaires, et donc des étoiles, qui ne seront cependant plus formées uniquement d'hydrogène. Les éléments les plus lourds de ces nuages permettront ainsi qu'autour des futures étoiles subsistent des « disques nuageux » pouvant eux-mêmes mener à la création de planètes « telluriques » (non gazeuses) telles que la Terre.
On a beaucoup entendu parler du projet IterIter, dont le but est justement d'utiliser ces réactions de fusion pour générer de l'énergie en grande quantité. La raison principale pour laquelle cela n'a jamais été réalisé de manière non militaire est que de telles réactions, tout en nécessitant de grandes énergies3, demandent aussi de très grandes précautions si l'on souhaite éviter qu'elles ne s'emballent et ne libèrent l'énergie de manière explosive. Cela signifie également que militairement, cela a déjà été utilisé depuis longtemps... En revanche, le fait que l'élément 56 du fer soit le plus stable est relié à l'existence d'un autre phénomène qui fait intervenir l'équivalence entre masse et énergie. Il s'agit de la radioactivitéradioactivité (alpha), qui est la fissionfission naturelle d'un noyau plus lourd que le fer en plusieurs noyaux plus petits et telle que la somme des masses de ces noyaux soit inférieure à la masse du noyau initial. Cette réaction libère donc également de l'énergie et peut être utilisée avec « un peu moins » de risques que la fusion dans les centrales nucléairescentrales nucléaires (commentaire très relatif qui ignore le problème des déchets nucléairesdéchets nucléaires).
Dans les réactions décrites précédemment, une partie de la masse mise en jeu était convertie en énergie (principalement sous forme de photonsphotons), cependant il existe également des phénomènes dans lesquels toute la masse mise en jeu disparaît au profit d'énergie sous forme de photons, ou bien d'autres dans lesquels des photons se convertissent en matièrematière. Il s'agit des processus d'annihilation et de matérialisationmatérialisation, le premier se produisant lorsque des particules de matière rencontrent leurs « antiparticulesantiparticules » (voir le dossier sur l'antimatière). Ces processus seront brièvement décrits par la suite, mais ce sera après une présentation de quelques-unes des conséquences qu'eut, au sein de la physique théorique, la relativité restreinte, la prédiction de l'existence de l'antimatièreantimatière étant l'une d'entre elles.
Équation de Dirac et électrodynamique quantique
En 1926, le physicienphysicien autrichien Erwin SchrödingerErwin Schrödinger découvrit l'équation fondamentale de la mécanique quantiquemécanique quantique, qui porteporte désormais son nom. Décrivant la propagation de l'onde de probabilité associée à une particule quantique, cette équation est invariante lors d'un changement de coordonnées galiléen4. Très rapidement, le physicien anglais Paul DiracPaul Dirac se posa donc la question légitime de l'existence d'une équation équivalente pour décrire l'électron, mais qui soit invariante sous les changements de coordonnées de Lorentz. Imposant, pour des raisons techniques, que cette équation d'onde relativiste soit du premier ordre par rapport au temps, Dirac comprit qu'elle devait être « matricielle », portant sur des objets mathématiques à plusieurs composantes. En 1929, il obtint cette équation qui, pour une quantité de mouvementquantité de mouvement donnée, contenait quatre solutions décrivant des particules de même masse, deux d'entre elles ayant cependant une énergie négative. Plus précisément, Dirac en vint à interpréter les deux solutions d'énergie positive comme deux états de « spinspin »5 de l'électron, et les deux d'énergie négative comme deux états de spin d'une particule « jumelle » de l'électron. Traitant le cas avec le champ électromagnétiquechamp électromagnétique, il montra de plus que cette particule jumelle devait avoir une charge électrique opposée à celle de l'électron. Plus étonnant, le résultat de la collision entre un électron et sa particule jumelle devait mener à la disparition de ces deux particules. Grâce à ses arguments avant tout mathématiques, Dirac avait ainsi réussi à prédire l'existence de l'antimatière, via celle du positronpositron, qui fut découvert peu après (en 1932) dans les rayons cosmiques par le physicien américain Carl David Anderson. Cependant, l'interprétation directe de l'équation de Dirac n'était pas des plus claires, le nombre de particules n'étant pas une grandeur conservée dans le contexte relativiste, alors que l'équation de Dirac décrit une particule isolée. Il fallut encore attendre quelques années pour que les ambiguïtés disparaissent dans le cadre de l'électrodynamique quantiqueélectrodynamique quantique, autre théorie reposant sur la relativité restreinte.

Par construction, la théorie de Maxwell de l'électromagnétismeélectromagnétisme était relativiste, et, avec le formalisme quadridimensionnel de Minkowski, on découvrit même qu'elle pouvait s'écrire de manière très condensée. En effet, la densité de charge électrique et le vecteur de flux de densité de charge s'avérèrent former un (quadri)vecteur pour les transformations de Lorentz, alors que les six (2 x 3) composantes des champs électriquechamps électrique et magnétique forment ce que l'on nomme un « tenseurtenseur » antisymétrique6, objet mathématique généralisant le « vecteur » et qui apparaît naturellement dans la théorie de Minkowski.
Cependant, la théorie de Maxwell n'était pas une théorie quantique, et trouver son équivalent quantique n'était pas trivial, étant donné que la mise au point de la physique quantiquephysique quantique n'avait consisté jusqu'alors qu'en la « quantificationquantification » d'équations décrivant des particules isolées, cas bien plus simples que celui d'un champ. En effet, en physique classique, pour décrire la position d'une particule et son état de mouvement, il suffit de connaître six nombres : les trois coordonnées de sa position, et les trois composantes de sa vitesse associées à ces coordonnées. On dit qu'il y a six degrés de liberté. En revanche, la connaissance de l'état physique d'un champ non quantique, tel le champ électromagnétique, passe par celle de la valeur du champ en chaque point de l'espace-tempsespace-temps. Cela implique un nombre infini de valeurs à connaître. Sans même entrer plus dans les détails techniques, on peut imaginer l'ampleur des difficultés techniques et conceptuelles impliquées par la recherche de la version des équations quantiques de Maxwell.

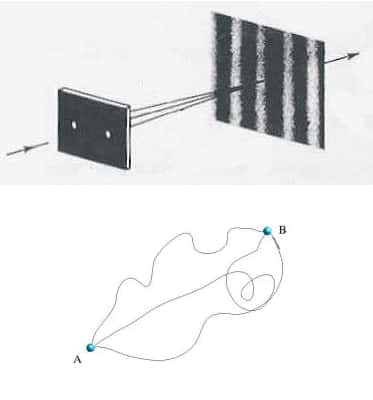
L'électrodynamique quantique ne fut véritablement formulée qu'en 1948, suite aux travaux du Japonais Sin-Itiro Tomonaga et des Américains Julian Schwinger et Richard FeynmanRichard Feynman, chacun d'entre eux découvrant la formulation de cette théorie de manière indépendante. Toutefois, les travaux de Feynman sont les plus connus et furent fondamentaux pour l'émergenceémergence ultérieure d'autres théories telles que la chromodynamique quantiquechromodynamique quantique (qui décrit l'interaction entre les quarksquarks, ces particules qui constituent les neutrons et protons ; voir le dossier sur le plasma de quarks-gluons). En fait, ce que Feynman découvrit est même une reformulation de la physique quantique qui soit « naturellement » relativiste, puisque l'espace-temps de Minkowski est l'ingrédient fondamental. Ainsi, on dit parfois que la mécanique quantique non relativiste peut « se comprendre » en considérant (ce qui reste cependant une manière maladroite et inexacte de formuler la physique quantique) que pour aller d'un point A à un point B, une particule emprunte tous les chemins possibles entre ces deux points, si l'on « n'observe pas » le chemin par lequel elle est passée (un exemple très connu étant celui « des fentes de Young » ; voir la figure suivante). De manière équivalente, la formulation que proposa Feynman de la physique quantique relativiste repose sur le postulatpostulat selon lequel pour déterminer l'état d'une particule en un évènement (x', t') étant donné son état en (x, t), il faut d'une certaine façon considérer que la particule « emprunte »7 tous les chemins possibles joignant ces deux points. Mais les chemins à considérer sont des chemins à travers l'espace-temps et le long de certains d'entre eux, la coordonnée t n'est pas nécessairement croissante. Autrement dit, une particule qui suit cette trajectoire « passe une partie de son temps à remonter le temps », ce qui peut aussi « se comprendre » (depuis Feynman) en considérant que les antiparticules sont « juste des particules qui remontent le temps ».
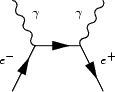
Malgré ces affirmations qui peuvent a priori sembler complètement délirantes, l'électrodynamique quantique offre un cadre théorique fiable dans lequel les phénomènes d'annihilation et de matérialisation sont parfaitement formulés. Ce ne sont que des « changements de forme » de l'énergie, qui n'est plus réellement répartie de manière concentrée entre des particules, mais plutôt de manière continue entre des champs, les particules étant les « effets visibles discrets » de ces derniers. En outre, la formulation de Feynman repose sur des graphes spatio-temporels qu'il découvrit et qui portent désormais son nom. Ces fameux « graphes de Feynman » sont des outils de visualisation et de calcul pour étudier ce genre de phénomènes. Ainsi, sur la figure suivante, l'un de ces graphes est donné en exemple, graphe sur lequel l'une des directions est spatiale et l'autre temporelle, le choix de ces directions étant nécessaire pour identifier le processus physique décrit. Si le temps est horizontal et orienté vers la droite, le graphe représente l'absorptionabsorption d'un photon par un électron qui le réémet peu après. En revanche, si le temps est orienté vers la gauche, il s'agit du même processus, mais pour un positron. Finalement, si le temps est vertical et vers le haut, il s'agit de l'annihilation d'une paire électron/positron donnant naissance à une paire de photons, et inversement, le temps vers le bas correspond à la matérialisation d'une paire de photons sous forme électron-positron.
Ce dernier phénomène, observé pour la première fois en 1933 par les physiciens français Irène Joliot-CurieIrène Joliot-Curie et Frédéric Joliot, est illustré sur la photo suivante, qui est d'ailleurs celle de leur première observation. On y constate l'apparition soudaine de deux particules matérielles de charges électriques opposées, ce qui se traduit, en présence d'un champ magnétiquechamp magnétique, par deux trajectoires de courbures opposées. Depuis cette époque, l'observation de l'antimatière est devenue un phénomène assez banal, même si sa création et son stockage en grandes quantités restent encore très difficiles. Toutefois, les positrons sont quotidiennement utilisés dans l'imagerie médicale par l'intermédiaire de ce que l'on nomme « caméras à positrons ».

Ainsi, bien que pouvant sembler complètement farfelue, la formulation de Feynman de l'électrodynamique quantique, qui est bien plus subtile qu'il n'y paraît, est l'un des outils les plus puissants de la physique moderne actuelle, les prédictions de l'électrodynamique quantique faites grâce à elle étant (selon la phrase de Feynman) « aussi précise(s) que la mesure de la distance Los Angeles-New York à l'épaisseur d'un cheveu près ». Mais, parmi les nombreuses descendantes de la relativité restreinte, ce n'est pourtant pas celle qui a été le mieux validée expérimentalement. En effet, celle pour laquelle l'accord entre la théorie et les mesures expérimentales est le meilleur est un autre sujet : la relativité générale, vérifiée avec une précision d'une partie pour cent mille milliards (1/1014).
Notes :
1 La durée de vie du muon est une grandeur absolue, en ce sens où si l'on prend bien soin de mesurer la durée de vie des muons observés en unités de temps propre, on vérifie qu'ils ont tous la même.
2 On note d'ailleurs que si la masse de gaz n'est pas suffisante (inférieure à 8 % environ de la masse du Soleil), ces réactions ne se déclenchent jamais et l'effondrement ne conduit pas à une étoile mais à une planète ou à une naine brunenaine brune.
3 Car les noyaux ont des charges électriques qui font qu'ils se repoussent initialement avant de pouvoir fusionner s'ils se touchent. On parle de « barrière coulombienne à franchir ».
4 Les modifications apportées par le changement de coordonnées peuvent être incluses dans un facteur de phase de la fonction d'onde, ce qui n'influe pas sur la physique.
5 Une image très grossière pour décrire les deux spins possibles consiste à se représenter l'électron comme une petite flèche ou toupie pouvant tourner sur elle-même de deux façons opposées : la pointe vers le haut ou vers le bas.
6 Un tenseur est une sorte de tableau carré qui, dans le cadre relativiste, est formé de 16 coefficients. Le fait qu'il soit « antisymétrique » signifie que seuls six de ces coefficients sont indépendants. De plus, la décomposition de ce tenseur en champs électrique et magnétique explique naturellement que le premier soit un champ vectoriel et que le second soit pseudo-vectoriel (grossièrement : ils se comportent différemment si on les observe dans un miroirmiroir).
7 Il est évidemment hors de question de formuler ici d'un point de vue mathématique propre les termes utilisés, mais il ne faudrait pas les prendre au pied de la lettre et imaginer des « boules newtoniennes » se déplaçant dans tout l'espace-temps simultanément.