au sommaire
Avec EinsteinEinstein, le temps et l'espace ne sont plus absolus. Dès lors, ils laissent place au concept d'espace-temps, subtile union des deux, proposé par Hermann Minkowski. Sans cette approche, Einstein n'aurait jamais pu formuler sa théorie de la relativité générale.
La relativité restreinte retrouve les formules de transformations de coordonnées que Hendrik Antoon LorentzHendrik Antoon Lorentz avait proposées, avec cependant beaucoup moins d'hypothèses que lui.

Les conséquences immédiates de la relativité
Toutefois, la première grande différence est que, pour Einstein, le temps « local » t' de Lorentz (voir page précédente de ce dossier) n'a rien de mystérieux. Il s'agit tout simplement du temps pour l'observateur attaché au système de coordonnées (x', t'), système tout aussi valable que celui par rapport auquel il est mobilemobile, le système (x, t). Aucun de ces deux temps n'est plus « local » ou moins réel que l'autre.
Par ailleurs, les démonstrations d'Einstein ne font aucunement appel à des effets électromagnétiques ad hoc, et, même si, de ces formules, ressortent toujours les phénomènes de « contraction des longueurs » et de « dilatationdilatation temporelle », ils ne sont plus interprétés comme des « effets physiques » mais plutôt comme des « illusions d'optique », les durées et longueurs n'étant « proprement mesurées » que dans un référentielréférentiel immobile par rapport au système considéré (cette remarque sera justifiée plus tard grâce à la notion de « temps propretemps propre » introduite par Minkowski).
Ainsi, il est assez facile de montrer que si, dans un système de coordonnées, un objet mesure une longueur l, dans un système de coordonnées en mouvementmouvement à la vitessevitesse v par rapport au premier, le même objet ne semblera pas mesurer la même longueur : l'objet mobile paraîtra contracté, dans la direction de son mouvement, d'un facteur 1/γ. De plus, similairement, le temps selon Einstein n'étant plus un absolu, on peut montrer que la durée séparant deux évènements ayant lieu au même endroit n'est plus une grandeur absolue et dépend du système de coordonnées dans lequel on la calcule/mesure. Si la durée est T dans le système par rapport auquel le lieu est fixe, alors, dans le système en mouvement par rapport au premier, la durée mesurée sera supérieure à T, le facteur de dilatation étant γ.
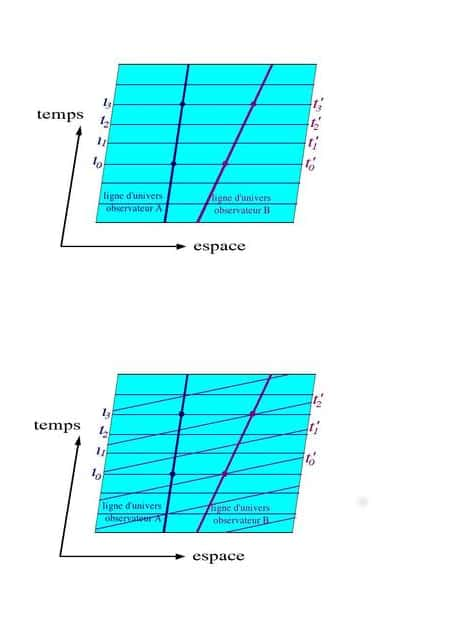
Toutefois, le principe de relativité étant derrière tout cela, il y a une symétrie totale entre les deux systèmes de coordonnées : chacun verra l'autre se contracter spatialement et se dilater temporellement. Ce qui peut sembler au premier abord paradoxal n'est pourtant que la transcriptiontranscription spatio-temporelle d'un problème qui existe déjà en physique newtonienne : le problème d'erreur de la parallaxeparallaxe, qui est une erreur systématique de lecture d'échelle que l'on peut faire en lisant obliquement une graduation. Deux objets (ou systèmes de coordonnées) en mouvement l'un par rapport à l'autre ne sont pas « bien alignés au sens spatio-temporel ».
Cette interprétation ne doit néanmoins pas faire oublier qu'elle n'a été rendue possible qu'en renonçant aux connaissances a priori et au caractère absolu du temps et de l'espace. Elle laisse également entrevoir ce que Minkowski a énoncé : ces deux concepts perdent toute réalité physique, laissant place à celui d'espace-temps, subtile union des deux. Avant d'en venir à l'approche de Minkowski, il reste à détailler dans le cadre de pensée pré-minkowskien, la façon dont se composent les vitesses et son impact sur la causalité.
En effet, il a déjà été dit que la formule de composition des vitesses proposée par GaliléeGalilée est une conséquence des formules de changement de coordonnées déjà mentionnées :
x = x' + vt'
t = t'.
Les formules de Lorentz doivent donc donner une formule de composition des vitesses qui ne soit plus la simple v + w, nouvelle formule qui devra comporter l'invariance de la vitesse de la lumièrevitesse de la lumière c. On peut ainsi montrer que, dans le cadre relativiste, si un objet va à une vitesse v par rapport à un système de coordonnées qui se déplace à la vitesse w par rapport à un autre système, alors la vitesse de l'objet par rapport à ce dernier système ne sera pas w + v, mais :
(w + v)/(1 + wv/c²).
Il est facile de vérifier que si l'une ou l'autre des vitesses w ou v est égale à c, alors le résultat de cette « composition » sera c. L'invariance de la vitesse de la lumière (dans le vide) est donc bien respectée. Par ailleurs, cette même formule explique pourquoi la relativité selon Einstein fut si longue à être découverte : si les deux vitesses sont petites devant c, le deuxième terme du dénominateur devient obsolète et l'on retrouve la formule usuelle d'addition des vitesses. De même, bien que cela n'ait pas été mentionné, il est peut-être utile de signaler que les formules des transformations de Lorentz redonnent bien les formules galiléennes si la vitesse v entre les référentiels est petite devant c : la théorie d'Einstein est équivalente à celle de NewtonNewton pour les petites vitesses, condition nécessaire à sa validité.
Toutefois, on peut montrer que la modification de la formule de composition des vitesses a une implication assez intéressante qui est qu'aucun objet physique usuel (massif) ne peut dépasser la vitesse de la lumière dans le vide, vitesse qui devient une limite infranchissable.
Une bonne compréhension de ce phénomène passe cependant soit par le formalisme minkowskien, soit par le deuxième résultat qu'Einstein publia en 1905 au sujet de sa nouvelle théorie. Restant pour le moment dans le cadre de pensée pré-minkowskien, nous allons considérer ce résultat d'Einstein, qui est aussi l'une des équationséquations les plus célèbres au monde :
E = mc².
L'équivalence entre masse et énergie
Déjà en physique newtonienne, on avait compris que l'énergieénergie n'était pas une grandeur absolue. En effet, une part de celle-ci peut être cinétique, or, la vitesse dépend de l'observateur et il en est donc de même de cette énergie cinétiqueénergie cinétique. Ainsi, il est naturel que, dans le cadre de la relativité selon Einstein, l'énergie soit également relative. Cependant, dans un post-scriptum publié quelques mois après son premier article sur la relativité, Einstein démontra un résultat qui allait faire que sa théorie ne se contenterait pas de révolutionner nos conceptions de l'espace et du temps : elle allait également bouleverser notre façon de percevoir la matièrematière et l'énergie. Ce résultat fondamental était l'équivalence entre la massemasse inertielle et l'énergie, résultat qui allait impliquer que même si elle est en partie relative, l'énergie ne l'est pas complètement.
La démonstration d'Einstein est très courte1 malgré ses implications révolutionnaires. En quelques lignes, exploitant l'invariance de la vitesse de la lumière, Einstein démontre tout simplement qu'un corps qui émet de la lumière voit sa masse inertielle diminuer d'une quantité égale à l'énergie émise divisée par le carré de la vitesse de la lumière. Il aboutit ainsi à sa fameuse équation, qui est d'autant plus riche qu'elle est courte, puisqu'elle n'utilise que les grandeurs physiques « bien connues », que sont la masse et l'énergie, mais implique2 que celles-ci, qui semblaient jusqu'alors différentes, n'en sont qu'une seule. À partir de cette date, les termes techniques restent les mêmes, cependant, les concepts physiques désignés par les mots « masse » et « énergie » ont complètement changé. De plus, comme le principe de conservation ne s'applique plus qu'à l'énergie et non à la masse, on peut aller jusqu'à dire que la masse en tant que grandeur physique fondamentale a disparu : la masse n'est qu'une forme particulière d'énergie.
À ce stade, il est probablement utile d'éclaircir plusieurs points :
- Dans la démonstration d'Einstein, l'énergie à laquelle finit par être égale la masse est l'énergie interne. C'est-à-dire l'énergie de l'objet « mesurée par lui-même » et qui comprend toutes les contributions possibles (thermique, potentielle entre ses constituants, etc.), la contribution cinétique exceptée, car un objet est immobile par rapport à lui-même. Alors qu'en physique newtonienne l'énergie n'avait aucune signification absolue puisque l'on ne mesurait jamais que des différences d'énergie avant et après un phénomène, Einstein démontre donc qu'il existe une échelle absolue pour mesurer l'énergie d'un système, et que la grandeur qui permet de la mesurer est sa masse. On pourrait écrire, dans un premier temps :
U = mc²,
puisque U est généralement la lettre qui sert à désigner l'énergie interne d'un objet.
- Par ailleurs, si l'on exploite l'équation du point de vue d'un observateur qui regarde un objet en mouvement, on peut montrer, avec la même équation, que l'inertieinertie (capacité naturelle des corps à rester dans le même état de mouvement) de l'objet mesurée par cet observateur sera égale à l'énergie divisée par le carré de la vitesse de la lumière. Autrement dit, selon Einstein, l'inertie d'un objet, I, n'est plus égale à sa masse (grandeur qui n'est mesurable que par un observateur fixe par rapport à la masse) mais à son énergie (grandeur qui est relative), et la deuxième information contenue dans l'équation est :
E = Ic².
Bien souvent, on cherche à interpréter l'équation d'Einstein en utilisant simultanément ces deux résultats, et on aboutit alors à des discours selon lesquels la masse d'un objet varie avec sa vitesse. Même si, a priori, ces deux façons de lire l'équation E = mc² peuvent paraître semblables, la formulation de Minkowski et la relativité générale montrent que, pour concevoir les choses proprement, il est mieux de faire cette distinction et de ne pas mettre ensemble les deux lectures de l'équation. La « masse qui varie » n'est qu'un concept trompeur introduit par une lecture newtonienne de la relativité, point qui sera approfondi dans le dossier sur la gravitationgravitation relativiste. Cependant, les conclusions auxquelles nous fait aboutir la théorie d'Einstein peuvent d'ores et déjà se résumer sous forme d'équations :
E = Ic² = U + T = mc² + T,
où T désigne l'énergie cinétique du corps en mouvement.
Le fait d'avoir compris que l'inertie d'un corps dépend de son énergie permet d'appréhender plus aisément le caractère de frontière que joue la vitesse de la lumière. En effet, puisque l'inertie traduit la capacité d'un corps à rester dans le même état de mouvement, plus ce corps a une inertie élevée, plus il faut lui fournir d'énergie pour changer sa vitesse d'une quantité donnée. Jusque-là, rien de nouveau par rapport à la dynamique newtonienne, et ce n'est que la transcription en mots d'un fait quotidiennement observé : il est plus facile de mettre en mouvement une plume qu'une armoire.
Cependant, la nouveauté introduite par la relativité restreinte est le fait que, partant d'un objet ayant une certaine inertie et initialement au repos par rapport à nous, plus nous allons lui fournir d'énergie pour l'accélérer, plus son inertie va augmenter, et plus il faudra lui fournir d'énergie pour l'accélérer. Le résultat qui ressort des équations est sans appel : pour accélérer un objet massif initialement au repos jusqu'à la vitesse de la lumière, il faut lui fournir une énergie infinie. Quand on dit ici « infinie », il ne s'agit pas d'une sorte de métaphore pour dire « très grande et hors de capacité de nos moyens ». Bien souvent, en physique, on considère, par exemple, qu'un système est « infiniment grand » sur le papier, et on constate qu'en pratique cela signifie qu'il est très grand devant le petit morceau qui le compose et sur lequel on se penche précisément. L'infini est une question d'échelle dans ce cas. Or, dans le cas de l'accélération d'un objet dans le cadre relativiste, la seule échelle qui existe est l'échelle de la vitesse de la lumière, et cet infini est donc véritablement infiniment loin et n'a pas le même statut que le premier. C'est un infini de nature qui a un caractère absolu, et qui se comprend d'ailleurs beaucoup mieux dans le cadre de pensée découvert par Minkowski : celui de l'espace-temps quadridimensionnel.

L'espace-temps de Minkowski (la distance spatio-temporelle)
La formulation de la relativité restreinte que proposa en 1908 Minkowski eut peut-être encore plus de difficultés à s'imposer que la formulation initiale d'Einstein. En effet, Einstein lui-même commença par la repousser... La raison en est que, comme Minkowski l'avait annoncé, le temps et l'espace, qu'Einstein avait déjà rendus relatifs, recevaient le statut d'illusions et disparaissaient pour laisser la place à l'espace-temps, concept trop mathématique et abstrait au goût d'Einstein. Toutefois, comme il le reconnut lui-même, Einstein n'aurait jamais pu formuler sa théorie de la relativité générale sans le concept d'espace-temps formalisé par Minkowski.
Dans la brève explication de ce qu'est un système de coordonnées (voir page précédente de ce dossier), il avait été souligné qu'indépendamment du système de coordonnées choisi, certaines grandeurs gardaient des valeurs fixes, et avaient, en quelque sorte, une réalité. C'était le cas, par exemple, de la distance entre deux points, ou, dans le cas du temps, de la durée, ceci dans le cas galiléen. Le succès de Minkowski3 fut de comprendre que, pour la relativité restreinte, l'introduction du temps comme une quatrième coordonnée n'était pas aussi anodine qu'en physique newtonienne. Ainsi, il montra que les apparentes dilatation temporelle et contraction spatiale, qui résultent des transformations de Lorentz, sont uniquement des « erreurs de parallaxe » naturelles pour deux observateurs en mouvement relatif. Plus important, il montra qu'il pouvait affirmer cela car elles cachent l'existence d'une grandeur qui a véritablement une réalité absolue et qu'il découvrit : la distance spatio-temporelle, mélange entre la durée et la distance.
Plus précisément, ce que montra Minkowski est que si on l'envisageait comme un espace géométrique à quatre dimensions, l'ensemble des évènements pouvait être muni d'une notion de (pseudo-)longueur qui soit indépendante du système de coordonnées choisi, si les systèmes retenus sont reliés par les transformations de Lorentz. Étant donné deux évènements ayant, dans un même système, les coordonnées spatio-temporelles respectives (x1, t1) et (x2, t2), la distance spatio-temporelle entre ces deux évènements est :
S² = c²(t2 - t1)² - (x2 - x1)².
Plusieurs remarques sont nécessaires au sujet de cette formule :
- L'écriture adoptée ici ne comporte qu'une seule dimension spatiale afin de simplifier la présentation. Dans le cas général, il faut remplacer le terme « (x2 - x1)² » par le carré de la distance spatiale qui sépare les deux points.
- Dans la description de Minkowski, le quadruplet des coordonnées spatio-temporelles est un « quadrivecteur », de manière analogue à ce qui se passe pour l'espace tridimensionnel euclidien où le triplet formé par les trois coordonnées spatiales est un vecteur. La longueur spatio-temporelle est donc une « pseudo-norme » par analogieanalogie à la norme euclidienne usuelle.
- Une fois obtenue la forme de cette distance spatio-temporelle, on peut réfléchir au problème inverse : quel serait l'ensemble des changements de systèmes de coordonnées qui laissent invariante cette distance ? On montre alors facilement que l'ensemble formé est celui des transformations de Lorentz, auquel on ajoute les translationstranslations d'espace-temps (changements d'origine spatiale et/ou temporelle) et les rotations spatiales4. Cet ensemble, qui a une structure mathématique de groupe, est le groupe de Poincaré. Par ailleurs, on peut, de la même façon, montrer que l'ensemble des changements de coordonnées d'un espace à trois dimensions qui laissent inchangée la distance usuelle de l'espace est l'ensemble des rotations de l'espace et des translations. On parle alors de groupe d'EuclideEuclide, le groupe de Galilée (ensemble qui inclut les transformations de Galilée précédemment mentionnées) étant le groupe obtenu si l'on considère non plus l'espace euclidien, mais l'espace euclidien « muni » d'un temps absolu, en imposant que la distance spatiale et la durée soient invariantes. La conclusion de cette longue digression étant que la mise en applicationapplication du principe de relativité est équivalente à la recherche des invariantsinvariants d'un objet/espace géométrique, ce qui est naturellement lié à l'existence de « lois absolues » gardant les mêmes formes dans tous les systèmes de coordonnées.
- Le membre de droite de cette équation comporte une différence entre deux termes positifs. Le résultat global peut être tout aussi bien positif, nul ou négatif. Toutefois, puisque cet intervalle d'espace-temps est une quantité indépendante du système de coordonnées, le signe ne dépend que des deux évènements. On distinguera les trois cas qui correspondent à trois situations physiques différentes.
- Finalement, on note que cette équation a exactement la même structure mathématique qu'une autre équation clé de la relativité. Il s'agit de celle qui, pour une particule de masse m, d'énergie E et de quantité de mouvementquantité de mouvement p, relie ces trois quantités (définies de manière relativiste) par la relation :
m²c² = (E/c)² - p².
La première caractéristique de cette dernière équation qui vient à l'esprit est que, pour une particule immobile (p = 0), elle redonne exactement la célèbre équivalence entre masse et énergie. C'est donc une généralisation qui illustre une fois de plus la « non-naturalité » de l'introduction d'une masse variant avec la vitesse : m, ici, est une constante. De plus, on peut se convaincre (ou vérifier) que si l'on cherche à exprimer l'énergie et la quantité de mouvement d'une particule pour un observateur étant donné ces grandeurs pour un observateur en mouvement à la vitesse v par rapport au premier, on aboutit à des relations identiques aux transformations de Lorentz. Ceci implique que cette relation entre masse, énergie et quantité de mouvement est valable indépendamment de l'observateur, ce qui n'est pas un hasard, mais une preuve de la structure d'espace vectoriel pseudo-euclidien de l'espace de Minkowski5. Plus précisément, on peut même montrer que cette structure mathématique est à l'origine du fait que la masse d'une particule et la valeur que prend le S² le long de la trajectoire spatio-temporelle (on parle de « ligne d'universunivers ») suivie par celle-ci ne sont pas indépendantes (ce que suggère l'analogie entre les deux équations), comme le montre l'étude de la signification du S² en fonction de ses trois signes possibles.
Pour essayer de comprendre la signification physique de la distance spatio-temporelle, il est utile de commencer par le cas le plus simple, celui où la distance S est nulle. On dit alors que l'intervalle entre les deux évènements est du « genre lumière », pour une raison qui va devenir évidente. Étant donné la définition usuelle de la vitesse (qui n'a pas changé avec la relativité), on voit que cela correspond au cas où les deux évènements sont sur la trajectoire d'une particule se déplaçant à la vitesse c par rapport au système de coordonnées. L'invariance de S est donc équivalente, dans ce cas, à celle de c. Or, il a été mentionné un peu plus haut que, pour une particule donnée, on démontre l'égalité entre le signe de S² le long de sa ligne d'univers et celui de m²c². Autrement dit, les particules qui se déplacent à la vitesse c ont une masse nulle.
Cela permet de relire la vitesse c non plus comme la simple vitesse de la lumière, mais à la fois comme la vitesse limite de l'espace-temps minkowskien, et comme la vitesse de toutes les particules de masse nulle. Plus que la lumière, cette propriété caractérise la structure géométrique de l'espace-temps. Ainsi, une éventuelle mise en évidence d'une masse des photonsphotons n'impliquerait pas nécessairement de devoir abandonner la théorie d'Einstein. Tout au plus, cela changerait les lignes d'univers possibles pour les photons et nous forcerait à parler « d'invariance de la vitesse limite » plutôt que « d'invariance de la vitesse de la lumière dans le vide ». D'ailleurs, il existe déjà des observations qui font que cette seconde appellation est plus justifiée : à l'intérieur de la matière (dans une piscine par exemple), la lumière est fortement ralentie du fait de son interaction avec les particules matérielles, pourtant, la même condition limite s'applique à la vitesse de ces dernières. Si l'on considère d'autres particules non massives, qui n'interagiraient que très peu avec les particules matérielles (par exemple neutrinosneutrinos de masse nulle, s'il y en a, ou bien gravitons), celles-ci continuent à progresser à la vitesse c dans ce même élément de matière, malgré le ralentissement de la lumière.
D'autre part, les lignes d'univers du genre lumière servent à définir des objets géométriques cruciaux en relativité : les cônescônes de lumière. Pour un observateur donné, à chaque instant, le cône de lumière est défini comme l'ensemble des évènements qui peuvent être reliés avec l'évènement « où se trouve l'observateur » par une courbe du genre lumière. Si l'on considère un système de coordonnées dont l'origine (spatio-temporelle) est le lieu où se trouve l'observateur, on voit directement que ce sont tous les évènements qui sont à une distance d de celui-ci et tels que leur date t vérifie :
c²t² = d²,
où d et t varient simultanément. Autrement dit, ce sont tous les évènements qui se situent sur les droites parcourues par les particules de lumière qui sont émises (ou captées si le signe de d et celui de t sont opposés) par l'observateur à l'instant considéré, ce qui justifie l'appellation de « cône » de lumière comme on peut le constater sur les figures suivantes.
Du fait de l'invariance de c, on note de plus que les droites du genre lumière sont invariantes lors d'un changement de coordonnées lorentzien. Ainsi, pour un évènement donné, le cône de lumière, dont cet évènement est le sommet, représente un lieu géométrique défini de manière absolue : il est indépendant de l'état de mouvement de l'observateur.
En physique newtonienne, il y avait pour chaque observateur un même espace et un même temps absolus, en revanche, en relativité restreinte, le temps et l'espace sont différents pour chaque observateur, mais les cônes de lumière sont des objets géométriques absolus qui, en outre, contraignent le mouvement des particules matérielles. En effet, pour un évènement donné, les lignes d'univers qui y passent et qui peuvent être parcourues par des particules matérielles sont toutes celles qui sont situées à l'intérieur du cône de lumière dont l'évènement est le sommet, puisqu'elles sont nécessairement suivies à des vitesses inférieures à c. La surface du cône est quant à elle délimitée par les trajectoires des particules les plus rapides qui soient : celles se déplaçant à la vitesse c.
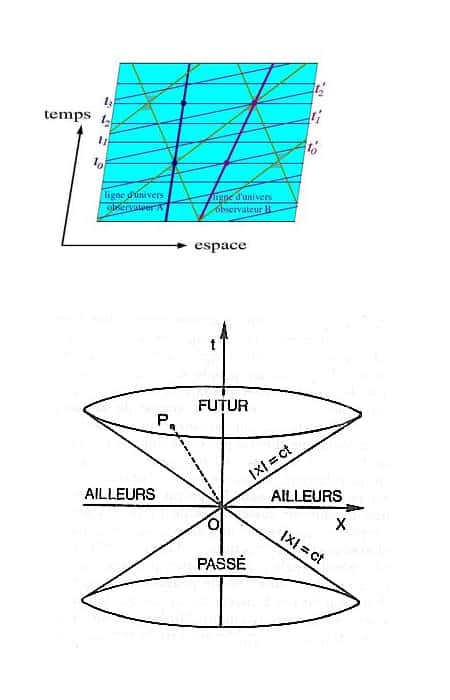
On montre par ailleurs que ces lignes d'univers contenues dans les cônes de lumière sont celles qui sont associées à des valeurs positives de la distance S². En effet, si S² est positive, il existe toujours un observateur (un système de coordonnées) pour lequel la ligne d'univers sépare deux évènements ayant lieu au même endroit, mais à des dates différentes : c'est tout simplement celui qui est « assis » sur la particule de masse m et pour lequel l'équation E = mc² s'applique. On parle donc d'intervalle du « genre temps » pour décrire l'intervalle. On vérifie d'autre part que l'ordre chronologique dans lequel ont eu lieu les évènements reliés par une courbe du genre lumière ou du genre temps est le même pour tous les observateurs inertiels, ce qui est lié à l'invariance des cônes de lumière pour tous les observateurs inertiels. Ceci explique en outre l'emploi des termes « passé » et « futur » sur la figure précédente : à l'intérieur du cône de lumière, ces notions sont définies de manière absolue.
De plus, puisque, pour l'observateur lié à la particule, on peut écrire S² = c²(t2 - t1)² et que S² est une grandeur absolue, indépendante du système de coordonnées, on peut définir le « temps propre » de la particule (ou de l'observateur) comme τ = S/c. Étant donné l'invariance de la distance introduite par Minkowski, le temps propre qui sépare deux évènements donnés, situés sur la ligne d'univers d'une particule matérielle, est donc une grandeur absolue, qui ne dépend pas du système de coordonnées choisi pour la calculer6. Et puisque, pour les observateurs par rapport à qui la particule est mobile, S² comporte également un terme spatial, on remarque que c'est pour l'observateur lié à la particule que la durée qui sépare les deux évènements est la plus courte. C'est pourquoi on observe des « dilatations temporelles » et jamais des « contractions temporelles », les observateurs n'étant pas accrochés aux particules dont ils parlent dans ces situations.
Dans le dernier cas, si S² est négatif, l'intervalle d'espace-temps « sort » du cône de lumière centré sur l'une de ses extrémités, et l'on peut montrer qu'il existe des observateurs pour lesquels les deux évènements qu'il sépare sont simultanés : on parle d'intervalle du « genre espace ». Cependant, la simultanéité n'étant pas un concept absolu, il existera également des observateurs pour lesquels le premier évènement sera antérieur et d'autres pour qui ce sera le second. Dans ce cas, il n'y a pas de chronologie absolue entre les deux évènements, et l'on parle de « l'ailleurs » de l'observateur situé à l'origine pour désigner l'ensemble de ces évènements qui ne sont ni dans son futur ni dans son passé.
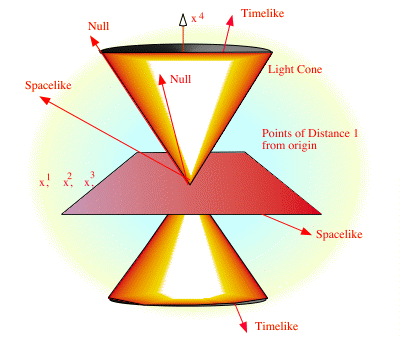
Rassemblant les trois cas possibles, on se retrouve donc dans la situation où si une particule matérielle ou une particule non massive peut joindre deux évènements de l'espace-temps, alors il existe un ordre chronologique inviolable, mais si aucune particule, matérielle ou non, ne peut être « passée » par ces deux évènements (si S² est négatif), aucune chronologie absolue n'existe. Tout ce qui précède amène à formuler le principe de causalité relativiste, qui dit que ne peuvent être liés causalement que deux évènements qui sont séparés par un intervalle du genre lumière ou du genre temps, et que si tel est le cas, la cause précède l'effet quel que soit l'observateur, le signe de cet intervalle étant constant. La vitesse c peut ainsi être interprétée comme la vitesse maximale de la causalité : aucune information ne peut voyager plus vite que c. Et, afin d'insister une dernière fois sur la « puissance » du concept de cône de lumière, on formule « dans leur langage » le principe de causalité en disant que deux évènements sont causalement liés s'ils sont situés dans le cône de lumière l'un de l'autre, ce qui est vrai ou faux indépendamment de l'observateur et du système de coordonnées lorentzien.
Pour conclure cette description théorique de la relativité restreinte, description qui précède celle de ses tests et implications, on peut souligner que certaines personnes ont évidemment essayé d'envisager des particules qui se déplaceraient à une vitesse toujours supérieure à celle de la lumière, c'est-à-dire le long de trajectoires du genre espace. Tentative légitime, puisque ce qui semble interdit par le raisonnement sur l'énergie infinie à fournir semble être de franchir la vitesse de la lumière. Or, pourquoi ne pas considérer des particules qui auraient dès leur création une vitesse supérieure à celle-ci ? Une telle hypothèse semble en effet cohérente : les particules ainsi imaginées (nommées « tachyons ») ont la particularité de se déplacer à une vitesse supérieure à c pour tous les observateurs. Néanmoins, même si la réflexion n'est pas trop problématique dans un cadre pré-minkowskien, elle l'est plus dans le cadre minkowskien car, à cause du lien entre intervalles d'espace-temps et masses des éventuelles particules qui les suivraient, les tachyons devraient avoir des masses dont les carrés seraient négatifs (ce qui reste difficile à interpréter) et pire que ça, ils pourraient voyager instantanément ou bien même remonter le temps, violant ainsi le principe de causalité. Pour ces raisons, on suppose bien souvent que de telles particules n'existent pas, ou bien qu'elles ne peuvent absolument pas interagir avec aucune particule matérielle, ce qui les prive d'une existence « réelle ».
Mais même si les tachyons n'ont jamais été un grand problème pour Einstein (ils sont juste une solution mathématique des équations qui ne semble rien représenter de physique), d'autres problèmes liés à d'éventuelles violations de la causalité relativiste lui donnèrent plus de soucis. En effet, comme Einstein commença à y réfléchir à partir de 1907, si l'on considère la théorie de Newton de la gravitation, il existe une force instantanée et à distance entre deux masses éloignées. Ceci en violation complète des principes de la relativité. Très confiant en la validité de cette dernière, Einstein décida que la gravitation de Newton devait être modifiée, et il pressentit que cela pouvait peut-être se faire en élargissant le cadre de sa théorie, afin que cette dernière rende vraiment général son principe de relativité, auquel les observateurs non inertiels échappaient encore.
Notes :
1 Voir, par exemple, la fin de Einstein 1905, par Balibar, pour une très courte retranscription de cette démonstration.
2 Cela fut vérifié expérimentalement par la suite, l'exemple le plus célèbre ayant eu lieu le 6 août 1945 à Hiroshima.
3 Dans l'un de ses articles de 1905, publié en 1906, Poincaré avait montré le caractère naturel de l'introduction du temps comme une quatrième coordonnée, mais son article resta ignoré, la revue dans laquelle il avait été publié étant trop peu connue.
4 En omettant toutefois les transformations « discrètes » telles que le renversement de la flèche du temps et l'inversion droite-gauche, transformations qui ne sont pas fondamentales ici et compliqueraient inutilement la description.
5 Sans rentrer dans des détails techniques, on peut préciser que cette égalité traduit le fait que le quadruplet mathématique formé de l'énergie et des trois composantes de la quantité de mouvement est un quadrivecteur (vecteur de l'espace quadridimensionnel) dont la (pseudo-)norme est la même pour tous les observateurs : m fois une puissance de c qui dépend de la convention choisie. Ceci est à rapprocher de la remarque précédente selon laquelle l'invariance de S² traduit le fait que le temps et les trois coordonnées spatiales forment un « quadrivecteur position », tout comme ces trois dernières formaient le « vecteur position » euclidien.
6 D'une certaine façon, contre toute attente de la part d'Einstein, on peut dire qu'avec sa formulation de la relativité, Minkowski a réintroduit une sorte de « temps absolu », mais c'est un temps qui est inévitablement local, puisque chaque particule matérielle possède le sien, même si tous les observateurs sont d'accord sur sa mesure.