au sommaire
1905 est un peu une année miraculeuse. C'est l'année de l'élaboration de la théorie de la relativité restreinte par EinsteinEinstein. Découvrez notamment ici comment ce dernier fut influencé par Poincaré et quel est le principe de la relativité selon Einstein.
Rapidement, furent envisagées plusieurs explications des résultats négatifs de l'expérience de Michelson et Morley (voir page précédente de ce dossier). Parmi celles-ci, on peut mentionner l'hypothèse du physicienphysicien irlandais George Francis Fitzgerald, qui supposa que les objets en mouvement subissaient une contraction (d'origine électromagnétique mal comprise) dans le sens de leur mouvement.
Cette idée n'était pas complètement absurde (et peut même sembler naturelle), puisque l'on venait de comprendre que les atomes étaient composés de particules chargées et que leur cohésion était donc d'origine électromagnétique. Elle n'était cependant pas suffisante et fut approfondie par Hendrik Antoon LorentzHendrik Antoon Lorentz, qui montra, à la toute fin du XIXe siècle, que, pour être en accord complet avec les observations, cette contraction des longueurs devait se faire simultanément avec une sorte de « ralentissement du temps ».

Lorentz, les systèmes de coordonnées et le temps
Plus précisément, Lorentz réussit à construire une théorie cohérente qui expliquait tous les résultats expérimentaux connus, mais en utilisant 11 hypothèses indépendantes, dont l'existence d'une sorte de « temps local ».
Pour bien comprendre comment surgit ce temps local, il est nécessaire de considérer d'un peu plus près ce que l'on nomme un « système de coordonnées », qui est un ensemble de nombres, dont le choix n'est pas unique, ayant pour but de permettre de localiser quelque chose dans l'espace.
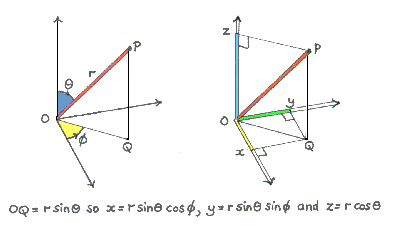
Le monde dans lequel nous évoluons étant en trois dimensions, nous avons besoin de trois nombres, trois « coordonnées », pour nous repérer. Dans une pièce, cela peut être les distances par rapport à deux mursmurs perpendiculaires plus la hauteur par rapport au sol. Le triplet formé de ces trois nombres désigne de manière unique un point de la pièce et permet de calculer la distance entre ce point et celui qui serait désigné par le triplet (0, 0, 0), l'origine du système de coordonnées. De plus, si l'on connaît les coordonnées de deux points différents, on peut calculer la distance séparant ces deux points.
Autre exemple : à proximité de la Terre, nous pouvons utiliser la longitudelongitude, la latitudelatitude et l'altitude1, trois nombres qui permettent de déterminer la distance entre un point et le centre de la Terre (origine de ce système de coordonnées). Notons toutefois que, dans ce cas précis, l'altitude est suffisante pour cela : tous les points à une altitude donnée sont à la même distance du centre de la Terre, indépendamment de leurs latitude et longitude. Cependant, pour calculer la distance entre deux points qui sont à la même altitude, c'est au contraire la longitude et la latitude qu'il faut utiliser parmi ces trois coordonnées, et, dans le cas général, les trois coordonnées sont bien nécessaires.
Le point crucial, déjà mentionné, est que le système de coordonnées choisi est complètement arbitraire, tous étant équivalents, mais tous permettant de calculer les grandeurs qui ont, en quelque sorte, une « existence absolue » (puisqu'elles sont indépendantes du système choisi), la distance entre deux points donnés, par exemple.
Reste maintenant qu'en physique, on cherche à repérer non pas de simples positions dans l'espace, mais plutôt ce que l'on appelle des « évènements ». Un évènement est quelque chose qui a lieu quelque part à un instant donné : la naissance d'un enfant, la désintégration d'un atome, etc. Un évènement (au sens physique) peut toutefois également correspondre à une sorte d'absence d'évènements (au sens usuel) : un objet ponctuel immobile occupera successivement, dans un système de coordonnées donné, tous les évènements indicés par (x0, t), où x0 est sa position et t la date qui varie. On peut donc repérer dans un système de coordonnées spatio-temporel un évènement à l'aide des coordonnées spatiales du lieu où il s'est produit et de la date à laquelle il s'est produit.
La date est ainsi une « coordonnée temporelle », qui remplit bien le même rôle qu'une coordonnée spatiale, car elle permet non seulement de repérer un évènement dans le temps, mais aussi de calculer la « distance temporelle », nommée plus communément « durée », qui sépare deux évènements.
Avant que ne naisse la relativité selon Einstein, ces deux distances n'avaient cependant aucune raison d'être liées, aucune structure de mesure (on parlera de « structure métrique ») ne les connectant. La situation changea complètement avec la relativité einsteinienne, puisque, comme on le verra plus tard, elle démontra que la séparationséparation entre espace et temps n'était pas définie de manière absolue, et que leur union était non seulement possible, mais nécessaire.
Par ailleurs, même si, que ce soit pour les distances ou pour les durées, le système de coordonnées utilisé et son origine n'ont aucune influence sur les mesures (chacun d'entre nous garde le même âge quel que soit le calendrier employé pour le calculer), il reste cependant utile de savoir passer d'un système de coordonnées à un autre pour pouvoir communiquer avec des personnes utilisant un système différent du nôtre. Cela vaut aussi bien pour le temps (décalage horaire par exemple) que pour l'espace (par exemple, calcul de la distance entre deux villes connaissant la distance entre chacune d'entre elles et une troisième). Or, puisqu'en physique on mesure des objets physiques et que le temps est entré dans le jeu, il reste deux choses à prendre en compte :
- Un système de coordonnées spatiales sera souvent « attaché » à un objet physique et on parlera alors du « référentielréférentiel » lié à l'objet ou à l'observateur. La différence entre référentiel et systèmes de coordonnées, très importante d'un point de vue technique, sera ignorée ici où elle serait une complication inutile.
- Il devient nécessaire de savoir également obtenir les coordonnées d'un évènement dans un système de coordonnées spatio-temporel, connaissant ses coordonnées dans un autre système mobilemobile par rapport au premier. Ce problème avait été esquivé, mais il est en fait derrière l'obtention de la formule de composition des vitessesvitesses de GaliléeGalilée.
Pour essayer de comprendre ce qui se passe dans ce dernier cas, on peut se contenter de considérer un « problème unidimensionnel », c'est-à-dire deux axes parallèles mobiles l'un par rapport à l'autre.
L'exemple d'Einstein : celui du train et du quai
L'un des exemples préférés d'Einstein mettait en jeu un train et un quai. La même situation sera donc reprise ici. Dire qu'à l'instant initial l'arrière du train (noté O' et qui servira d'origine pour repérer les positions dans le train) se trouve à l'extrémité arrière du quai (notée O et qui servira d'origine pour repérer les positions sur le quai) signifie qu'initialement, l'arrière du train a pour coordonnée 0 (zéro) dans le système attaché au quai.
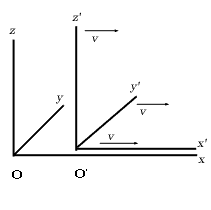
Si le train avance à une vitesse constante v, la distance qu'il aura parcourue au bout d'une durée T sera donc vT. Autrement dit, dans le système lié au quai, l'arrière du train avait initialement comme coordonnées (x = 0, t = 0), puis il a pour coordonnées (x = vT, t = T). Si l'on considère maintenant un voyageur qui se trouvait initialement à l'arrière du train et qui avance à une vitesse w constante dans ce dernier, au bout de la même durée, il aura parcouru une distance wT dans le train.
Cela signifie que, dans le système lié au train, on pourra le repérer par (x' = wT, t = T) et dans celui lié au quai (x = (w+v)T, t = T) puisqu'il aura parcouru la distance vT + wT par rapport au quai : comme cela avait déjà été mentionné précédemment, le voyageur se déplace à la vitesse w + v par rapport au quai. De manière générale, étant donné un évènement de coordonnées (x, t) dans un premier système et (x', t') dans un second système mobile à la vitesse v par rapport au premier, on peut écrire pour relier ces coordonnées :
x = x' + v t'
t = t'
où l'on a artificiellement introduit un temps t' pour munir chacun des systèmes de son propre temps, bien que la seconde égalité traduise l'universalité de ce temps.
Avant d'aller plus loin, quelques remarques sur ces résultats sont nécessaires :
- Si l'on regarde la distance qui sépare le voyageur de l'arrière du train à l'instant final, on trouvera wT, que l'on fasse ce calcul avec le système de coordonnées lié au train (d' = wT - 0) ou celui lié au quai d = (w+v)T - vT : la distance est bien une grandeur absolue.
- Pour faire ce raisonnement, on a implicitement supposé l'existence d'un temps universel absolu, sur les mesures duquel un observateur lié au train et un autre lié au quai seraient d'accord : les durées sont elles aussi des grandeurs absolues.
Si l'on remplace le train par la Terre, le quai par l'étheréther et le voyageur par la lumièrelumière, on peut appliquer ce raisonnement pour en déduire ce qui avait été précédemment dit : la vitesse de la lumièrevitesse de la lumière étant fixée (par les équations de Maxwelléquations de Maxwell) à la valeur c par rapport à l'éther, si la Terre était mobile par rapport à ce dernier, la vitesse de la lumière par rapport à la Terre varierait.
Puisque les expériences très minutieuses de Michelson et Morley n'avaient rien mesuré, il devait y avoir une erreur dans le raisonnement précédent appliqué à la lumière, et c'est comme cela que Lorentz, se reposant sur l'idée de Fitzgerald, en vint à proposer de modifier les formules précédemment obtenues. Il montra ainsi que si l'on suppose que l'on a les transformations, qui portent désormais son nom, alors :
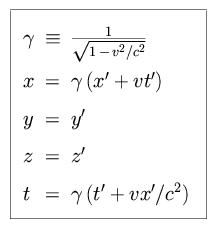
Où le facteur γ (gamma), qui dépend de la vitesse v et de celle de la lumière c, tend vers 1 lorsque v est très petite devant c, alors que cette dernière reste la même quel que soit le référentiel utilisé pour la calculer. Toutefois, il fallait pour cela introduire un « temps local » t' qui restait bien mystérieux.
L'influence d'Henri Poincaré sur Einstein
Par ailleurs, bien que parvenant à rendre compte des résultats expérimentaux, la solution de Lorentz n'était pas vraiment plaisante conceptuellement, le mathématicienmathématicien français Henri PoincaréHenri Poincaré allant même jusqu'à parler de « complot de la nature » pour la décrire avec ses onze hypothèses ad hoc que personne ne comprenait vraiment. D'ailleurs, Lorentz était bien d'accord avec lui sur le fait que trouver quelques hypothèses fondamentales, plutôt qu'une collection d'effets électromagnétiques, serait bien plus satisfaisant pour expliquer les observations. C'est exactement ce que fit Einstein en 1905. Mais, avant d'en venir à lui, il serait injuste de ne pas rendre hommage au travail de Poincaré, dont l'influence sur ce premier fut probablement de très grande importance, certains allant même jusqu'à accuser Einstein d'avoir volé ou plagié Poincaré.
À la fin du XIXe siècle, Poincaré, âgé d'une cinquantaine d'années, était depuis bien longtemps un mathématicien reconnu. Ses domaines d'intérêt n'étant pas cloisonnés aux seules mathématiques ; il avait également contribué à la physique mathématique et s'intéressait aux problèmes soulevés par l'électrodynamique bien avant qu'Einstein, né en 1879, ne soit en âge de le faire. Son esprit critique l'avait par exemple amené à mettre en doute le caractère absolu de la notion de « simultanéité » (comme le fera Einstein) et il était même l'inventeur du terme « relativité » pour désigner le principe de Galilée.
Par ailleurs, Poincaré publia en 1902 La Science et l'Hypothèse, ouvrage de réflexion sur les rapports entre géométrie et physique. Poincaré y exprime explicitement le fait que les notions de temps et d'espace absolus ne sont pas démontrables en ce qui concerne l'espace physique. Il va même jusqu'à affirmer que le caractère euclidien de l'espace n'est qu'un choix « arbitraire »2. Chacune de ces réflexions préfigure la théorie d'Einstein, et, étant donné que ce dernier lut effectivement ce livre de Poincaré avant d'écrire les articles fondateurs de sa théorie de la relativité, le doute semble permis.
Toutefois, les principaux articles de Poincaré sur ce sujet seront publiés à la même période que ceux d'Einstein, ce qui fait que celui-ci ne put vraisemblablement pas les lire avant d'écrire les siens. De plus, même si les articles de Poincaré contiennent des débuts de réflexion concernant des sujets sur lesquels Einstein ne se penchera pas avant quelques années (la gravitationgravitation relativiste par exemple), la démarche d'Einstein sera totalement différente de celle de Poincaré pour énoncer sa théorie de la relativité. En effet, Poincaré restera fidèle à l'idée de Lorentz selon laquelle contraction spatiale et dilatationdilatation temporelle sont des réalités physiques (électromagnétiques), tout en voyant dans la relativité plutôt une « possibilité mathématique »3, et il n'osera pas renier l'existence de l'éther ni celle d'un temps absolu (qui est toutefois, selon lui, une variable inévitablement cachée).
De son côté, Einstein saura retrouver la théorie de Lorentz à l'aide de principes simples, et comme le décrit très bien le livre Einstein 1905 : De l'éther aux quanta, de Balibar, sa théorie de la relativité se positionnait dans une profonde réflexion sur l'opposition continu-discontinu, sur le rôle de l'éther et sur la nature de la lumière, réflexions communes à presque tous les articles qu'il publia en 19054.
Relativité einsteinienne : la simultanéité, un concept relatif selon Einstein
La relativité selon Einstein naît grossièrement de la constatation suivante : l'électromagnétismeélectromagnétisme de Maxwell est une théorie très cohérente, qui marche parfaitement, mais qui semble « asymétriqueasymétrique » si on la joint à la cinématique newtonienne. En effet, du fait de la présence d'un référentiel privilégié lié à l'éther, une expérience dans laquelle un aimantaimant et un conducteur sont en mouvement relatif l'un par rapport à l'autre ne se décrit pas de la même façon si c'est l'aimant ou le conducteur qui est en mouvement par rapport à l'éther. Dans un cas, on parle de champ magnétiquechamp magnétique, et dans l'autre, de champ électriquechamp électrique, malgré des résultats de mesure identiques.
La théorie fonctionne donc correctement pour ce qui concerne le calcul des effets électromagnétiques, ce qui est son but premier, et ce n'est que lorsque l'on cherche à y mettre de la cinématique newtonienne pour « interpréter les observations » ou bien pour mettre en évidence des variations de la vitesse de la lumière, que des problèmes surgissent. Or, comme l'avait très bien compris Einstein, l'éther, en tant que support matériel de la lumière, n'avait que très peu de raisons d'exister, puisqu'il était dénué de toute propriété mécanique, si ce n'est l'immobilité absolue5. De plus, même si la cinématique newtonienne n'avait jamais été mise en défaut, elle reposait sur bien plus d'hypothèses ad hoc que la théorie de Maxwell, qui ne postulait, par exemple, pas l'existence de grandeurs absolues.
Persuadé du caractère simple des lois de la physique, Einstein commence donc sa théorie de 1905 par une remise en cause de bien des évidences liées à la cinématique newtonienne (existence d'un espace absolu, d'un temps absolu, etc.), à commencer par le caractère absolu de la notion de simultanéité. En effet, dire que deux évènements éloignés d'un observateur sont simultanés ne peut avoir qu'une seule signification pour celui-ci : il a vu au même instant ces évènements se produire. Toutefois, si l'on considère un deuxième observateur, mobile par rapport au premier et se dirigeant vers l'endroit où a lieu l'un de ces évènements, la lumière voyageant à une vitesse finie, celle qui provient de l'endroit vers lequel il se dirige lui parviendra la première. Cela signifie que, pour ce deuxième observateur, les deux évènements ne sembleront pas simultanés.
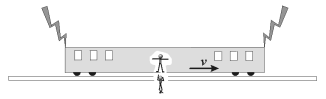
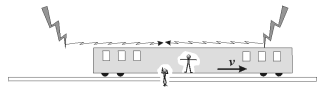
La simultanéité ne peut donc pas être un concept absolu, valable pour tous. Or, si l'on y pense bien, à un instant donné, l'espace est, par définition, l'ensemble des évènements qui semblent simultanés, car l'espace que nous percevons n'est pas un ensemble de points géométriques (qui n'ont pas de réalité physique), mais bien un ensemble d'évènements (x, t) tous décrits par le même temps t. Ainsi, si la simultanéité n'est pas un concept absolu, il ne peut donc pas y avoir d'espace absolu, ni de temps absolu, et pas plus de repos absolu pour l'éther, en tout cas dans le cadre de la cinématique newtonienne. L'éther dénué de sa dernière « propriété mécanique » n'a plus lieu d'être. Seul doit subsister le « champ électromagnétiquechamp électromagnétique » tel qu'il est conçu encore aujourd'hui : un milieu continu omniprésent sans support matériel.
Débarrassé de tous les a priori possibles, Einstein peut ensuite poser sa théorie qui doit également remplacer la cinématique newtonienne. Cependant, bien qu'il renie celle-ci, Einstein tient à garder un principe qu'elle contient et qui lui semble bien plus important que le reste. En effet, son raisonnement l'a conduit à rejeter toute notion d'absolu pour l'espace et le temps. Cela signifie inévitablement que ce sont des grandeurs « relatives » et semble indiquer que le principe de relativité est une sorte de « super-principe ». Or, la version galiléenne épurée de ce principe stipule que les lois de la mécanique sont les mêmes pour tous les observateurs inertiels. Rapprochant ceci de la constatation expérimentale de la constance de la vitesse de la lumière, le raisonnement d'Einstein semble inévitable : le principe de relativité est un principe plus fondamental que toute la cinématique newtonienne. Formulé comme un « principe d'absolutisme » qui affirme que les lois de la mécanique sont les mêmes pour tous les observateurs inertiels, il doit être élargi pour inclure l'électromagnétisme et la valeur de la vitesse de la lumière dans le vide, étant donné que l'éther n'existe pas et que le champ électromagnétique est son propre support.
Le principe de relativité selon Einstein
Ainsi, s'énonce alors le principe de relativité selon Einstein : les lois de la physique, l'électromagnétisme inclus, sont les mêmes pour tous les observateurs inertiels et il en est donc de même de la vitesse de la lumière dans le vide.
Par ces simples postulatspostulats, Einstein parvint à reconstruire toute une cinématique, et même une dynamique, qui, comme la mécanique newtoniennemécanique newtonienne, vérifie le principe de relativité. Par constructionconstruction, cette dynamique a l'avantage, par rapport à la théorie de NewtonNewton, d'être également compatible avec l'électromagnétisme selon Maxwell et de ne plus utiliser la notion d'action à distance instantanée qui embarrassait tant Newton : la force de CoulombCoulomb est devenue un effet, à la limite statique, des équations de Maxwell et résulte donc, tout comme la lumière, de l'existence du champ électromagnétique.
Plus important, cette théorie montra rapidement qu'elle était vérifiée expérimentalement, même si, ayant profondément modifié les notions apparemment évidentes d'espace et de temps, elle ne s'imposa pas du jour au lendemain. En effet, de pseudo-paradoxes peuvent surgir assez facilement, pour qui reste accroché aux conceptions newtoniennes, consciemment ou non. Cependant, peu après sa formulation par Einstein, la relativité « restreinte » (car elle ne traite que des observateurs inertiels) fut dotée, par le mathématicien balte Hermann Minkowski, du formalisme naturel qui lui correspondait et qui reste employé encore aujourd'hui. Comme ce dernier le dit lui-même en 1908, lors de la conférence au cours de laquelle il présenta ses travaux : « Désormais, l'espace en soi et le temps en soi ne sont plus que des ombres vaines et seule une sorte d'union des deux préservera une réalité indépendante ». L'espace-tempsespace-temps de Minkowski était né.
Notes :
1 Et, bien évidemment, à la surface de la Terre, une surface étant en deux dimensions, seules la longitude et la latitude sont nécessaires.
2 Poincaré affirme cependant un peu plus loin, dans le même livre, que « la géométrie euclidienne n'a rien à craindre d'expériences nouvelles ». Voir le livre d'Eisenstaedt.
3 Poincaré est également à l'origine de l'appellation « transformations de Lorentz », et l'aspect avant tout mathématique de son point de vue transparaît dans le fait qu'il démontra que ces transformations formaient un groupe, qu'il élargit d'ailleurs en y ajoutant les translationstranslations d'espace-temps, donnant naissance au « groupe de Poincaré ».
4 1905 fut pour Einstein une année remarquable, étant donné qu'il ne se contenta pas de formuler sa théorie de la relativité restreinte, mais proposa également, démonstration à l'appui, l'existence du photonphoton, et publia un article très important pour la mécanique statistique, ainsi qu'un autre où il démontrait que le mouvement brownien était la trace de l'existence des moléculesmolécules.
5 Il semble qu'Einstein ignorait complètement l'existence des expériences de Michelson et Morley, même s'il avait eu connaissance de l'impossibilité de mettre en évidence le mouvement de la Terre par rapport à l'éther.