au sommaire
La création sous ses multiples aspects procède du nombre d'or. Il s'attribue une quantité de propriétés exclusives et engendre une suite géométrique qui intervient dans toutes les proportions des formes et des nombres.

On connaît maintenant la suite de Fibonaccisuite de Fibonacci, jouons à présent avec une autre suite : la suite géométrique.
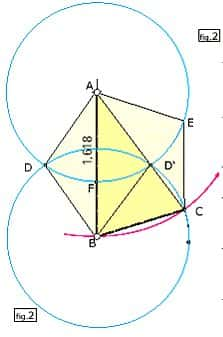
Troisième jeu : une suite connue mais particulière
Reprendre la figure 2 de la page précédente d'où l'on a extrait le triangle sublime ABC que nous voyons ci-dessous en figure 1 et figure 2 avec le triangle sublime BFC (en rose) ayant sa base sur AB et son sommet en C.
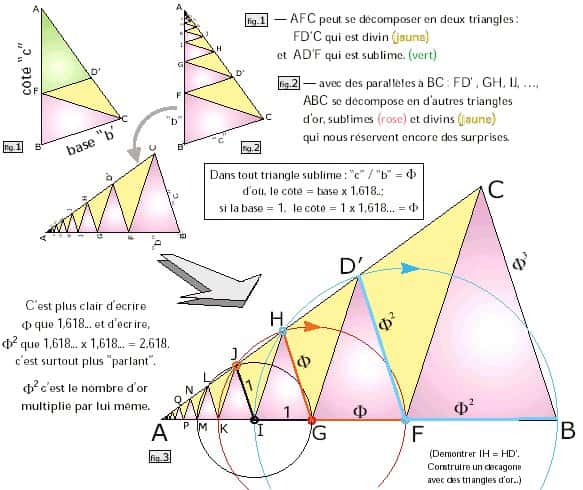
Que remarque-t-on dans cette figure 3 (que l'on peut réaliser à la ficelle, sans aucun calcul) ?
Prenons par exemple IG comme base = 1.
Si IG = 1 alors GH = Φ et GF = GH, rayons du cercle (rouge) de centre G. Il suffit de regarder les triangles sublimes et leurs cercles pour admettre ces égalités.
GF = Φ donc FD' = Φ x Φ = Φ2 et dans le triangle FCB, BC = Φ2 x Φ = Φ3, etc.
Les cercles suffisent pour affirmer que c'est une suite de Fibonacci, mais en plus c'est une suite pour laquelle il suffit de multiplier une longueur par Φ pour avoir la suivante. Une telle suite est appelée une suite géométrique (en effet sur AB, toute base du triangle sublime est égale à la somme des deux bases précédentes), Φ en est la raison et 1 le chiffre de départ.
Le nombre d'or engendre une suite géométrique
Le nombre d'or est le seul nombre à pouvoir engendrer (en plus sans calcul !)) une suite géométrique dont on puisse calculer les termes par additions (ce qui était un avantage avec des chiffres romains !).