au sommaire
Le jeu cryptologique comprend un adversaire avec qui il faut compter. Son but est le décryptement des messages, c'est-à-dire un déchiffrementdéchiffrement sans la clé. Ce travail délicat est essentiel pour assurer la solidité d'un procédé. Comme l'avait déjà fait remarquer Charles Babbage dans un échange du Journal of the Society of Arts, on ne peut proposer un chiffre sûr que si l'on a soi-même décrypté des chiffres très difficiles.

Il est admis aujourd'hui que les substitutions simples tombent rapidement sous les coups de l'analyse des fréquences. La technique utilisée a été exposée pour la première fois par le philosophe et mathématicien arabe Al-Kindi dans son traité sur l'extraction de l'obscur dès le IXe siècle. Le travail de décryptement comprend deux phases :
- l'une, quantitative, consiste à compter les occurrences de chaque caractère dans le texte dont on veut retrouver le sens ;
- la seconde, qualitative, consiste à utiliser la connaissance de la langue et l'intuition.

Le scarabée d'or, une nouvelle d'Edgar Poe parue en 1843, décrit en détail le patient travail du décrypteur. La méthode suit presque mot pour mot un article de David A. Conradus, Cryptographia Denudata, paru en 1842 dans le Gentleman's Magazine.
Charles Babbage, Friedrich Kasiski et leurs méthodes de décryptement
Les substitutions polyalphabétiques ont résisté plus longtemps à l'analyse. Il a fallu attendre le XIXe siècle avec les travaux de Charles Babbage, puis de Friedrich Kasiski pour voir apparaître une méthode analytique de décryptement. L'étape cruciale est la détermination de la longueur de la clélongueur de la clé. Elle est déterminée en repérant les répétitions dans le cryptogramme. Cette méthode a été affinée par William Friedman au début du XXe siècle qui a utilisé l'index de coïncidence, défini comme la probabilité de collision d'un symbole dans le cryptogramme. Cette grandeur, significative de l'information portée par les lettres d'un texte, est connue aujourd'hui sous le nom d'« entropie de Rényi ». Elle permet de distinguer les caractères issus d'une langue naturelle d'une suite purement aléatoire.
L'adversaire est supposé toujours connaître le détail du procédé de chiffrement. Ce principe a été énoncé par le linguiste Auguste Kerckhoffs en 1882, qui prônait des méthodes ne devant pas reposer sur le secret du procédé, mais seulement sur celui d'une clé facilement modifiable. Sa thèse repose sur le principe que Jean-Robert du Carlet a apposé comme devise en tête de son ouvrage sur la cryptographiecryptographie : Ars ipsi secreta magistro, « un art caché au maître lui-même », ce qui signifie qu'un chiffre n'est bon pour autant qu'il reste indéchiffrable par son propre inventeur.

Outre la connaissance du procédé, le jeu cryptologique fournit aujourd'hui à l'adversaire un dispositif qui réalise l'opération de déchiffrement. Il peut l'observer, effectuer des mesures physiques, provoquer des erreurs de fonctionnement, afin d'en extraire les secrets. Il serait en effet indésirable qu'un lecteur de carte bancaire puisse en tirer les secrets, simplement par l'observation de sa consommation électrique, ou du temps passé aux calculs.
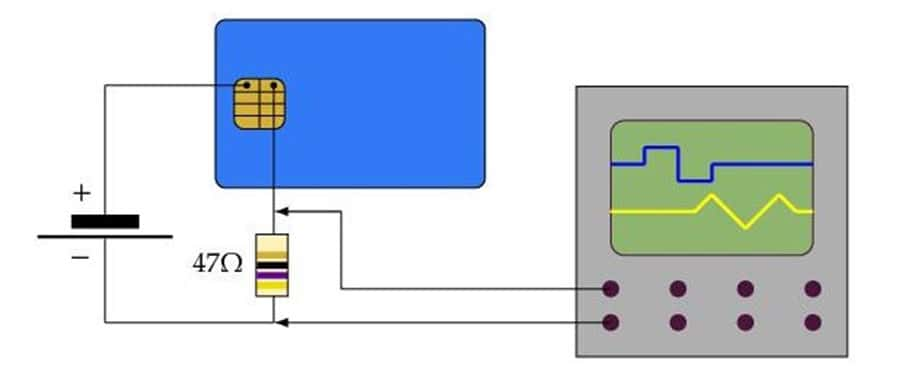
Par exemple, l'observation de la consommation d'une carte à pucecarte à puce peut révéler l'exposant privé utilisé pour un déchiffrement RSA. Fort heureusement, les fabricants de cartes ont su trouver des parades pour résister à ces attaques.