au sommaire
Le problème de la transmission d'un maximum de messages au moindre coût a suscité la recherche, il y a quelques décennies, d'une théorie mathématique de l'information et de la communication.
Bien que déjà entrevue par Hartley R.W., Nyquist H., EinsteinEinstein A., (Moles A., 1971) (Escarpit R., 1976), elle ne fut nettement formulée qu'en 1948 par Shannon C.E. (Weaver W. et Shannon C.E., 1975). Elle suppose :
- d'une part l'existence d'une chaîne de communication dont les constituants sont bien connus : émetteur, canal, récepteur, etc. ;
- d'autre part la transformation par cette chaîne de la forme du message et non de son contenu.
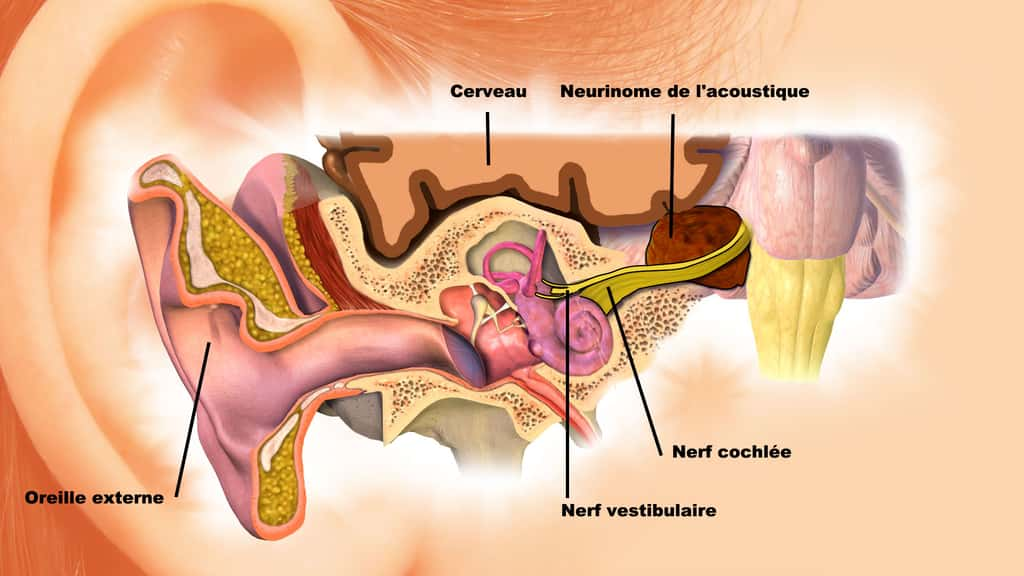
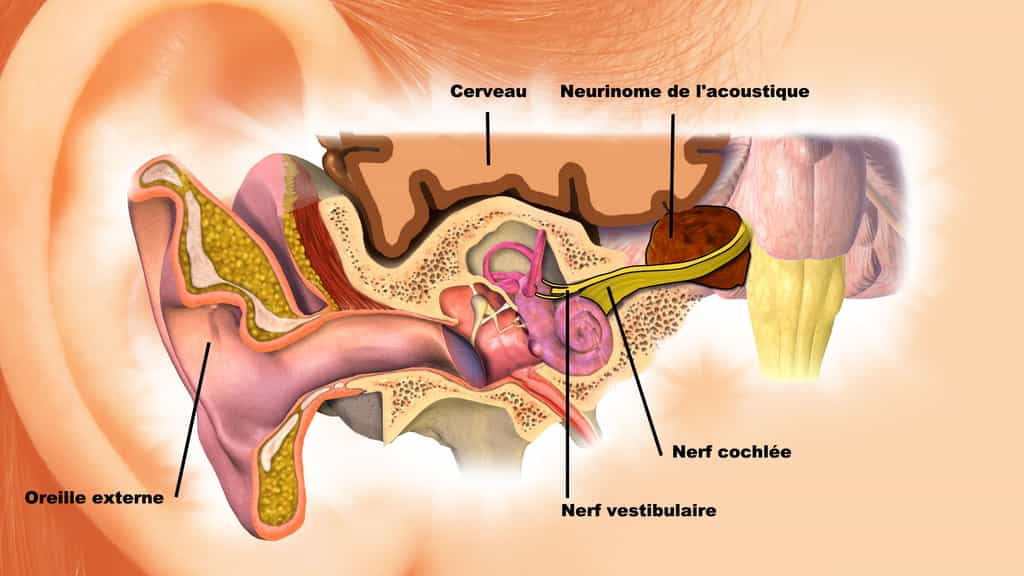
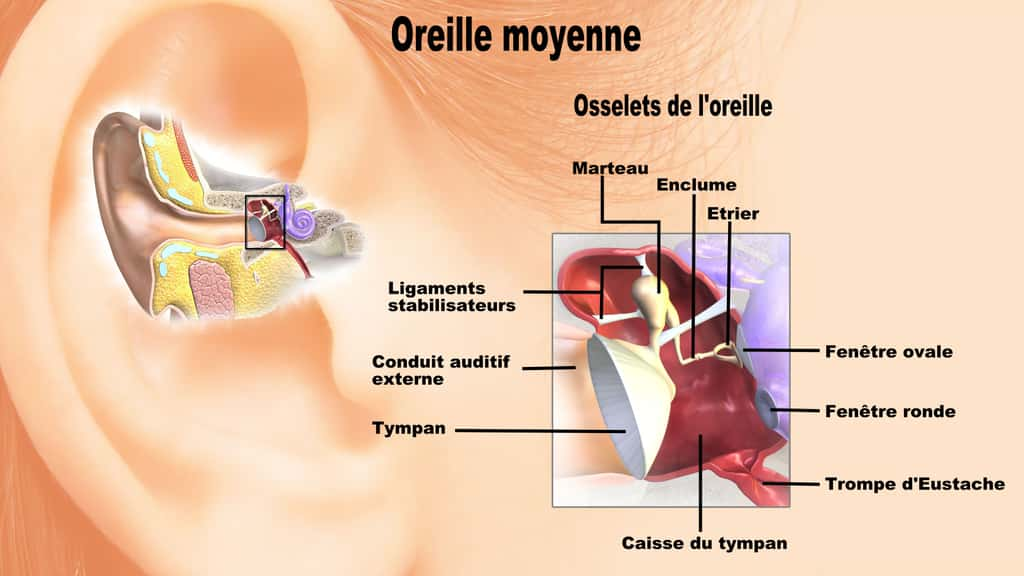
© BruceBlaus, CC BY 3.0
L'essentiel est de réduire le message en une combinaison de signaux 0 ou 1 (tout ou rien, on or off)). La valeur de ce message dépend de l'imprévisibilité relative des combinaisons successives de 0 ou 1 (Moles A.1971) [45, 22].
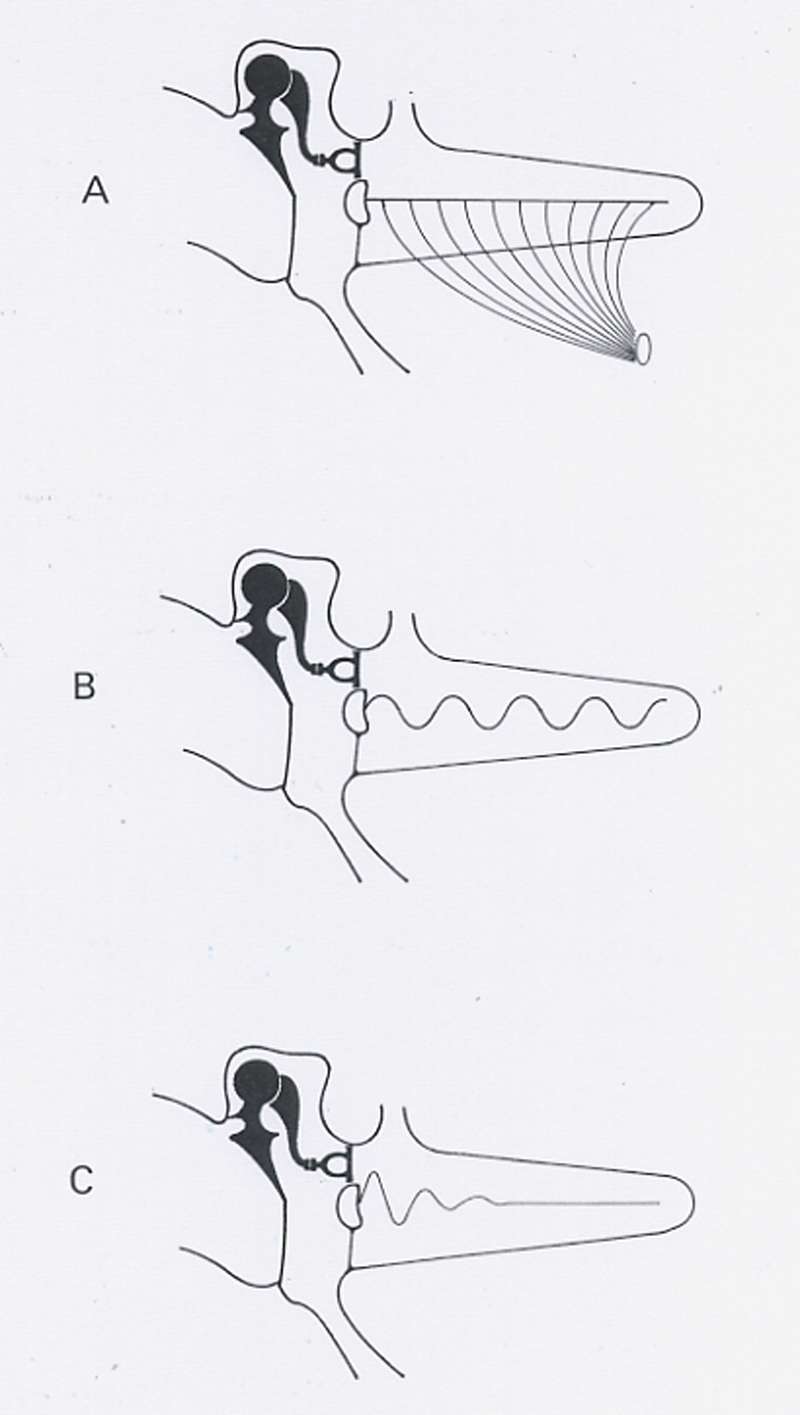
En outre, en élargissant sa portée à celle du signal continu, la théorie montre que ce dernier peut être réduit à un système discret constitué d'un certain nombre de signaux discontinus susceptibles d'être distingués et analysés.
En d'autres termes, tout signal continu peut être représenté de manière significative par prélèvement d'éléments discrets ou échantillons, à intervalles de temps réguliers, à la condition que la cadence d'échantillonnageéchantillonnage soit égale ou supérieure au double de la fréquence maximum du signal.
C'est le théorème de l'échantillonnage - temporel - de Shannon, théorème qui peut être également transposé à l'échantillonnage spatial d'une forme.