Un ballon de football n’est pas une sphère parfaite et c'est cela qui permet de jouer avec des effets. Quels secrets mathématiques se cachent derrière le ballon de foot ? Qu'est-ce que l'effet Magnus qui permet de créer des effets étonnants sur la trajectoire du ballon ? Explications.
au sommaire
Le gonflage du ballon de football le fait ressembler à une sphère. Pour être une bonne approximation de la sphère, a priori l'idéal aurait été d'utiliser un polyèdre régulier au plus grand nombre de faces possible, c'est-à-dire l'icosaèdre qui a vingt faces.
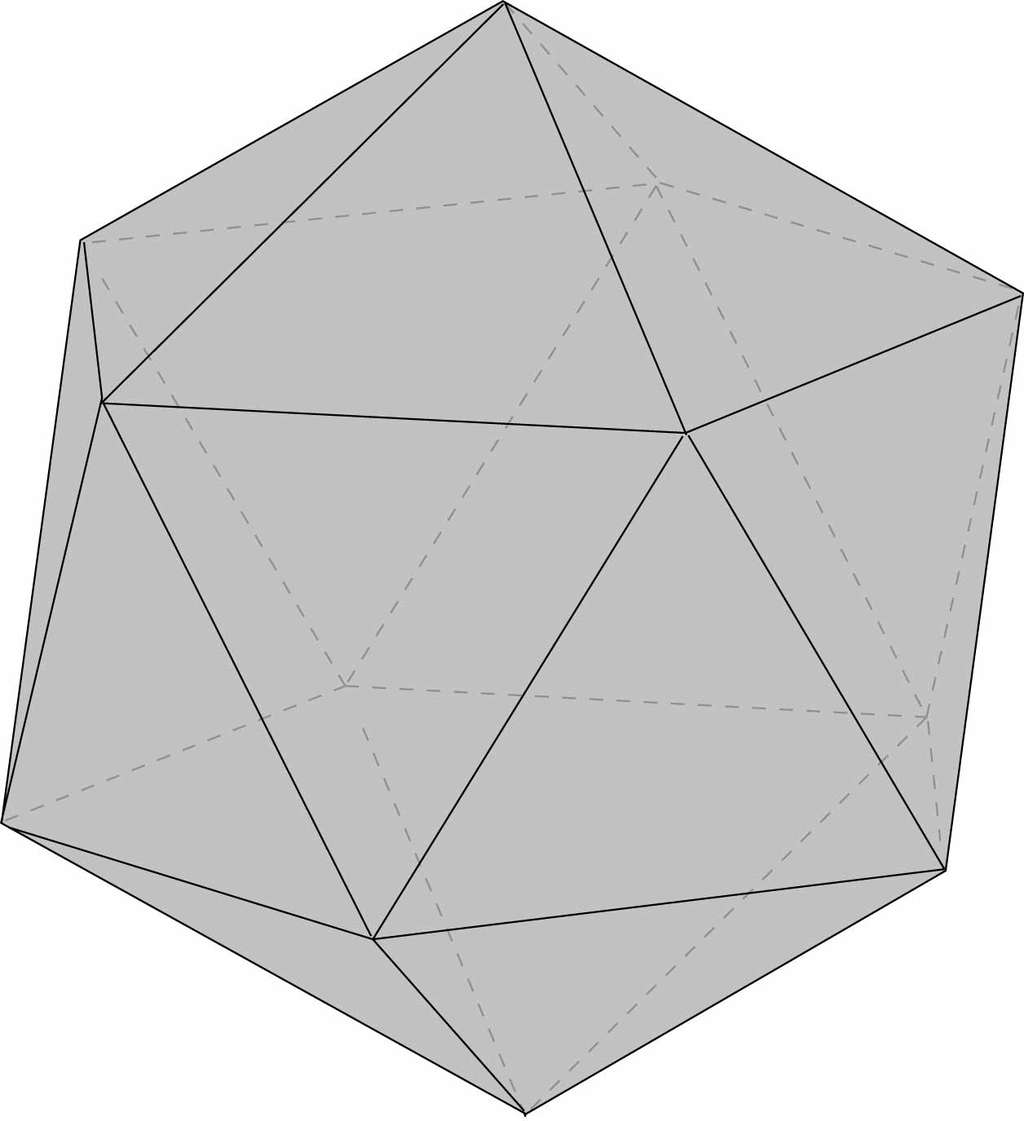
Le plus proche d'une sphère est l'icosaèdre. Malheureusement, même gonflé, ses pointes rendraient ses rebonds aléatoires. L'idée est de couper les pointes gênantes. On obtient l'icosaèdre tronqué. Il est formé de 12 pentagones et 20 hexagones.
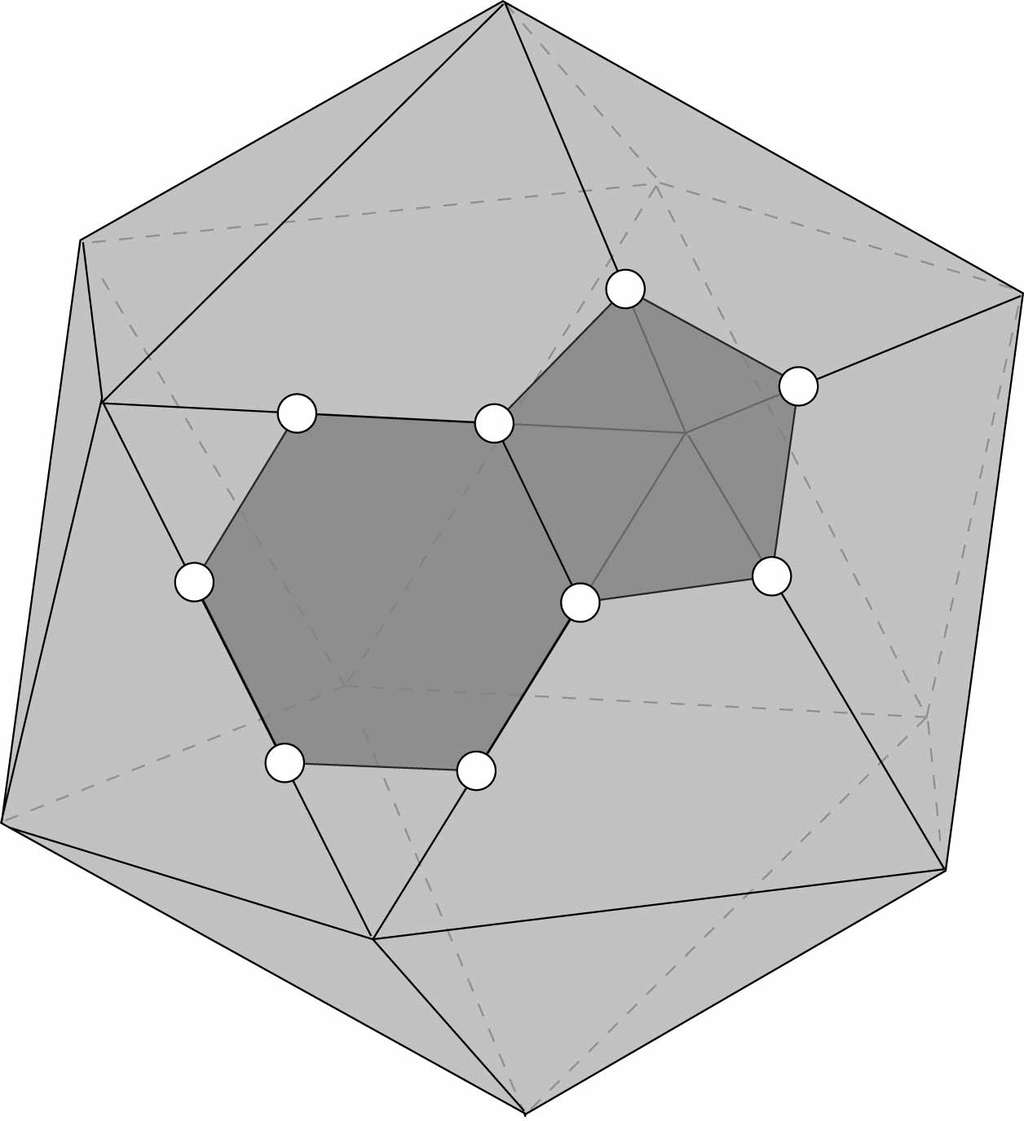
Nous obtenons ainsi le ballon de football. C'est ce profil anguleux qui lui permet d'accrocher l'air, quel que soit son degré d'usure et quelles que soient les conditions climatiques.

Un ballon de football n'est pas une sphère parfaite, ce qui accentue les effets. © Hervé LehningHervé Lehning, DR
L'effet Magnus au football
On obtient un effet en faisant tourner le ballon sur lui-même. Cet effet a été étudié scientifiquement par Heinrich Magnus (1802-1870), c'est pourquoi on l'appelle l’effet Magnus. Voici son mécanisme.
En tournant, le ballon entraîne l'air avec lui, d'autant mieux qu'il est irrégulier. Ce mouvementmouvement de rotation provoque une différence de pressionpression entre les deux côtés du ballon qui, de ce fait, est déporté du côté de la pression la plus faible. Selon la frappe du ballon, on peut produire plusieurs effets différents.
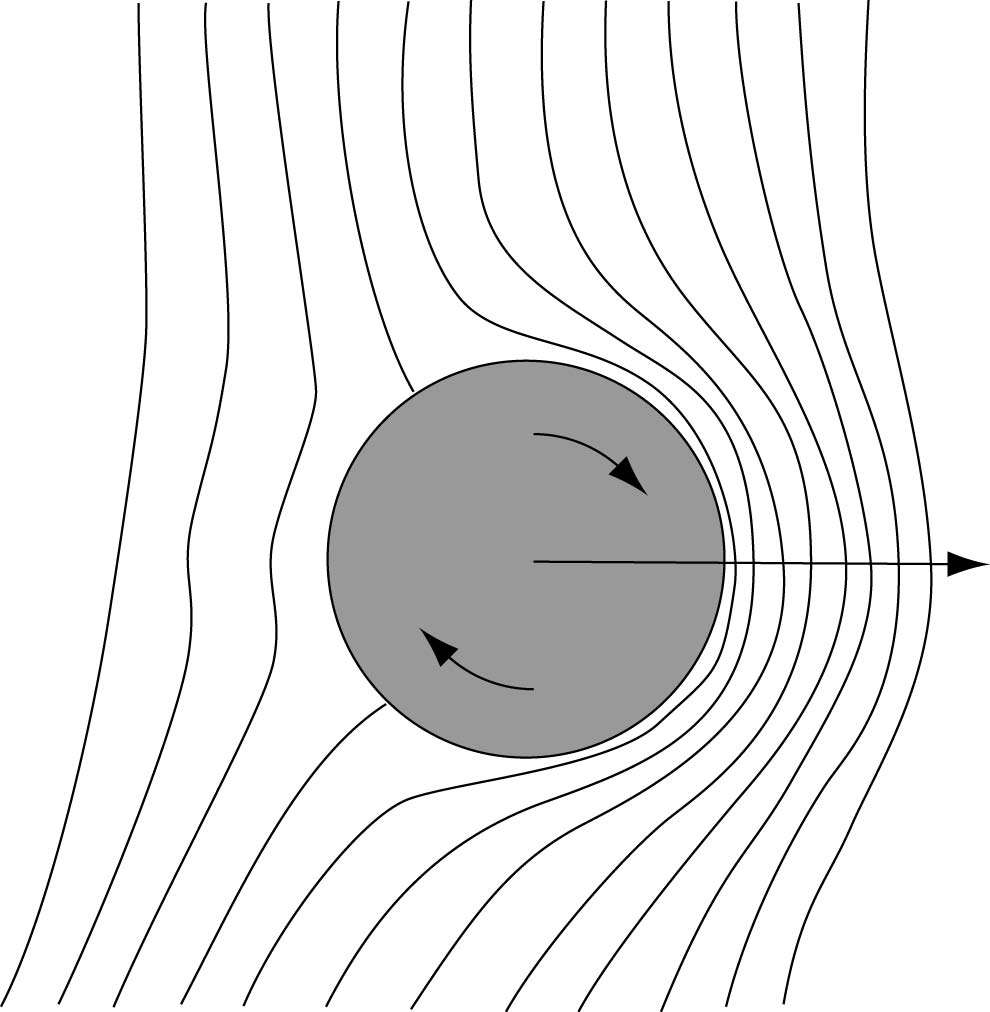
Pour couper un ballon, il suffit de le brosser de haut en bas, ce qui provoque sa rotation. La portée de sa trajectoire est diminuée et il rebondit moins haut. Le mouvement inverse a l'effet contraire, même s'il est plus difficile à réaliser. Enfin, on peut brosser le ballon sur le côté ce qui lui donne des effets étonnants.
L'air étant plus rare en altitude, les effets y sont diminués. Cela peut occasionner des surprises aux joueurs. Ainsi, lors du Mondial 1986, au Mexique, à 2.600 mètres d'altitude, Michel Platini a raté un coup franc décisif, sans doute parce qu'il n'avait pas tenu compte de cette différence.
Hervé Lehning
En savoir plus sur Hervé Lehning
Normalien et agrégé de mathématiques, Hervé Lehning a enseigné sa discipline une bonne quarantaine d'années. Fou de cryptographie, membre de l'Association des réservistes du chiffre et de la sécurité de l'information, il a en particulier percé les secrets de la boîte à chiffrer d'Henri II.
- Son blog MATH'MONDE sur Futura
- Le dernier livre d'Hervé Lehning :
À découvrir également : L'univers des codes secrets de l'Antiquité à Internet paru en 2012 chez Ixelles.


























