au sommaire
Il y a presque cinquante ans, avant que l'on ne découvre la théorie de la chromodynamique quantique, le grand théoricien britannique Tony Skyrme cherchait à mieux comprendre la nature des nucléons et des forces nucléaires fortes. On savait déjà que les protons et les neutrons étaient des fermions de spinspin demi-entier et qu'ils échangeaient des sortes de photonsphotons, le fameux bosonboson de Yukawa de spin entier, le pion.
À la même époque, Heisenberg cherchait lui aussi à mieux comprendre les forces nucléaires mais il allait plus loin. Il considérait une équationéquation de champ fondamental non linéaire basée sur un champ de fermions qui devait contenir toutes les particules de matièrematière et de force connues à l'époque. Dans cette théorie unifiée, photons et gravitons étaient par exemple vus comme des paquetspaquets de fermions. Ceux-ci ayant un moment cinétiquemoment cinétique intrinsèque, un spin, de valeurs respectives 1 et 2, ils pouvaient effectivement être des états liés d'un nombre pair de fermions de spin ½.
Un modèle pour les nucléons
Skyrme suivait une approche plus modeste (il ne s'occupait que des baryonsbaryons et des forces nucléaires) mais très similaire. Il considérait lui-aussi une équation non linéaire mais dont le champ fondamental était celui d'un boson de spin nul, le pion de Yukawa.
À première vue, l'idée semble absurde. Comment obtenir des particules de spin ½ à partir d'états composites de particules de spin nul ?
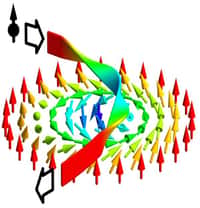
C'est là qu'intervient le caractère non linéaire de l'équation. De même que dans un fluide, lui aussi décrit par une équation non linéaire (celle de Navier Stokes), il peut se former des tourbillonstourbillons stables avec un moment cinétique, on pouvait considérer protons et neutrons comme des sortes de tourbillons dans un fluide de pions. Ces configurations, qui rappellent celles des solitonssolitons, sont aujourd'hui appelées des skyrmionsskyrmions.
La découverte des quarksquarks et de la théorie de la chromodynamique quantique (QCD) a éclipsé le modèle de Skyrme des baryons (ironiquement, il apparaîtra plus tard comme une approximation des équations de la QCD). Mais quelques décennies plus tard, on s'est aperçu de son importance dans le domaine de la physiquephysique de la matière condensée.
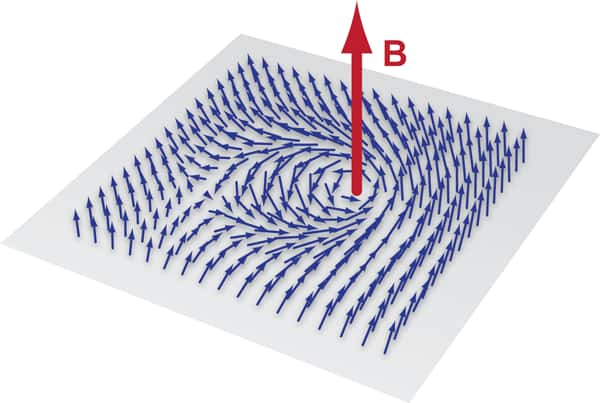
Un exemple de skyrmion émergeant dans un réseau d'atomes magnétiques en deux dimensions plongés dans un champ magnétique B (en rouge). Les atomes sont comme des petits aimants dont l'orientation magnétique est donnée par les flèches en bleu. On voit une sorte de tourbillon local formé par un soliton topologique. Le terme topologique s'explique par le fait qu'il n'est pas possible de transformer par déformation continue la distribution de flèches considérée en une autre sans tourbillons. C'est la même chose avec une sphère qui ne peut pas donner par déformation continue un tore puisque ce dernier possède une discontinuité, un trou. De même un tore n'est pas topologiquement équivalent à un bretzel puisque lui possède au moins deux trous. © Alan Stonebraker
En soi, ce n'est pas vraiment une surprise, d'ailleurs, au moment même où il a été proposé, nombreux étaient les physiciensphysiciens (tels Yoichiro Nambu)) qui essayaient de comprendre les caractéristiques des hadronshadrons et autres particules élémentairesparticules élémentaires en terme d'états collectifs non linéaires de particules plus fondamentales, à la façon de ce que l'on faisait déjà en physique du solidesolide. Le boson de Higgs est d'ailleurs un sous-produit des travaux dans le domaine de la supraconductivitésupraconductivité.
Un cristal de Skyrme
C'est dans le cadre de la théorie des milieux magnétiques que la théorie des skyrmions trouve aujourd'hui des illustrations intéressantes. Une publication dans Nature (donnée en lien ci-dessous) le montre bien. Des chercheurs des universités de Kiel et Hambourg s'étaient d'abord lancés dans l'investigation d'un certain type d'ordre magnétique à deux dimensions, sans rapport avec des skyrmions, dans une couche monoatomique de chromechrome déposée sur de l'iridiumiridium. La recherche, menée à l'aide d'un microscope à effet tunnelmicroscope à effet tunnel polarisé de spin, s'étant révélée infructueuse, les physiciens ont remplacé le chrome par du ferfer.
À leur surprise, un ordre magnétique inattendu est apparu. Modélisé à l'aide de calculs quantiques sur un supercalculateursupercalculateur, ils ont découvert qu'ils étaient en présence d'un cristal de Skyrme jamais observé jusqu'à présent.
En effet, si un réseau de skyrmions magnétiques avait déjà été observé il y a quelques années, il faisait intervenir des skyrmions formés d'un assez grand nombre d'atomesatomes et il n'apparaissait que sous l'influence d'un champ magnétiquechamp magnétique. Dans le cas présent, l'élément du cristal de Skyrme en deux dimensions n'est formé que de quinze atomes et, surtout, l'ordre magnétique apparaît spontanément sans l'intervention d'un champ magnétique extérieur.
Cette découverte pourrait avoir des applicationsapplications intéressantes dans le domaine de la spintronique.