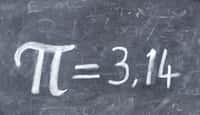Le virus de la Covid-19 a beau être extrêmement agressif, il est vraiment très, très petit. Christian Yates, un mathématicien de l’université de Bath (Royaume-Uni), s’est ainsi amusé à calculer l’espace que prendraient tous les virus SARS-CoV-2 actuellement en circulation si on les compactait au maximum.
au sommaire
Et s'il suffisait de mettre tous les coronaviruscoronavirus du monde dans une canette de Coca-Cola avant de la jeter à la poubelle ? Ce serait tout de même bien pratique pour s'en débarrasser ! Hélas, c'est rigoureusement impossible sur le plan pratique. Mais, en théorie, il serait effectivement possible d'y parvenir.
Pour arriver à cette conclusion, Christian Yates s'est livré à quelques approximations. Il a d'abord considéré uniquement les virus affectant les humains (exit donc les visons, chats et autres bébêtes infectées par le SARS-CoV-2SARS-CoV-2). Il a ensuite cherché à connaître le nombre de virus en circulation. Selon le site de statistiques Our World in Data, environ un demi-million de personnes obtiennent chaque jour un résultat positif au test de la Covid-19test de la Covid-19. Mais de nombreuses personnes ne sont pas dépistées. Le chiffre réel serait donc plus proche de 3 millions, estime l'Institute for Health Metrics and Evaluations.
Une démonstration graphique du calcul du volume des coronavirus dans le monde. © Vicki Martin, YouTube
Combien de virus dans un être humain ?
Deuxième étape : évaluer la quantité de virus maximale portée par un malade à un instant T. Christian Yates s'est inspiré d'une étude prépubliée sur le site MedRxiv qui a calculé le nombre de particules virales par gramme de différents tissus chez des singes infectés et a proportionnellement augmenté leur taille pour qu'ils soient représentatifs de l'humain. D'après les estimations de l'étude, les pics de charge viralecharge virale vont de 1 à 100 milliards de particules virales par individu. Pour simplifier, Christian Yates a pris la moyenne géométrique de cet intervalle, soit 10 milliards de particules virales par personne.
Mais ce n'est pas tout. On sait en effet que la charge virale augmente progressivement à partir de l'infection pour culminer le 6e jour et diminuer ensuite. Cela signifie qu'elle suit une courbe en cloche. « Lorsque l'on additionne toutes les contributions à la charge virale de chacune des 3 millions de personnes infectées les jours précédents (en supposant que ce taux de 3 millions soit à peu près constant), nous constatons qu'il y a environ 200 quadrillions de particules virales dans le monde à la fois », détaille Christian Yates dans son article paru sur le site The Conversation. Soit 200 millions de milliards ou 2 x 1017 virionsvirions.
“C'est à peu près le même nombre que celui des grains de sable sur la Planète”
« Cela semble énorme et c'est le cas. C'est à peu près le même nombre que celui des grains de sablesable sur la Planète », atteste le mathématicienmathématicien. Mais il n'y a largement pas de quoi couvrir les plages du monde, car le virus du SARS-CoV-2 est bien plus petit qu'un grain de sable : il mesure entre 80 et 120 nanomètres de diamètre, soit 1.000 fois plus mince qu'un cheveu humain. C'est là qu'intervient une autre (grosse) approximation qui consiste à considérer le virus comme parfaitement sphérique. Il suffit donc d'appliquer la simple formule de calcul du volume d'une sphère (V = 4π /3x r3), en prenant un diamètre moyen de 100 nanomètres (nm). On obtient alors 520.000 nm3 pour une particule virale. Reste à multiplier ce chiffre avec le nombre de particules, et on tombe sur un volume d'environ 120 millilitres (ml).

160 ml ou 52 fois la distance Terre-Lune
Attention, ce n'est pas fini ! Car, comme lorsque l'on empile des oranges dans une boîte en carton, il est impossible de remplir complètement un espace avec des sphères. Il faut donc calculer la proportion maximale du volume total occupé par les sphères. Ce problème d'empilement très célèbre, appelé conjecture de Kepler, n'a pourtant été démontré qu'en 1998 par Thomas Hales. Et encore, sa démonstration est tellement complexe que personne n'ose se porter garant de sa justesse, atteste Robin Jamet, du département de mathématiques au Palais de la Découverte. D'après ce théorème, on obtient une densité maximale d'environ 0,74 ; ce qui signifie que l'on a 26 % d'espace vide dans le contenant. Cela revient à augmenter le volume des virus à 160 ml. « Même en prenant en compte la taille des protéinesprotéines de pointe, tous les SARS-CoV-2 du monde ne rempliraient pas une canette de Coca-Cola », conclut Christian Yates. Et si on les alignait bout à bout, on arriverait à 52 fois la distance Terre-Lune.
Si les virus sont très petits, ils pèsent tout de même assez lourd. D'après l'étude de MedRxiv, la massemasse totale de tous ces virus se situe entre 100 g et 1 kgkg. Donc bien plus qu'une canette de Coca-Cola.