Présentation & historique des réseaux neuronaux

Historique

Le champ des réseaux neuronaux va démarrer par la présentation en 1943 par W. MCCulloch et W. Pitts du neurone formelneurone formel qui est une abstraction du neurone physiologique. Le retentissement va être énorme. Par cette présentation, ils veulent démontrer que le cerveaucerveau est équivalent à une machine de Turing, la pensée devient alors purement des mécanismes matériels et logiques. Il déclara en 1955 "Plus nous apprenons de choses au sujet des organismes, plus nous sommes amenés à conclure qu'ils ne sont pas simplement analogues aux machines, mais qu'ils sont machine." Mysterium Iniquitatis of Sinful Man Aspiring into the Place of God, repris in Embodiments of mind. La démonstration de McCulloch et Pitts sera un des facteurs importants de la création de la cybernétique.

En 1949, D. Hebb présente dans son ouvrage "The Organization of Behavior" une règle d'apprentissage. De nombreux modèles de réseaux aujourd'hui s'inpirent encore de la règle de Hebb.

En 1958, F. Rosenblatt développe le modèle du Perceptron. C'est un réseau de neurones inspiré du système visuel. Il posséde deux couches de neurones : une couche de perception et une couche lié à la prise de décision. C'est le premier système artificiel capable d'apprendre par expérience

Dans la même période, Le modèle de L'Adaline (ADAptive LINar Element) a été présenté par B. Widrow, chercheur américain à Stanford. Ce modèe sera par la suite le modèle de base des réseaux multi-couches.

En 1969, M. Minsky et S. Papert publient une critique des propriétés du Perceptron. Cela va avoir une grande incidenceincidence sur la recherche dans ce domaine. Elle va fortement diminuer jusqu'en 1972, où TT. Kohonen présente ses travaux sur les mémoires associatives. et propose des applications à la reconnaissance de formes.

C'est en 1982 que J. Hopfield présente son étude d'un réseau complétement rebouclé, dont il analyse la dynamique.

Aujourd'hui, les réseaux neuronaux sont utilisés dans de nombreux domaines (entre autres, vie artificielle et intelligence artificielleintelligence artificielle) à cause de leur propriété en particulier, leur capacité d'apprentissage, et qu'ils soient des systèmes dynamiques.

Les différentes formes de mémoires

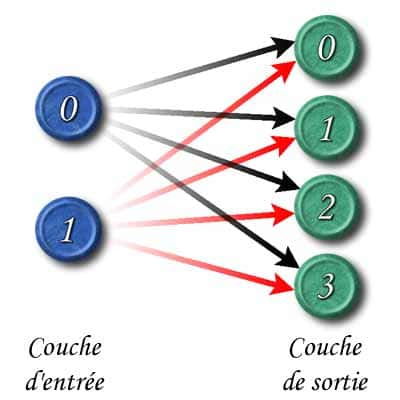
Les mémoires hétéro-associatives sont composées de deux couches, une couche d'entrées et une couche de sortie. Les neurones d'entrées sont reliés à la couche de sortie par des synapsessynapses. Chaque synapse possède un poids (entre 0 et 1 ou entre -1 et 1). Ce poids permet de faire corréler ou non l'activation d'un neurone de la couche d'entrée avec un neurone de la couche de sortie.

Les deux couches d'une mémoire hétéro-associative linéaire

Les sorties sont proportionnelles à l'activation. Les mémoires de ce type suivront donc cette formule.

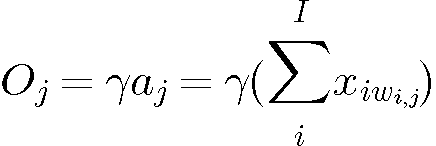
aj : activation du jème neurone de sortie
oj : intensité du jème neurone de sortie.
xi : intensité du ième neurone d'entrée.
wi,j : intensité du poids entre le ième neurone de la couche d'entrées et le jème neurone de la couche de sortie.
g : est un coefficient linéaire

Nous aurons aussi les matrices suivantes :

W = wi,j : la matrice des poids
X = xi,k : la matrice décrivant les K stimuli. la kème colonne représente le kéme stimulus ou exemple. Nous admettrons que les vecteurs xk sont normalisés.
A = aj,k : Elle correspond à la matrice des activations des neurones de sorties (donc la valeur en entrée de ces neurones). Nous avons donc A = WT.X O = oj,k : matrice de l'intensité des neurones j pour les stimuli k. nous avons donc .
T = tj,k ; matrice des réponses théoriques des neurones de sorties. C'est la comparaison de la matrice O et la matrice T qui permettra l'apprentissage supervisé.

Le problème est donc de trouver une matrice W qui permettrait idéalement d'avoir :

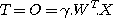
Voici quelques exemples de régles qui permettent d'approcher cette solution :

• la régle d'Hebb
• La régle du perceptron
• L'Adaline ou la régle de Widrow-Hoff

En complétement de ces mémoires hétéro-associatives, il existe les mémoires auto-associatives.

Les mémoires auto-associatives linéaires

Une mémoire est auto-associative si chaque stimulus est associé à lui-même. Ce type de mémoire permet de retrouver une information seulement avec des entrées partielles (données incomplétes). A l'opposé de la mémoire classique d'un ordinateurordinateur, l'information n'est pas accessible par une adresse, mais par un ensemble de connections.

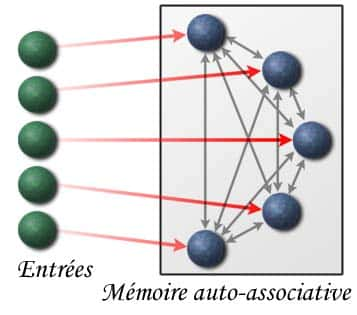
Exemple d'une architecture d'une mémoire auto-associative linéaire

Les neurones d'entrées sont reliés au neurone de la mémoire, mais en plus chaque neurone de la mémoire est relié à tout les neurones de la mémoire. Rappelons que le poids de chaque synapse doit être fort, si les deux neurones s'activent sur le même stimulus (régle de Hebb).

Les mémoires auto-associatives non linéaires : les réseaux de Hopfield

L'architecture d'un réseau de Hopfield ressemble beaucoup à une architecture de mémoire auto-associative linéaire. Cependant, il a deux caractéristiques importantes :

• la réponse est binairebinaire(1 ou -1)
• la réponse des neurones est asynchroneasynchrone

L'amnésieamnésie : le nombre d'exemple qu'un modèle de Hopfield est capable de mémoriser est environ 0.14 fois le nombre de neurones. Au délà, le réseau devient "amnésique" et oublie les précédents apprentissages.