Pourquoi voit-on deux rails parallèles se couper à l’infini ?

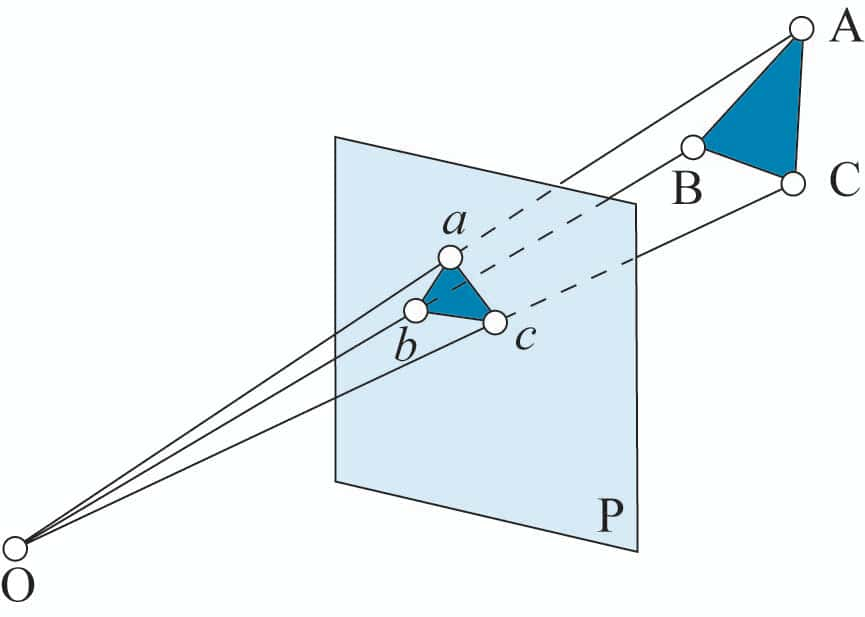
Comme la photographie, notre vision correspond à une projection centrale, une notion mathématique relativement simple. Plus précisément, si nous photographions un objet, l'image obtenue est la section par le plan de la pellicule (ou du capteurcapteur numériquenumérique) d'un cônecône dont le sommet est le diaphragmediaphragme de l'appareil et la base est l'objet photographié. La figure suivante montre la projection abc du triangle ABC dans la projection centrale de centre O sur le plan P.

Projections de droites parallèles

La projection centrale conserve l'alignement des points et l'intersection des droites mais pas les rapports de distance, et en particulier pas les milieux donc pas le parallélisme. Plus précisément deux droites parallèles de l'espace ne se transforment pas forcément en deux droites parallèles du plan P de projection. Les projections de deux droites parallèles peuvent donc se couper. La figure suivante montre un cas où les droites parallèles ABC et A'B'C' se transforment en deux droites abc et a'bc' sécantes en b.

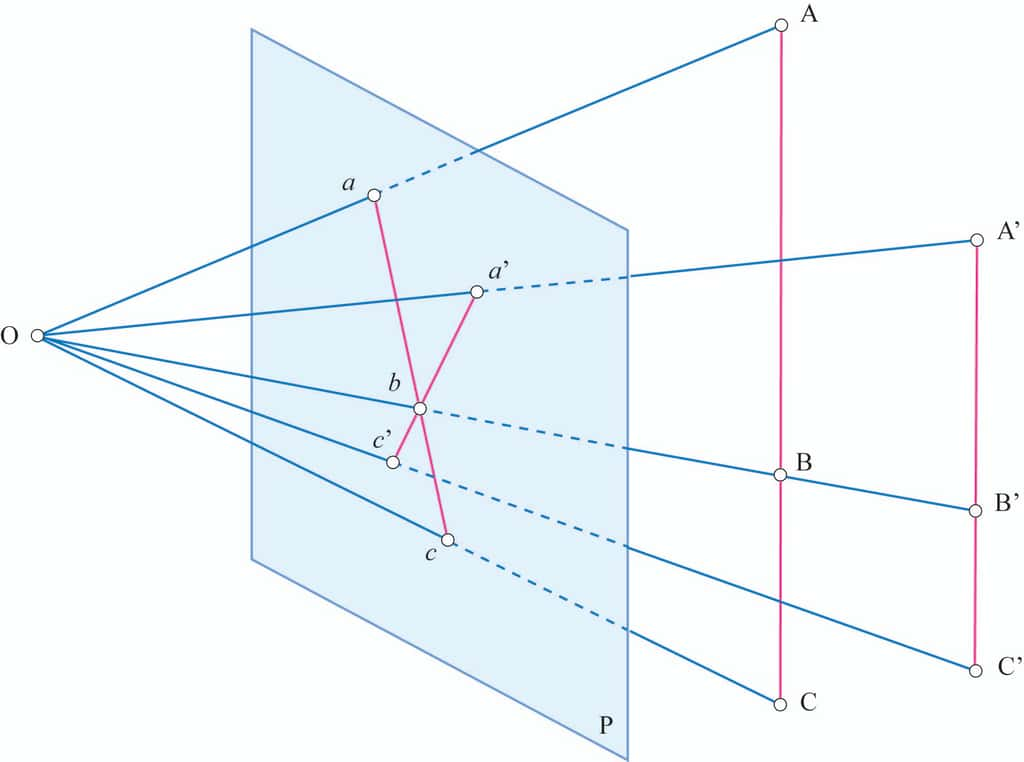
Un tel point est vu à l'infini puisque les deux droites sont parallèles. C'est ce que l'on constate en regardant des rails rectilignes sur un terrain plat comme sur la photographiephotographie.