Des températures négatives plus chaudes que l'infini avec des atomes ultrafroids

Depuis les travaux de Maxwell et Clausius sur la théorie cinétique des gaz, on sait que la chaleur et la température sont reliées à l'énergie cinétique d'agitation des particules dans un gaz, des molécules ou des solides. Lorsque cette agitation cesse dans un système physiquephysique, il ne contient plus de chaleur et sa température thermodynamiquetempérature thermodynamique absolue, telle que l'a définie William Thomson KelvinKelvin, devient nulle.

En théorie donc, il n'est pas possible d'obtenir des températures plus froides que le mythique zéro absoluzéro absolu qui vaut, par convention, -273,15 °C. Cette limite est même en fait inatteignable, ne serait-ce que parce que les inégalités de Heisenberg s'opposent à un gelgel complet de tous les mouvementsmouvements d'un système. Dans le cas d'oscillateurs harmoniques, par exemple ceux décrivant l'oscillation des atomesatomes aux nœudsnœuds d'un réseau cristallinréseau cristallin ou les fluctuations d'un champ quantique, cela se traduit par l'apparition d'une énergie minimale, la fameuse énergie du point zéro.

Le prix Nobel de physique Edward Purcell a été l'un des premiers à réaliser des expériences sur des systèmes à températures négatives. Il est surtout connu pour ses travaux sur la résonance magnétique nucléaire dans les liquides et les solides. © The Nobel Foundation

Une définition de la température liée à l'entropie

Il existe cependant une autre façon d'obtenir une notion de température sans la relier directement aux mouvements de particules. En effet, la formulation mathématique des principes de la thermodynamique montre que l'inverse de la température T d'un système physique est défini par la pente de la courbe de son entropieentropie S en fonction de son énergie interneénergie interne U.

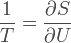
Dans la majorité des cas, en fait toujours lorsque l'on a affaire à un système décrit par la physique classique, la pente de cette courbe est positive. Mais dans certains systèmes quantiques, comme ceux définis à partir de l'énergie d'un système de spinsspins nucléaires plongés dans un champ magnétiquechamp magnétique, cette pente peut être négative et on obtient alors des températures négatives, comme le montre la courbe ci-dessous.

De tels systèmes ont été expérimentalement et théoriquement étudiés au début des années 1950, notamment par les prix Nobel de physique Edward Purcell et Norman Ramsey. Ce dernier a d'ailleurs publié un article dédié aux propriétés générales d'un système physique possédant une température thermodynamique négative.

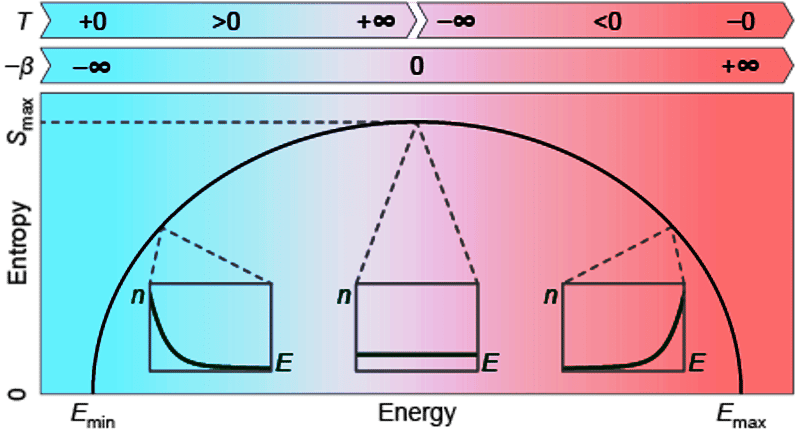
Sur ce schéma, on voit la courbe de variation de l'entropie (E) pour un système avec une énergie maximale (S_max). Cette courbe partage les états du système en deux régions. Le paramètre β correspond à 1/T, T étant la température. On voit donc qu'à gauche on est dans la partie des températures positives et à droite dans celle des températures négatives, les plus chaudes. Au centre, le système est à une température positive infinie. © Quantum Munich

La thermodynamique à températures négatives

Bien que respectant les lois de la thermodynamique, du moins lorsqu'on les formule convenablement, les systèmes avec des températures thermodynamiques négatives sont quelque peu paradoxaux. Si l'on met en contact un réservoir de chaleur à une température négative avec un autre, par exemple une bouteille d'héliumhélium liquideliquide, la chaleur va s'écouler du premier réservoir vers le second, donc des températures négatives vers les positives. Ce qui peut sembler contre-intuitif.

De fait, des systèmes à températures négatives sont toujours plus chauds que des systèmes à températures positives, de sorte que ces températures négatives sont plus élevées qu'une température positive infinie ! Pour mieux comprendre, il faut réaliser que porter un système à une température au-dessous du zéro absolu représente en réalité l'inverse d'un refroidissement sous le zéro. On respecte aussi la formulation de Clausius du second principe qui veut que la chaleur ne passe spontanément que d'un corps chaud à un corps froid.

Une autre conséquence paradoxale des systèmes à températures négatives, comme le soulignait Ramsey dans son article de 1956, est qu'il est possible de faire fonctionner un moteur thermiquemoteur thermique selon le cycle de Carnotcycle de Carnot avec un rendement supérieur à 1...

Températures négatives et inversion des populations

Il n'y a cependant aucune violation de la conservation de l'énergie. S'il est possible d'obtenir plus d'énergie sous forme de travail qu'il n'en a été prise sous forme de chaleur au réservoir thermique le plus chaud (donc celui à températures négatives), c'est parce que de la chaleur est aussi prise au réservoir le plus froid, c'est-à-dire celui à température positive.

La caractéristique imposée à un système physique pour exister à des températures négatives est de posséder une borne supérieure pour son énergie. On peut considérer par exemple les niveaux d'énergie d'une population finie d'atomes. D'ordinaire, les niveaux d'énergie sont d'autant plus peuplés qu'ils sont bas. Ajouter de la chaleur, donc de l'énergie interne, va augmenter le nombre d'électronsélectrons sur des niveaux d'énergie supérieurs mais on reste confronté à une sorte de pyramide des populations. Le système se trouve dans ce cas toujours sur la partie positive de la courbe ci-dessus où ajouter de l'énergie fait croître son entropie.

Mais si l'on réalise une inversion des populations, comme c'est le cas lorsque l'on réalise un masermaser ou un laser, c'est-à-dire en renversant la pyramide des populations des particules sur les niveaux d'énergie, alors l'entropie décroît lorsque l'on augmente l'énergie du système. On est alors sur la partie descendante de la courbe précédente et donc en présence d'un système à températures négatives.

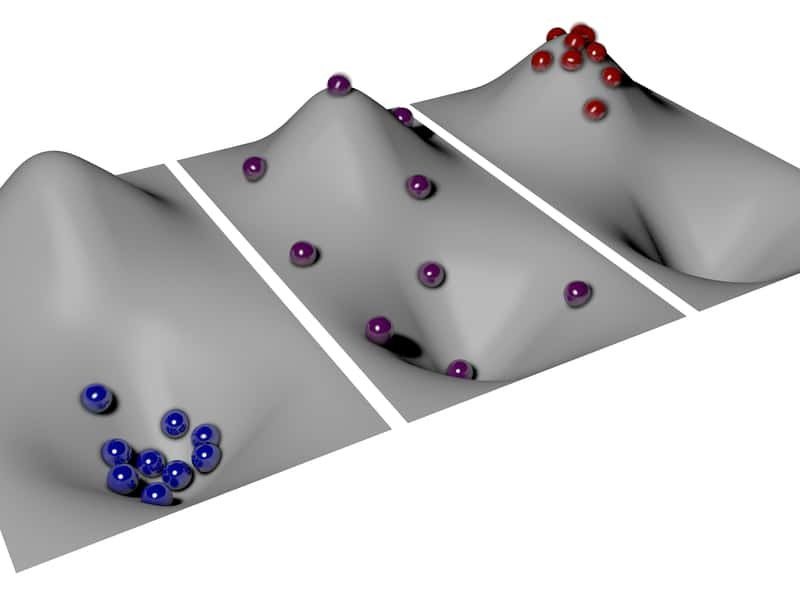
Une autre façon de voir l'obtention de températures négatives. La surface en gris correspond à des états d'énergies bornés pour des particules formant un système physique. Pour des températures positives, la majorité des particules se retrouvent dans des états d'énergies minimaux au fond d'une cuvette de potentiel (particules bleues, à gauche). Lorsque la température positive s'approche de l'infini, tous les états d'énergie possibles sont uniformément peuplés (au milieu). Dans le régime des températures négatives, les particules sont localisées vers les états d'énergies maximaux formant un pic (particules rouges, à droite). C'est l'inversion des populations. © Ludwig-Maximilians University

Des températures négatives avec de l'énergie cinétique

En physique classique, l'énergie cinétique des particules d'un gaz peut croître sans limite. L'énergie d'un gaz dans une bouteille n'est donc pas bornée et il n'est donc pas possible de le porter à des températures négatives. Pourtant, un groupe de chercheurs allemands de l'université Ludwig-Maximilians, à Munich, et du Max PlanckMax Planck Institute of Quantum Optics de Garching vient de contourner cet obstacle en obtenant des températures négatives à l'aide d'un gaz d'atomes ultrafroids de potassiumpotassium dans un réseau optique, comme il est expliqué dans un article de Science.

La clé de cet exploit est, bien sûr, que l'on n'est plus ici en physique classique mais bien dans un domaine gouverné par les lois de la physique quantiquephysique quantique.

Rappelons qu'un réseau optique est une sorte de piège pour atomes réalisé avec des faisceaux laserlaser sous un vide poussé. Les atomes s'y retrouvent presque immobilisés à des températures inférieures à un microkelvin au-dessus du zéro absolu. Ils occupent l'équivalent des cuvettes de potentiel des atomes dans un cristal, ici formées par des ondes stationnaires. Il devient possible de cette façon de simuler bien des matériaux en ajustant les paramètres du réseau optique de manière à obtenir différentes forces répulsives ou attractives entre les atomes.

Dans le cas présent, les physiciensphysiciens ont donc obtenu l'équivalent d'un gaz à une température négative de quelques milliardièmes de kelvin sous le zéro absolu à partir, non pas des niveaux d'énergie discrets d'un système de spin nucléaire, mais des énergies cinétiques et potentielles combinées d'atomes de potassium 39, parce que l'énergie totale de ce gaz quantique se retrouve bornée, avec une valeur maximale possible intrinsèque. C'est une première.