Même si regarder un ciel étoilé en donne une idée, l’infini n’est pas une notion physique mais un idéal mathématique… utile dans les calculs. Les mathématiciens distinguent deux notions, dont seule la première peut avoir un sens dans la réalité.
au sommaire
Quelles sont les notions d'infini ?
L’infini potentiel
La première notion d’infini est l'infini potentiel. Quand on affirme que l'ensemble des nombres entiers (1, 2, 3, etc.)) est infini, on utilise cette notion : tout nombre peut être dépassé. Si je vous demande de me donner un grand nombre, je pourrai toujours en trouver un plus grand : en lui ajoutant 1 par exemple. Dans l'Antiquité, les mathématiciensmathématiciens n'admettaient que cette notion d'infini. Les physiciensphysiciens peuvent l'admettre également facilement.
L’infini actuel
Le véritable infini, celui que refusent les physiciens, se nomme l'infini actuel. Le mot « actuel » doit ici être pris dans le sens de « effectif », comme le « actual » anglais. L'envisager dans certains calculs est intéressant en mathématiques où la considération de quantités infiniment petites permet de résoudre certains problèmes. Cette notion permet également de considérer des sommes infinies comme : S = 1/2 + 1/4 + 1/8 + 1/16 + etc. Leur donner un sens est une affaire plus délicate. Dans ce cas, un petit dessin aide à le faire :
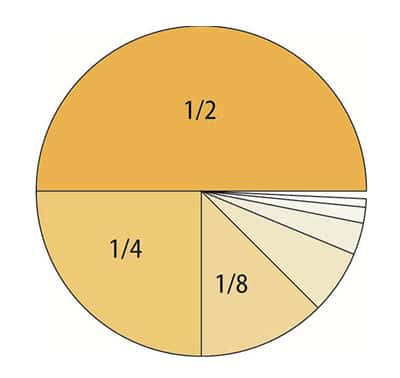
Ce partage géométrique montre que : S = 1. Il reste que ce partage ne peut se réaliser que dans l'idéal car, très vite, les morceaux ne sont que des miettes.
Conclusion
La réponse à la question posée sur l'existence de l'infini dépend donc du sens qu'on donne au mot « exister ». S'il s'agit d'existence dans la réalité matérielle, la réponse est non. S'il s'agit d'existence en tant que concept mathématique utile, la réponse est oui.
Hervé Lehning
En savoir plus sur Hervé Lehning
Normalien et agrégé de mathématiques, Hervé Lehning a enseigné sa discipline une bonne quarantaine d'années. Fou de cryptographie, membre de l'Association des réservistes du chiffre et de la sécurité de l'information, il a en particulier percé les secrets de la boîte à chiffrer d'Henri II.
- Son blog MATH'MONDE sur Futura
- Le dernier livre d'Hervé Lehning :
À découvrir également : L'univers des codes secrets de l'Antiquité à Internet paru en 2012 chez Ixelles.