Jeu mathématique : qu’est-ce que le postulat d’Euclide ?

Dans Les Éléments d'Euclide (III^e siècle avant notre ère), le postulat vient après les définitions des points, des droites, du parallélisme (deux droites sont parallèles si elles ne se coupent pas), des angles, etc.

La somme des angles d’un triangle

Le postulat est lié au fait que la somme des angles d'un triangle soit égale à 180°. La démonstration de cette propriété ouvre la voie aux géométries non euclidiennes, c'est-à-dire celles qui nient le postulat.

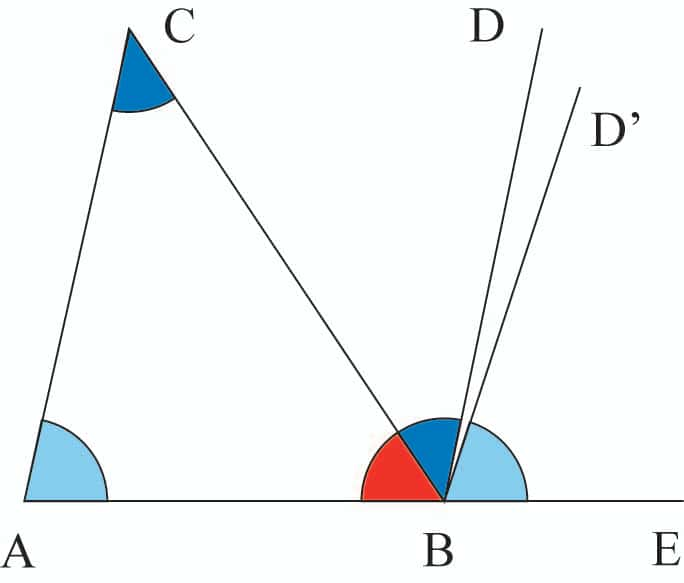
Considérons un triangle ABC et prolongeons le côté AB en BE. Puis, du point B, portons la droite BD de sorte que l'angle CBDCBD soit égal à l'angle ACB (les deux en bleu foncé). De même, portons la droite BD' de façon que l'angle EBD' soit égal à l'angle BAC (en bleu clair). Les droites BD et BD' sont parallèles à la droite AC. Si le postulat est vrai, elles sont identiques puisque, d'un point, on ne peut tracer qu'une parallèle à une droite donnée. Les trois angles du triangle ABC (le troisième en rouge) se reportent ainsi en B pour former un angle plat, c'est-à-dire 180°. Nous avons ainsi démontré que la somme des angles d'un triangle est égale à 180°... si le postulat d’Euclide est vrai. Quand nous dessinons la figure précédente sur une feuille de papier, les droites BD et BD' sont confondues.

En courbant le plan…

Coupons le papier le long de la demi-droite BD et déplaçons BD' sur BD, la feuille se courbe. Elle devient comme un sommet de montagne et la somme des angles du triangle, supérieure à 180°. Au contraire, en écartant BD' de BD, la feuille se courbe dans l'autre sens. Elle devient comme un col de montagne et la somme des angles du triangle, inférieure à 180°. La première est la géométrie sphérique ou de Riemann, la seconde, la géométrie hyperbolique ou de Lobatchevski (1792 - 1856).