Comment empiler des oranges pour qu’elles occupent le moins de place possible dans un emballage ? Cette question apparemment fantaisiste a intéressé Johannes Kepler et a préoccupé des physiciens pendant des siècles. La réponse a été trouvée en trois dimensions il y a plus de 20 ans. Une généralisation de ce problème en n dimensions a ensuite été considérée et la mathématicienne ukrainienne Maryna Viazovska a trouvé il y a quelques années les solutions à ce problème en dimension 8 et 24. Cela lui vaut aujourd'hui la médaille Fields de mathématiques.
au sommaire
En 2014, comme tous les quatre ans depuis 1950, le Congrès international des mathématiciensmathématiciens (ICM, International Congress of Mathematicians)) décernait à quatre lauréats la médaille Fields qui est souvent considérée comme le prix Nobel des mathématiques. Il créait la surprise en l'attribuant pour la première fois à une femme, la mathématicienne d’origine iranienne Maryam Mirzakhani, hélas décédée depuis.
À ce moment-là et depuis, les premières attributions de la Médaille à partir de 1936 à des mathématiciens qui doivent être âgés de moins de 40 ans, les plus de 50 lauréats passés avaient tous été des hommes. On apprend donc avec plaisir que l'une des nouvelles médailles Fields attribuées en 2022 lors du Congrès international de mathématiques qui s'est ouvert à Helsinki, en Finlande, revient à la mathématicienne d'origine ukrainienne Maryna Viazovska. Âgée de 37 ans, née à Kiev en Ukraine le 2 décembre 1984, elle rejoint donc le club des plus de 60 mathématiciens récompensés à ce jour par la mythique médaille.
Maryna Viazovska est lauréate du prestigieux prix, considéré comme le prix Nobel des mathématiques. Il récompense son travail sur les empilements de sphères dans les dimensions 8 et 24, alors qu’avant ses recherches, aucune démonstration ne permettait de dépasser les 3 dimensions. Une autre médaille Fields revient à Hugo Duminil-Copin, professeur à l’université de Genève. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © EPFL
L'événement a bien évidemment une résonance particulière avec les événements actuels en Ukraine, mais il faut savoir que l'attribution de la médaille Fields avait été signifiée à Maryna Viazovska en février 2022, avant l'invasion de l'Ukraine lancée par Vladimir Poutine. La mathématicienne ne peut cependant pas ne pas mentionner ce fait dans la vidéo réalisée à l'occasion de la remise de cette récompense et où elle donne aussi quelques explications concernant la découverte qu'elle a faite et qu'elle a rendue publique en 2016 avec un article déposé sur arXiv.
Une généralisation du problème de Kepler en dimensions supérieures
Techniquement, et dans le jargon familier aux mathématiciens, Maryna Viazovska a réalisé et démontré qu'une élégante combinaison de concepts mathématiques à l'intersection de plusieurs grands domaines de recherche, à savoir la théorie des groupes et algèbres de Lie, la théorie des formes modulaires que l'on retrouve étroitement liée à la théorie des fonctions analytiques dites elliptiques et aux transformations conformes du plan complexe, et enfin à ce que l'on appelle l'analyse harmonique avec les transformées de Fourier et la théorie des distributions (que l'on doit à un autre lauréat de la médaille Fields, le Français Laurent Schwartz) permettait de résoudre en dimension 8 et 24 un problème dont la solution en dimension 3 avait été conjecturée en 1611 par l'astronomeastronome et mathématicien Johannes KeplerJohannes Kepler. Il s'agissait de trouver l'empilement optimal de sphères avec un minimum de vide entre elles.
Le problème est moins trivial qu'il n'y paraît car, comme Futura l'avait expliqué dans un précédent article, on peut avoir besoin de le résoudre en partie pour comprendre la structure de la matière, notamment quand elle est cristallisée, à partir de la théorie atomique en considérant un modèle simple des atomes sous la forme de sphères compactes. Historiquement, il semble aussi que ce problème vient également de celui de savoir comment stocker le plus grand nombre de boulets de canon dans un volume donné. Les mathématiciens et les physiciensphysiciens ont donc cherché depuis des siècles à déterminer comment empiler des sphères de la façon la plus efficace possible et c'est dans les écrits de Kepler que l'on trouve, pour la première fois, la conjecture portant son nom et qui ne fut démontrée qu'en 1998 grâce au mathématicien Thomas Hales.
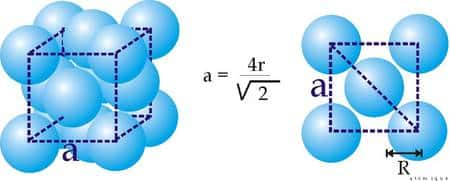
D'après Kepler, l'empilement le plus efficace était celui donnant une structure cubique à face centrée que l'on connaît justement bien aujourd'hui en théorie des réseaux cristallins. Un tel « pavage » d'un volume par des sphères permet d'occuper environ 74 % d'un volume donné.
De telles considérations sont utiles pour expliquer la densité d'un cristal par exemple, et prédire aussi dans quelle mesure on peut y introduire des atomes d'un type différent et occupant un volume sphérique plus petit que ceux ayant initialement servi pour constituer ce cristal. La conception d'alliages avec des propriétés données bénéficie des recherches sur ces questions.
Maryna Viazovska reçoit la médaille Fields 2022 pour la preuve que le réseau E8 fournit le garnissage le plus dense de sphères identiques en 8 dimensions, et d'autres contributions aux problèmes extrémaux et aux problèmes d'interpolation connexes dans l'analyse de Fourier. Elle donne des explications sur son travail à l'origine de la médaille Fields dans cette vidéo. Pour obtenir une traduction en français assez fidèle, cliquez sur le rectangle blanc en bas à droite. Les sous-titres en anglais devraient alors apparaître. Cliquez ensuite sur l'écrou à droite du rectangle, puis sur « Sous-titres » et enfin sur « Traduire automatiquement ». Choisissez « Français ». © International Mathematical Union
De Kyiv à l’école polytechnique fédérale de Lausanne
On peut trouver sur la page de l'International Mathematical Union plusieurs liens qui permettent d'en apprendre plus sur le parcours de la mathématicienne ukrainienne et sur les travaux qui lui ont valu la médaille Fields.
Il y a ainsi une interview qui avait commencé le 18 février 2022 et qui s'est poursuivie le 6 juin 2022, conduite par deux mathématiciens russes Andrei Okounkov et Andrei Konyaev. Le premier a également été lauréat de la médaille Fields, mais en 2006. Futura avait consacré un article à son travail à cette époque.
Dans cette interview, Maryna Viazovska explique qu'elle vient d'une famille de chimistes et qu'elle s'est très tôt passionnée pour les mathématiques. « Nous n'avons pas de mathématiciens dans la famille ; ma mère, mon père, ma grand-mère et mon grand-père sont tous chimistes. Il me semble que mon histoire est assez banale. Quand j'avais 12 ans, je suis entrée dans une école spécialisée en physiquephysique et en mathématiques et j'ai commencé à participer à des olympiades de mathématiques. Puis j'ai compris que je voulais être mathématicienne. »
Dans un autre extrait de son interview, elle expose d'autres éléments de son parcours : « Je me souviens d'avoir eu un livre dans lequel le théorèmethéorème fondamental de l'algèbre était prouvé par des méthodes topologiques. Parmi les problèmes d'olympiade, j'ai préféré ceux de combinatoire, surtout les plus anciens. Ils peuvent nécessiter une seule idée, mais une très belle. Dans les problèmes plus récents, on pouvait avoir à empiler plusieurs idées ensemble - comme si vous faisiez un sandwich. Je me souviens aussi - cela n'a peut-être rien à voir avec les maths - que nous avions un voisin qui est mort il y a longtemps. C'était un vieil homme qui avait combattu pendant la grande guerre et qui avait ensuite travaillé avec mon grand-père à la même université. Et il avait une énorme - vraiment énorme ! - collection de différents livres populaires sur la physique et les mathématiques à la maison. Et puis à un moment donné, je pense que ses petits-enfants ne se sont pas engagés dans des études scientifiques, il me les a donnés. Toute la collection, toute la pile. Et là, j'ai trouvé un livre d'astronomie qui m'a vraiment impressionné. » Elle citera plus tard parmi les livres de géométrie qu’elle a lus un de ceux du mathématicien ukrainien Aleksei Pogorelov. On peut trouver nombre d'ouvrages remarquablement pédagogiques des mathématiciens de l'ex-URSS traduit en anglais qui sont archivés.
Quant à sa découverte d'une généralisation de la solution du problème de Kepler en dimension 8 et 24, on peut la comprendre au moins dans les grandes lignes avec un bagage de L3 en mathématique et en s'aidant de l’exposé qu’en fait pour le public cultivé de ce niveau à nouveau Andrei Okounkov.
On y apprend que cela a à voir avec l'équivalent mathématique des réseaux cristallins et des groupes de symétrie associés à la géométrie de ces réseaux. Or, on sait qu'en physique on peut analyser les réseaux cristallins d'atomes avec la théorie des transformations de Fouriertransformations de Fourier à l'aide d'expériences de diffractiondiffraction. On n'est donc finalement pas très surpris que des solutions généralisées en dimensions supérieures à 3 du problème de Kepler fassent intervenir l'analyse harmonique en relation avec la théorie des groupes. On sait aussi que des symétries en rapport avec des réseaux cristallins peuvent être connectées à la théorie des fonctions de la variable complexe et plus précisément avec celles de ces fonctions que l'on appelle des fonctions elliptiques et en relation avec la théorie des surfaces de Riemann ainsi qu'avec des travaux mythiques du mathématicien français Henri Poincaré concernant ce que l'on appelle les fonctions automorphesautomorphes.
Remarquablement, en dimension 8, un des ingrédients clé de la démonstration de Maryna Viazovska est relié au fameux groupe de Lie exceptionnel de la théorie des supercordes : E8.