Jeu mathématique : les roues d'Aristote

Dans « Les Mécaniques », un texte attribué à Aristote redécouvert à la Renaissance, on trouve un paradoxe intéressant. Le voici. Deux cercles concentriques de rayons différents, dont l'un entraîne l'autre, parcourent, en roulant le même chemin rectiligne. L'un et l'autre achèvent un tour complet au même instant.

Les roues d'Aristote. © Hervé Lehning, tous droits réservés

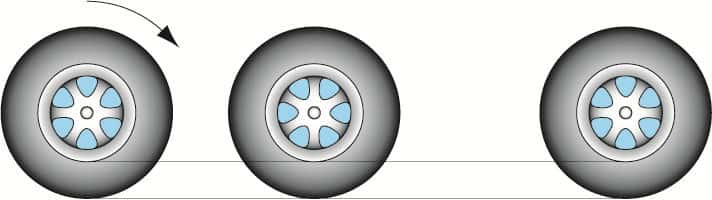
Le paradoxe consiste à en conclure l'égalité des circonférences, ce qui est manifestement faux.

Question :

Mais où est l'erreur ?

Réponse :

Du point de vue mécanique, la question est simple : si la grande roue roule sans glisser, la petite glisserait... si elle était en contact avec le sol. Galilée a répondu à ce paradoxe dans l'esprit du calcul infinitésimal naissant. Il approxime le cercle par un polygone régulier et, pour commencer, par un hexagone. Il fait tourner l'ensemble des deux hexagones afin de passer d'un côté du grand au suivant. La surprise vient de la suite des petits côtés, quand ils se succèdent à l'horizontale, car on y trouve des trous.

Déplacement des hexagones. © Hervé Lehning, tous droits réservés

Quand l'ensemble des deux hexagones tournent, les côtés du grand se succèdent l'un derrière l'autre, mais pas ceux du petit. Entre deux consécutifs, il y a un trou. Quand le nombre de côtés des polygones augmente, ils se rapprochent des deux cercles et les trous diminuent de taille. On obtient bien deux segments de même longueur mais le second, celui qui correspond au petit cercle, est rempli de trous.