au sommaire
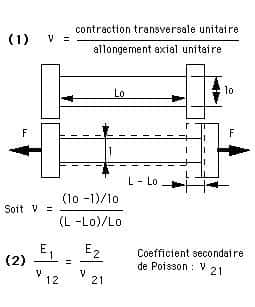
Coefficient de Poisson
Le coefficient principal de Poisson permet de caractériser la contraction de la matière perpendiculairement à la direction de l'effort appliqué.
Ce coefficient a été mis en évidence analytiquement par Denis PoissonPoisson, mathématicien Français (1781 - 1840), auteur de travaux sur la physique mathématique et la mécanique, qui en détermina la valeur à partir de la théorie moléculaire de la constitution de la matière. Il est défini par la formule n°1 ci-contre.
Désigné par la lettre grecque ν, le coefficient de Poisson fait partie des constantes élastiques (2 pour un matériau isotrope ou 4 pour un matériau isotrope transverse). Il est théoriquement égal à 0,25 pour un matériau parfaitement isotrope et est en pratique très proche de cette valeur.
Dans le cas d'un matériau isotrope, le coefficient de Poisson permet de relier directement le module de cisaillement G au module de Young E.
Le coefficient de Poisson est toujours inférieur ou égal à 1/2. S'il est égal à 1/2, le matériau est parfaitement incompressible.
Dans le cas d'un stratifié (isotrope transverse), on définit un coefficient secondaire de Poisson défini par la relation n°2 ci-contre reliant E1 et E2.
Compréhension approfondie du coefficient de Poisson
Le coefficient de Poisson, souvent noté ν, est un paramètre crucial en mécanique des matériaux car il fournit des indications sur le comportement déformatif des matériaux sous charge. Ce coefficient mesure le rapport entre la contraction latérale et l'extension longitudinale d'un matériau lorsqu'il est étiré. Une valeur élevée du coefficient de Poisson indique que le matériau subit une grande contraction latérale en réponse à une extension longitudinale, révélant ainsi son degré de compressibilité ou d'incompressibilité. Cette caractéristique est essentielle dans les applicationsapplications d'ingénierie où les matériaux sont soumis à divers types de charges.
Applications pratiques et impact sur les matériaux
La connaissance du coefficient de Poisson est cruciale dans de nombreux domaines tels que l'ingénierie civile, les matériaux composites, la métallurgie et la bio-ingénierie. Par exemple, dans la conception de structures telles que des ponts ou des bâtiments, une compréhension précise du coefficient de Poisson des matériaux utilisés peut influencer la sécurité et la stabilité de la structure. De même, dans le secteur biomédical, les prothèsesprothèses et les implantsimplants doivent souvent imiter les propriétés mécaniques du corps humain, y compris son coefficient de Poisson, pour garantir une intégration et une fonctionnalité efficaces.
Relation entre le coefficient de Poisson et d'autres propriétés mécaniques
Le coefficient de Poisson est intrinsèquement lié à d'autres propriétés mécaniques des matériaux telles que le module de Youngmodule de Young et le module de cisaillement. Ces relations sont utilisées pour décrire le comportement mécanique des matériaux sous différentes charges et contraintes. Par exemple, la formule qui relie le module de cisaillement (G) et le module de Young (E) à travers le coefficient de Poisson (ν) est :
- G = E / [2(1 + ν)]
Cette relation montre comment trois constantes élastiques fondamentales interagissent pour définir les propriétés de déformation d'un matériau.
Mesure et expérimentations
La détermination expérimentale du coefficient de Poisson se fait généralement à travers des tests de traction où la déformation longitudinale et la contraction transversale sont mesurées. Ces données permettent de calculer directement le coefficient de Poisson en utilisant la formule ν = - (contraction transversale / extension longitudinale). La précision de ces mesures dépend fortement des équipements utilisés et de la qualité de la préparation des échantillons.
























