au sommaire
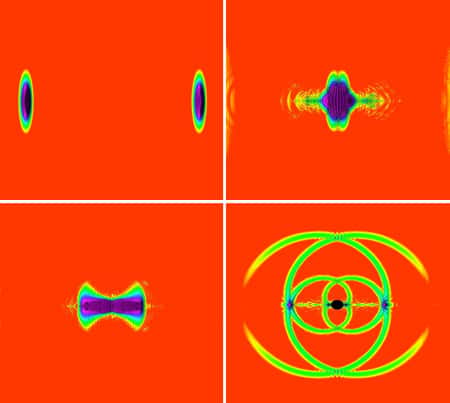
Quelques images des simulations numériques de Pretorius et Choptuik. On débute en haut à gauche par deux étoiles bosoniques dont l'apparence est contractée longitudinalement par des effets relativistes. En bas à droite, la zone noire montre l'apparition d'un trou noir. L'image montre l'intensité du champ scalaire des particules des étoiles bosoniques. Crédit : Frans Pretorius
Prenez n'importe quel objet de masse M et comprimez-le suffisamment. Il deviendra un trou noir. Il suffit pour cela qu'il occupe un volume inférieur à celui d'une sphère dont le rayon est égal à celui de Schwarzschild déterminé par cette masse. Celui-ci vaut Rs=2GM/C2 où G et C sont respectivement la constante de la gravitation de Newton et C la vitesse de la lumièrevitesse de la lumière.
On pourrait croire qu'un objet accéléré presque à la vitesse de la lumière doit lui aussi devenir un trou noir. Après tout, il possède alors une énorme énergieénergie associée à un corps d'une taille donnée. Il n'en est rien. Si cela devait se produire, un observateur en mouvementmouvement à cette vitesse devrait se sentir comprimé par le champ de gravitation associé à cette énergie cinétiqueénergie cinétique et au-delà d'un certain seuil devrait s'effondrer sur lui-même. Cela serait en violation avec le principe de relativité même qui stipule qu'aucune expérience de physiquephysique ne permet de dire si un objet est en mouvement absolu à une vitesse rectiligne et uniforme.
Il n'en reste pas moins que l'on s'attend bel et bien à la formation d'un trou noir lorsque DEUX objets se déplaçant à la vitesse de la lumière entrent en collision et se retrouvent dans un volume avec un rayon de Schwarzschildrayon de Schwarzschild donné par l'énergie totale des deux objets. Il s'agit en fait d'un cas particulier de ce que l'on appelle la conjectureconjecture du cerceau de Kip Thorne.

Kip Thorne à Caltech. Crédit : Wikipédia
Tout dépend de la masse de Planck...
Kip Thorne avait en effet constaté que des objets de formes différentes devenaient des trous noirs dans le cadre des calculs de la relativité généralerelativité générale lorsqu'ils se trouvaient comprimés en dessous de la sphère déterminée par la rotation d'un anneau ayant comme valeur du rayon Rs.
Aucune démonstration générale de cette conjecture n'a encore été donnée, mais aucun contre-exemple non plus. Mieux, même au sein d'extensions de la théorie de la relativité générale prenant en compte des espaces-tempsespaces-temps à plus de 4 dimensions, la conjecture de Thorne semble toujours vérifiée.
Steven Giddings a été un des premiers à proposer que la création de mini trous noir dans le cadre des théories à basses masses de PlanckPlanck soit possible au LHCLHC. On sait en effet que dans le cadre de la théorie d'EinsteinEinstein classique, avec une masse de Planck de l'ordre de 1016 TeV il faudrait, pour qu'un trou noir se forme, un collisionneur de 100.000 années-lumièreannées-lumière de diamètre pour charger suffisamment en énergie une petite région de l'espace-temps au moyen d'une collision de protonsprotons. Mais dans des théories comme celles des supercordes ou de Kaluza-Klein qui prolongent les équationséquations d'Einstein pour unifier, matièrematière, gravitation et forces du modèle standardmodèle standard, il devient alors possible que les 14 TeV disponibles à terme dans les collisions au LHC soient suffisants. La condition est que la masse de Planck soit comprise entre quelques TeV et ces 14 TeV.
Sauf que personne n'avait calculé en détail ce qui apparaît quand on résoud rigoureusement les équations non linéaires d'Einstein décrivant une collision entre deux particules.
Giddings et d'autres avaient quand même considéré des situations assez réalistes dans lesquelles on faisait intervenir des collisions de trous noirs à l'aide de ce qu'on appelle la métrique de Aichelburg-Sexl. Il s'agit en gros de la forme que prend l'espace-temps autour d'un trou noir lorsque celui-ci est accéléré à une vitesse proche de celle de la lumière par rapport à un autre observateur au repos. Les calculs reposaient sur des approximations raisonnables mais pas à l'abri de toutes critiques et les résultats obtenus semblaient en accord avec la conjecture de Thorne. Comment savoir si une prise en compte plus rigoureuse de ce qui se passe lors d'une collision n'invaliderait pas les arguments avancés jusqu'ici en montrant que la formation d'un trou noir n'est pas possible ou pour le moins peu probable ?

Steven Giddings, ancien thésard d'Edward Witten et professeur à l'Université de Santa Barbara. Crédit : physics.ucsb.edu
Mettant à profit leurs compétence en relativité numériquenumérique, Matthew Choptuik, de l'Université de la Colombie-Britannique (Canada), et Frans Pretorius, de l'Université de Princeton, ont décidé d'en avoir le cœur net. Leur but a donc été de résoudre numériquement les équations d'Einstein avec le moins d'approximations possible et en plein régime non linéaire.
Ils ont tout de même approximé les particules par des étoilesétoiles bosoniques. Il s'agit en gros de champs de particules scalaires, plus simples que les fermionsfermions de la matière (comme les électronsélectrons et les quarksquarks) liés par leur propre champ de gravitation décrit par les équations d'Einstein. On obtient alors une solution similaire à celle d'une masse de fluide autogravitante représentant une étoile en relativité générale. Cette masse fluide peut se déformer et on n'est donc pas contraint de fixer arbitrairement la géométrie de l'espace-temps pour qu'elle soit celle de la solution de Schwarzschild modulo quelques perturbations linéaires.
Remarquablement, les calculs prenant en compte tous les détails de la dynamique de l'espace-temps lors de la collision ont montré que non seulement un horizon des événementshorizon des événements se formait bien mais qu'il fallait seulement un tiers de l'énergie associée à la masse de Planck pour qu'un mini trou noir apparaisse lors d'une collision entre particules.
On peut donc penser que le Tevatron a peut-être déjà exclu une masse de Planck inférieure à 5 TeV mais aussi que le LHC sera bel est bien capable de créer des trous noirs (et peut-être des trous de vers) en 2010 même si la masse de Planck est de l'ordre de 15 TeV !